






还剩21页未读,
继续阅读
成套系列资料,整套一键下载
人教A版数学高二选择性必修第三册 第八章 成对数据的统计分析 单元复习题 课件
展开
这是一份人教A版数学高二选择性必修第三册 第八章 成对数据的统计分析 单元复习题 课件,共29页。
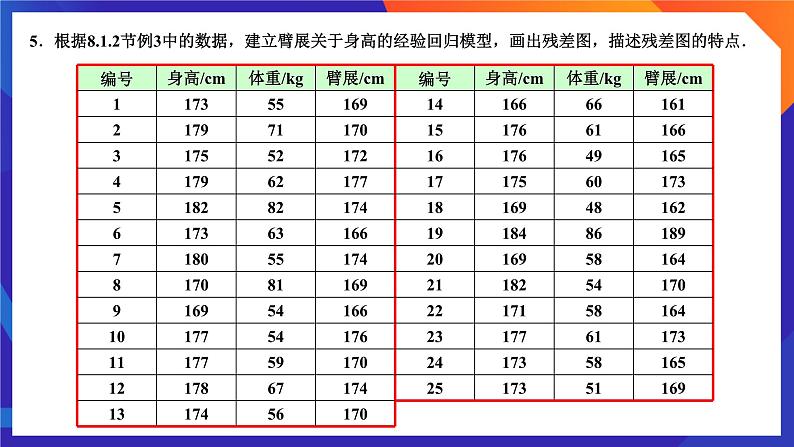
第八章 成对数据的统计分析 单元复习题1.变量x与y的观测数据的散点图如图所示,据此可以判断变量x与y之间( )A.很可能存在负相关 B.一定存在正相关C.很可能存在正相关 D.一定不存在负相关C复习参考题4. 8.3节例4中推断吸烟与患肺癌是有关联的,能用一元线性回归模型建立它们之间的关系吗?为什么?不能.因为吸烟和患肺癌是分类变量,一元线性回归模型主要是刻画数值变量之间的关系.观察吸烟和患肺癌的散点图可以发现,无论有多少个观测,在图中最多只有4个点,没有线性趋势.5.根据8.1.2节例3中的数据,建立臂展关于身高的经验回归模型,画出残差图,描述残差图的特点.身高/cm臂展/cm身高/cm残差/cm残差图中除身高为184 cm的观测(第19个观测),其他点大致均匀分布在横轴两侧,说明模型拟合较好.第19个观测的残差比较大,建议检查一下该数据在测量和记录过程中是否有误.6.下表是1896~2016年男子三级跳远奥运会冠军的成绩,请分析这组数据,能用一元线性回归模型刻画这组数据吗?年份成绩/m第6题(1)先画三级跳远成绩与年份之间的散点图,如图(1)所示.观察散点图,可以看到随着年份的增大,成绩有增加的趋势,因此可以考虑用一元线性回归模型刻画. 年份成绩/m第6题(2)年份残差/m第6题(3)7.车胎凹槽深度是影响汽车刹车的因素,汽车行驶会导致轮胎胎面磨损.某实验室通过试验测得行驶里程与某品牌轮胎凹槽深度的数据,请根据数据建立车胎凹槽深度和汽车行驶里程的关系,并解释模型的含义.轮胎凹槽深度/mm 行驶里程/万 km 第7题(2)先画轮胎凹槽深度与行驶里程之间的散点图,如图(1)所示.观察散点图,可以看到随着行驶里程的增加,轮胎凹橧深度有减小的趋势,因此可以考虑用一元线性回归模型建模. 残差/mm 行驶里程/万 km 第7题(3)该模型的决定系数为0.952,残差图如图(3)所示.从残差图可以看到,残差与行驶里程有非线性关系,因此考虑在模型中引入行驶里程的非线性变换.轮胎凹槽深度/mm 第7题(4)8.为考察某种药物预防疾病的效果,进行动物试验,得到如下列联表:单位:只 根据频率稳定于概率的原理,可以推断服用药物不患病的概率更大. 7.气象部门由每天的最高气温的数据,得到每月最高气温的平均数,简称平均高温.下表是2017年31个城市1月和7月的平均高温数据.(1)画出并观察各城市1月与7月的平均高温的散点图,你认为1月与7月的平均高温有线性趋势吗?描述散点图的特点.(1)先画7月的平均高温与1月的平均高温的散点图,如图(1)所示.观察散点图,可以看到部分城市1月的平均高温与7月的平均高温有线性趋势,但有些城市没有这个趋势.例如拉萨、西宁和贵阳三个城市7月的平均高温偏低,而1月的平均高温并不低;广州、海口和南宁三个城市1月的平均高温不低于20℃,是偏高的,但7月的平均高温并没有明显偏高;昆明7月与1月平均高温温差很小.1月平均高温/℃7月平均高温/℃第9题(2)(2)可以结合地理条件分析几个特殊的城市没有线性趋势的原因.去掉上述7个城市后,其余24个城市的散点图如图(2)所示.可以看到7月的平均高温随1月的平均高温增加有增加的趋势, 1月平均高温/℃7月平均高温/℃第9题(3)1月平均高温/℃残差/℃第9题(4)且残差图大致均匀分布在横轴两侧(图(4)),说明此时模型的拟合效果比较好.对于大部分城1月的平均高温越高,则同年7月的平均高温会越高.但是由于部分城市的地理位置和气候条件特殊,并不具有上述规律.课 程 结 束
第八章 成对数据的统计分析 单元复习题1.变量x与y的观测数据的散点图如图所示,据此可以判断变量x与y之间( )A.很可能存在负相关 B.一定存在正相关C.很可能存在正相关 D.一定不存在负相关C复习参考题4. 8.3节例4中推断吸烟与患肺癌是有关联的,能用一元线性回归模型建立它们之间的关系吗?为什么?不能.因为吸烟和患肺癌是分类变量,一元线性回归模型主要是刻画数值变量之间的关系.观察吸烟和患肺癌的散点图可以发现,无论有多少个观测,在图中最多只有4个点,没有线性趋势.5.根据8.1.2节例3中的数据,建立臂展关于身高的经验回归模型,画出残差图,描述残差图的特点.身高/cm臂展/cm身高/cm残差/cm残差图中除身高为184 cm的观测(第19个观测),其他点大致均匀分布在横轴两侧,说明模型拟合较好.第19个观测的残差比较大,建议检查一下该数据在测量和记录过程中是否有误.6.下表是1896~2016年男子三级跳远奥运会冠军的成绩,请分析这组数据,能用一元线性回归模型刻画这组数据吗?年份成绩/m第6题(1)先画三级跳远成绩与年份之间的散点图,如图(1)所示.观察散点图,可以看到随着年份的增大,成绩有增加的趋势,因此可以考虑用一元线性回归模型刻画. 年份成绩/m第6题(2)年份残差/m第6题(3)7.车胎凹槽深度是影响汽车刹车的因素,汽车行驶会导致轮胎胎面磨损.某实验室通过试验测得行驶里程与某品牌轮胎凹槽深度的数据,请根据数据建立车胎凹槽深度和汽车行驶里程的关系,并解释模型的含义.轮胎凹槽深度/mm 行驶里程/万 km 第7题(2)先画轮胎凹槽深度与行驶里程之间的散点图,如图(1)所示.观察散点图,可以看到随着行驶里程的增加,轮胎凹橧深度有减小的趋势,因此可以考虑用一元线性回归模型建模. 残差/mm 行驶里程/万 km 第7题(3)该模型的决定系数为0.952,残差图如图(3)所示.从残差图可以看到,残差与行驶里程有非线性关系,因此考虑在模型中引入行驶里程的非线性变换.轮胎凹槽深度/mm 第7题(4)8.为考察某种药物预防疾病的效果,进行动物试验,得到如下列联表:单位:只 根据频率稳定于概率的原理,可以推断服用药物不患病的概率更大. 7.气象部门由每天的最高气温的数据,得到每月最高气温的平均数,简称平均高温.下表是2017年31个城市1月和7月的平均高温数据.(1)画出并观察各城市1月与7月的平均高温的散点图,你认为1月与7月的平均高温有线性趋势吗?描述散点图的特点.(1)先画7月的平均高温与1月的平均高温的散点图,如图(1)所示.观察散点图,可以看到部分城市1月的平均高温与7月的平均高温有线性趋势,但有些城市没有这个趋势.例如拉萨、西宁和贵阳三个城市7月的平均高温偏低,而1月的平均高温并不低;广州、海口和南宁三个城市1月的平均高温不低于20℃,是偏高的,但7月的平均高温并没有明显偏高;昆明7月与1月平均高温温差很小.1月平均高温/℃7月平均高温/℃第9题(2)(2)可以结合地理条件分析几个特殊的城市没有线性趋势的原因.去掉上述7个城市后,其余24个城市的散点图如图(2)所示.可以看到7月的平均高温随1月的平均高温增加有增加的趋势, 1月平均高温/℃7月平均高温/℃第9题(3)1月平均高温/℃残差/℃第9题(4)且残差图大致均匀分布在横轴两侧(图(4)),说明此时模型的拟合效果比较好.对于大部分城1月的平均高温越高,则同年7月的平均高温会越高.但是由于部分城市的地理位置和气候条件特殊,并不具有上述规律.课 程 结 束
相关资料
更多









