2024中考复习之圆与相似综合导学案【专项训练】

这是一份2024中考复习之圆与相似综合导学案【专项训练】，共6页。试卷主要包含了用运动的观点看，切割线定理，如图，PAB等内容，欢迎下载使用。
相交弦定理、切割线定理、割线定理有着密切的联系，主要体现在：
1、用运动的观点看，切割线定理、割线定理是相交弦定理另一种形式，即移动圆内两条相交弦使其交点在圆上和圆外的情况；
2、从定理的证明方法看，都是由一对相似三角形得到的等积式，熟悉以下基本图形、基本结论：
基础知识检测
1、如图，⊙O的弦AB平分半径OC，交OC于P点，已知PA、PB的长分别为方程的两根，求此圆半径.
2、如图，在△ABC中，∠C=90°,AB=10，AC=6，以AC为直径作圆与斜边交于点P,求BP的长.
3、如图，PAB、PCD为⊙O的两条割线，若PA=5，AB=7，CD=11，求AC:BD的值.
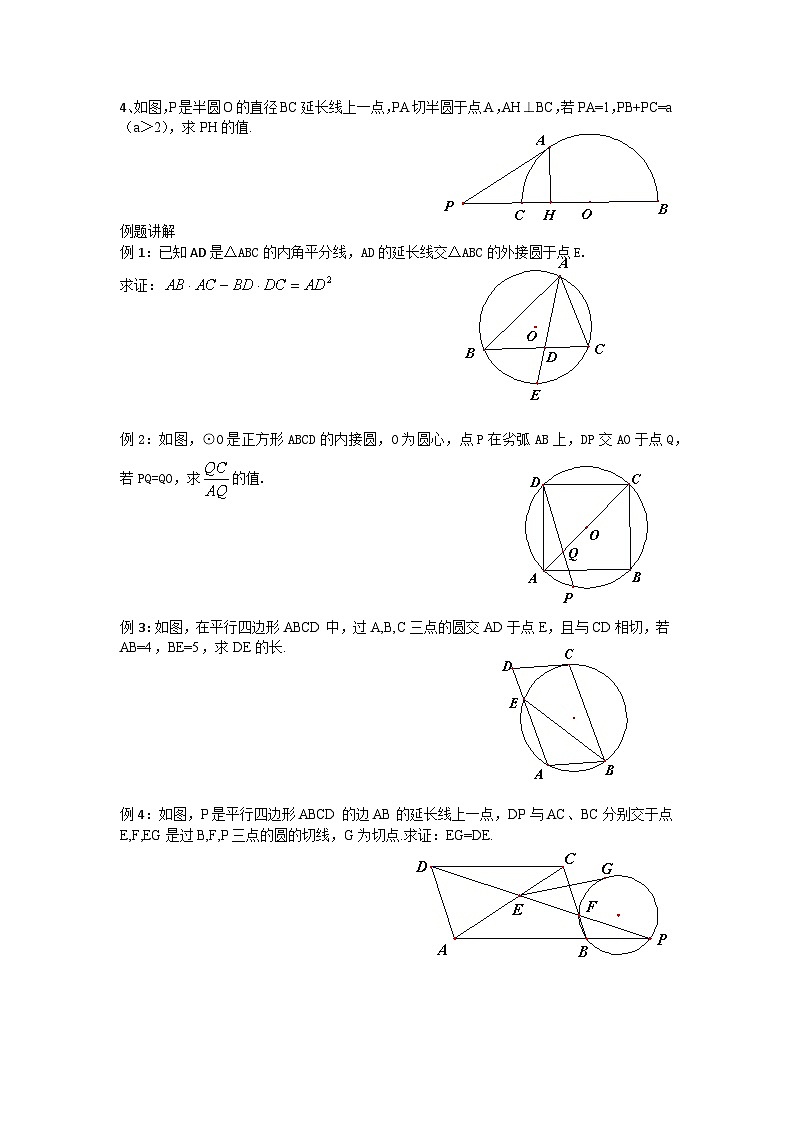
4、如图，P是半圆O的直径BC延长线上一点，PA切半圆于点A，AH⊥BC，若PA=1，PB+PC=a（a＞2），求PH的值.
例题讲解
例1：已知AD是△ABC的内角平分线，AD的延长线交△ABC的外接圆于点E.
求证：
例2：如图，⊙O是正方形ABCD的内接圆，O为圆心，点P在劣弧AB上，DP交AO于点Q，若PQ=QO，求的值.
例3：如图，在平行四边形ABCD中，过A,B,C三点的圆交AD于点E，且与CD相切，若AB=4，BE=5，求DE的长.
例4：如图，P是平行四边形ABCD的边AB的延长线上一点，DP与AC、BC分别交于点E,F,EG是过B,F,P三点的圆的切线，G为切点.求证：EG=DE.
例5：如图，设△ABC是直角三角形，点D在斜边BC上，D=4DC，一圆过点C,且与AC相交于F，与AB相切于AB中点G，求证：AD⊥BF.
例6：如图，△ABC内接于⊙O，AB是⊙O的直径，PA是过A点的直径，∠PAC=∠B.
（1）求证：PA是⊙O的切线；
（2）如果弦CD交AB于E,CD的延长线交PA于F，AC=8，CE:ED=6：5，AE:EB=2：3，求AB的长和∠ECB的正切值.
例7：已知，如图，ABCD为正方形，以D为圆心，AD为半径的圆弧与以BC为直径的⊙O相交于P,C两点，连接AC,AP,CP，并延长CP,AP分别交AB,BC、⊙O于E,H,F三点，连结OF.
（1）求证：△AEP∽△CEA；
（2）判断线段AB与OF的位置关系，并证明你的结论；
（3）求BH:HC.
例8：如图，P为⊙O外一点，过点P作⊙O的两条割线，分别交⊙O于A,B和C,D，且AB为⊙O的直径，已知PA=AO=2cm，，求PC的长.
例9：如图，等边△ABC中，边AB与⊙O相切于点H，边BC,CA分别与⊙O交于点D,
已知AG=2，GF=6，FC=1.求DE的值.
反馈练习
1、如图，△ABC是⊙O的内接正三角形，弦EF经过BC的中点D，且EF∥AB，若AB=2，求DE的长.
2、如图，已知A,B,C,D在同一个圆上，BC=CD,AC与BD交于E，若AC=8，CD=4，且线段BE、ED为正整数，求BD的值.
3、如图，AB是⊙O的直径，C是AB延长线上的一点，CD是⊙O的切线，D为切点，过点B做⊙O的切线交CD于点E，若AB=CD=2，求CE的值.
4、如图，BC是半圆⊙O的直径，EF⊥BC于点F，BF=5FC.已知AB=8，AE=2.求AD的长.
5、如图，在以O为圆心的两个同心圆中，MN为大圆的直径，交小圆于点P,Q，大圆的弦MC交小圆于点A,B，若OM=2，OP=1，MA=AB=BC，求△MBQ的面积.
6、如图，在△ABC中，AB＞AC，过点A作△ABC外接圆的切线，交BC延长线于点D，E为AD的中点，连接BE交△ABC外接圆于点F，求证：∠FAC=∠FDA.
7、如图，已知AB为⊙O的直径，C为⊙O上一点，延长BC至D，使CD=BC,CE⊥AD于E,BE交⊙O于F,AF交CE于P,求证：PE=PC.
8、如图，在△ABC中，以边BC为直径作半圆交边AB,AC于D,E两点，若DE=EC=4，,求的值.
9、如图，已知PA且⊙O于点A，割线PBC交⊙O于点B,C，PD⊥AB于点D，PD、AO的延长线相交于点E，连CE并延长交⊙O于点F，连AF.
（1）求证：△PBD∽△PEC；
（2）若AB=12，tan∠EAF=,求⊙O的半径长.