陕西省榆林市榆阳区2023-2024学年七年级下学期期末数学试题

这是一份陕西省榆林市榆阳区2023-2024学年七年级下学期期末数学试题，共8页。试卷主要包含了本试卷分为第一部分，领到试卷和答题卡后，请用0等内容，欢迎下载使用。
注意事项：
1.本试卷分为第一部分（选择题）和第二部分（非选择题）。全卷共4页，总分120分。考试时间120分钟。
2.领到试卷和答题卡后，请用0.5毫米黑色墨水签字笔，分别在试卷和答题卡上填写姓名和准考证号。
3.请在答题卡上各题的指定区域内作答，否则作答无效。
4.作图时，先用铅笔作图，再用规定签字笔描黑。
5.考试结束，本试卷和答题卡一并交回。
第一部分（选择题 共24分）
一、选择题（共8小题，每小题3分，计24分.每小题只有一个选项是符合题意的）
1.下列成语描述的事件是不可能事件的是
A.水滴石穿B.心想事成C.一步登天D.水涨船高
2.中华文明，源远流长；中华汉字，寓意深广.下列四个汉字中，可看作轴对称图形的是
A.B.C.D.
3.如图，已知，，若，则的度数为
A.B.C.D.
4.下列运算正确的是
A.B.
C.D.
5.地表以下岩层的温度（℃）与所处深度（km）有如下关系：
若地表以下岩层的温度是，估计该岩层所处的深度是
A.B.C.D.
6.如图，与关于所在直线对称，若，则的度数为
A.B.C.D.
7.与按如图所示方式放置，点、、、在同一条直线上，，，若要使得，则需要补充的条件可以是
A.B.C.D.
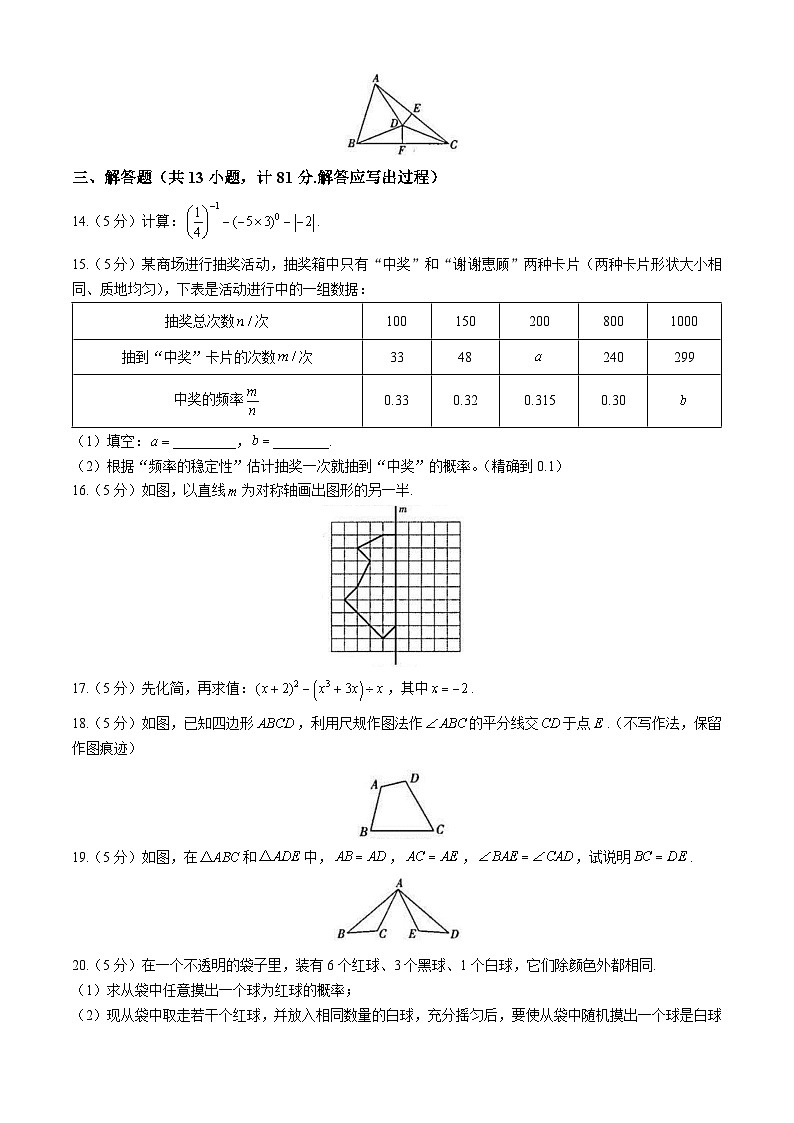
8.如图，在中，是边上的中线，是的高，若，，则的度数为
A.B.C.D.
第二部分（非选择题 共96分）
二、填空题（共5小题，每小题3分，计15分）
9.科学家发现，在一般光照条件下，每千克小球藻（鲜重）经光合作用每小时约可释放氧气0.00064千克.数据0.00064用科学记数法表示为____________.
10.在中，，，则的长可能为____________.（只写一个）
11.如图，在中，平分，于点，连接，若，，则的面积是________.
12.长方形一条边的长度为厘米，其周长为20厘米，面积为平方厘米，则与之间的关系可以表示为________.
13.如图，在中，、分别是、边的垂直平分线，连接、、，若，则的度数为________°.
三、解答题（共13小题，计81分.解答应写出过程）
14.（5分）计算：.
15.（5分）某商场进行抽奖活动，抽奖箱中只有“中奖”和“谢谢恵顾”两种卡片（两种卡片形状大小相同、质地均匀），下表是活动进行中的一组数据：
（1）填空：_________，________.
（2）根据“频率的稳定性”估计抽奖一次就抽到“中奖”的概率。（精确到0.1）
16.（5分）如图，以直线为对称轴画出图形的另一半.
17.（5分）先化简，再求值：，其中.
18.（5分）如图，已知四边形，利用尺规作图法作的平分线交于点.（不写作法，保留作图痕迹）
19.（5分）如图，在和中，，，，试说明.
20.（5分）在一个不透明的袋子里，装有6个红球、3个黑球、1个白球，它们除颜色外都相同.
（1）求从袋中任意摸出一个球为红球的概率；
（2）现从袋中取走若干个红球，并放入相同数量的白球，充分摇匀后，要使从袋中随机摸出一个球是白球的概率是，则取走了多少个红球？
21.（6分）如图，小明家住在河岸边的处，河对岸的处有一棵树，他想要测得这棵树与自己家之间的距离.设计了下面的方案：在与点同侧的河岸边选择一点，测得，，然后在处立了标杆，使，，此时测得的长就是，两点间的距离.小明设计的方案是否正确？请说明理由.
22.（7分）如图，直线、交于点，，射线将分成两个角，.
（1）求的度数；
（2）若，且射线在内部，求的度数.
23.（7分）如图是一个长方形纸片，它的长为，宽为，现用剪刀在长方形纸片内剪的去2个边长均为的正方形.
（1）用含，的代数式表示剩余纸片的面积；（结果化为最简形式）
（2）若，，求剩余纸片的面积.
24.（8分）如图，在四边形中，经过点的直线交于点，且，.
（1）试说明；
（2）的平分线与的平分线交于点，若，，求的度数.
25.（8分）大自然中的大部分物质具有热胀冷缩现象，而水则具有反膨胀现象，如图所示是当温度在时，水的密度（单位：）随着温度（单位：℃）的变化关系图象.
根据图象解答下列问题：
（1）在这个变化过程中，自变量是________，因变量是________；
（2）图中点表示的意义题什么？
（3）在范围内，当温度为多少℃时，水的密度为？
（4）当温度在变化时，随着温度增大，水的密度是如何变化的？
26.（10分）【问题背景】
在中，，，点为边上的动点，连接，作且，过点作于点.
【问题探究】
（1）如图1，试说明；
（2）如图2，连接交于点，若，试说明点是的中点.
榆阳区2023～2024学年度第二学期期末质量检测
七年级数学试题参考答案及评分标准
一、选择题（共8小题，每小题3分，计24分.每小题只在一个选项是符合题意的）
1.C 2.B 3.A 4.D 5.B 6.A 7.D 8.C
二、填空题（共5小题，每小题3分，计15分）
9. 10.8（答案不唯一，大于6且小于10的数均正确）
11.18 12.（其他形式正确也可） 13.50
三、解答题（共13小题，计81分.解答应写出过程）
14.解：原式 （3分） .（5分）
15.解：（1）63，0.299.（4分）
（2）估计抽奖一次就抽到“中奖”的概率是0.3.（5分）
16.解：如图所示.
（5分）
17.解：原式（2分）
，（4分）
当时，原式.（5分）
18.解：如图所示，即为所求.
（5分）
19.解：因为，所以，即.（2分）
在和中，因为，，，
所以，（4分）所以.（5分）
20.解：（1）从袋中任意摸出一个球有10种等可拕结果，其中是红球的有6种结果，
所以从袋中任意摸出一个球为红球的概率为.（2分）
（2）由题意可得袋中球的总数不变，设取走了个红球，则放入了个白球，
根据题意，得，（4分）
解得，所以取走了3个红球.（5分）
21.解：小明设计的方案正确.（1分）
理由：在和中，
，，，
所以，（4分）
所以，故的长就是，两点间的距离.（6分）
22.解：（1）因为，所以.（2分）
因为，，所以，（3分）
所以.（4分）
（2）因为，所以，（5分）
所以，（6分）所以.（7分）
23.解：（1）由题意可得（2分）
，
所以剩余纸片的面积为.（4分）
（2）若，，（5分），
所以剩余纸片的面积为.（7分）
24.解：（1）因为，所以.（1分）
因为，所以，（2分）
所以.（3分）
（2）因为，所以，.（5分）
因为平分，所以.（6分）
因为，平分，所以，（7分）
所以.（8分）
25.解：（1）温度，水的密度.（2分）
（2）当时，水的密度为.（说法不唯一，合理即可）（4分）
（3）当温度为时，水的密度为.（6分）
（4）由图可知，当温度在时，水的密度逐渐增大；（7分）
当温度在时，水的密度逐渐减小.（8分）
26.解：（1）因为，所以.（1分）
因为，，所以，，所以.（3分）
在和中，，，，
所以，（4分）所以.（5分）
（2）因为，，所以.（6分）
在和中，，，，所以（AAS），（7分）所以，所以.（8分）
因为，所以，即点是的中点.（9分）
由（1）可知，所以，则，所以点是的中点.（10分）
深度/km
1
2
3
4
5
…
温度/℃
55
90
125
160
195
…
抽奖总次数次
100
150
200
800
1000
抽到“中奖”卡片的次数次
33
48
240
299
中奖的频率
0.33
0.32
0.315
0.30