数学3.3 整式教课课件ppt

这是一份数学3.3 整式教课课件ppt，共30页。PPT课件主要包含了课前预习，典例讲练，三棱柱，四棱柱，五棱柱，六棱柱，n＋4，观察下列等式，n2＋n＋1等内容，欢迎下载使用。

数学 七年级上册 BS版
通过题目给出的有限个数、式或图形等，从这些简单的、 局部的、特殊的情形出发，经过观察、对比、提炼，寻找共同 点，发现隐藏的规律，并归纳得到数学结论，从而解决问题.因 此，归纳是发现数规律与结论，解决数学问题的一种重要策略.
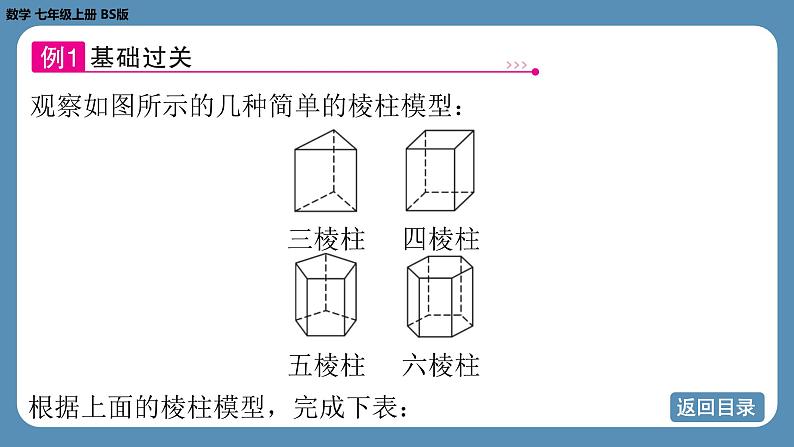
观察如图所示的几种简单的棱柱模型：
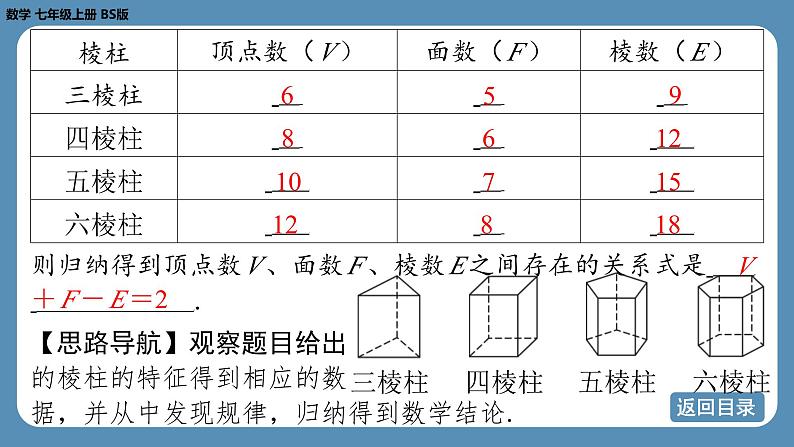
根据上面的棱柱模型，完成下表：
则归纳得到顶点数 V 、面数 F 、棱数 E 之间存在的关系式是 ⁠ ⁠.
＋ F － E ＝2　
【思路导航】观察题目给出的棱柱的特征得到相应的数据，并从中发现规律，归纳得到数学结论.
【解析】三棱柱：6，5，9→6＋5－9＝2；四棱柱：8，6， 12→8＋6－12＝2；五棱柱：10，7，15→10＋7－15＝2；六棱 柱：12，8，18→12＋8－18＝2.对比、分析得到的数据，发现 顶点数加上面数减去棱数等于定值2这一规律，于是归纳得到数 学结论为 V ＋ F － E ＝2，故答案为6，5，9；8，6，12；10， 7，15；12，8，18； V ＋ F － E ＝2.
【点拨】通过观察三棱柱、四棱柱、五棱柱、六棱柱几个特殊 图形的特征得到相关数据，再对比、分析，从中发现具有一般 性的规律：顶点数＋面数－棱数＝2.本例充分体现了数学中的 归纳思想和方法，使我们认识了这一数学问题的本质，总结出 数学公式.因为 n （ n ≥3）棱柱有2 n 个顶点，3 n 条棱，（ n ＋ 2）个面，所以2 n ＋（ n ＋2）－3 n ＝3 n －2－3 n ＝2，即顶点数 ＋面数－棱数＝2.
若用大小相同的小三角形摆成如图所示的图形，按照这样的规 律摆放，则第 n （ n 为正整数）个图形中所有小三角形的个数 是 ⁠.
【解析】当 n ＝1时，图中小三角形的个数为3×2－3＋4＝7； 当 n ＝2时，图中小三角形的个数为3×3－3＋4＝10；当 n ＝3 时，图中小三角形的个数为3×4－3＋4＝13；当 n ＝4时，图中 小三角形的个数为3×5－3＋4＝16；因此，第 n 个图形中所有 小三角形的个数为3（ n ＋1）－3＋4＝3 n ＋3－3＋4＝3 n ＋4. 故答案为3 n ＋4.
利用归纳策略，解答下列问题：
（1）按照以上规律写出第5个等式：
（3）求 a1＋ a2＋ a3＋…＋ a20的值.
【思路导航】观察给出的4个等式的特征，通过对比、分析、提 炼，从中发现这些等式的共同点和变化规律，归纳总结得到数 学结论，并利用数学结论，就能顺利地解决问题.
【点拨】从本例的解答过程看出，利用归纳策略解答问题的一 般过程：（1）观察题目给出简单的、局部的、特殊的有限个 数、式或图形等的特性；（2）通过对比、分析、提炼寻找它们 之间的共同点，发现隐藏其中的变化规律；（3）根据掌握的变 化规律，进行大胆的猜想，归纳得到数学结论；（4）验证归纳 得到的数学结论的正确性，并利用它去解决数学问题.
观察下列由连续的正整数组成的宝塔形等式：1＋2＝3；4＋5＋6＝7＋8；9＋10＋11＋12＝13＋14＋15；16＋17＋18＋19＋20＝21＋22＋23＋24；……
（1）第6层等号右侧的第一个数是 ，第 n 层等号右侧的 第一个数是 （用含 n 的式子表示， n 是正整数）；
（1）【解析】观察发现：第6层等号左侧的第一个数是62＝ 36，第 n 层等号左侧的第一个数是 n2；第6层等号右侧的第一个 数是36＋6＋1＝43，第 n 层等号右侧的第一个数是 n2＋ n ＋1.故 答案为43， n2＋ n ＋1.
（2）求第19层等号右侧最后三个数的和.
（2）解：由题意知，第19层等号右侧最后三个数分别为202－ 1，202－2，202－3，所以第19层等号右侧最后三个数的和为 （202－1）＋（202－2）＋（202－3）＝3×400－6＝1194.
毕达哥拉斯学派对“数”与“形”的巧妙结合作了如下研究：
（1）请在表格中写出第6层各个图形的几何点数，并归纳出第 n 层各个图形的几何点数；【思路导航】（1）观察题目给出的四幅图形，找出对应的每一 层的几何点数，寻找数字间的变化规律，便能写出第6层各个图 形的几何点数，并以此归纳出一般情况，即得到第 n 层各个图 形的几何点数；
（1）【解析】因为前3层三角形数的几何点数分别是1，2，3，所以第6层的几何点数是6，第 n 层的几何点数是 n .因为前3层正方形的几何点数分别是1＝2×1－1，3＝2×2－1， 5＝2×3－1，所以第6层的几何点数是2×6－1＝11，第 n 层的几何点数是2 n －1.因为前3层五边形的几何点数分别是1＝3×1－2，4＝3×2－2， 7＝3×3－2，
所以第6层的几何点数是3×6－2＝16，第 n 层的几何点数是3 n －2.因为前3层六边形的几何点数分别是1＝4×1－3，5＝4×2－3， 9＝4×3－3，所以第6层的几何点数是4×6－3＝21，第 n 层的几何点数是4 n －3.故答案为6，11，16，21， n ，2 n －1，3 n －2，4 n －3.
（2）求第100层各个图形的几何点数的总和.【思路导航】（2）利用得到的数学结论，就能求出第100层 各个图形的几何点数的总和.
（2）解：当 n ＝100时，则第100层各个图形的几何点数的总和为　 n ＋（2 n －1）＋（3 n －2）＋（4 n －3）＝10 n －6＝10×100－6＝994.
【点拨】利用归纳得到数学结论这类问题，常常都与自然数 n 有关联.在对题目给出的有限个数、式或图形等进行观察、对 比、分析时，要密切注意与自然数 n 的联系，并要重点关注自 然数 n 引起其余部分的变化，从中寻找共同点，发现隐藏的规 律，揭示问题的本质，归纳得到数学结论.
某类碳氢化合物中前6种化合物的分子结构模型如图所示，其中 灰球代表碳原子，白球代表氢原子.按照这一规律，请利用归纳 策略解答下列问题：（1）第 n （ n 为正整数）种化合物的分子结构模型中有 ⁠ 个氢原子；
（1）【解析】由图可知，第1种化合物中氢原子的个数为4＝ 2×1＋2；第2种化合物中氢原子的个数为6＝2×2＋2；第3种化合物中氢原子的个数为8＝2×3＋2；第4种化合物中氢原子的个数为10＝2×4＋2；第5种化合物中氢原子的个数为12＝2×5＋2；第6种化合物中氢原子的个数为14＝2×6＋2，所以第 n （ n 为正整数）种化合物中氢原子的个数为（2 n ＋2）.故答案为（2 n ＋2）.
（2）第50种化合物的分子结构模型中有多少个氢原子？
（2）解：当 n ＝50时，2 n ＋2＝2×50＋2＝102.故第50种化合物的分子结构模型中有102个氢原子.