数学七年级上册第三章 整式及其加减3.3 整式课文配套ppt课件

这是一份数学七年级上册第三章 整式及其加减3.3 整式课文配套ppt课件，共29页。PPT课件主要包含了A级基础训练，B级能力训练，C级拓展训练等内容，欢迎下载使用。

数学 九年级上册 BS版
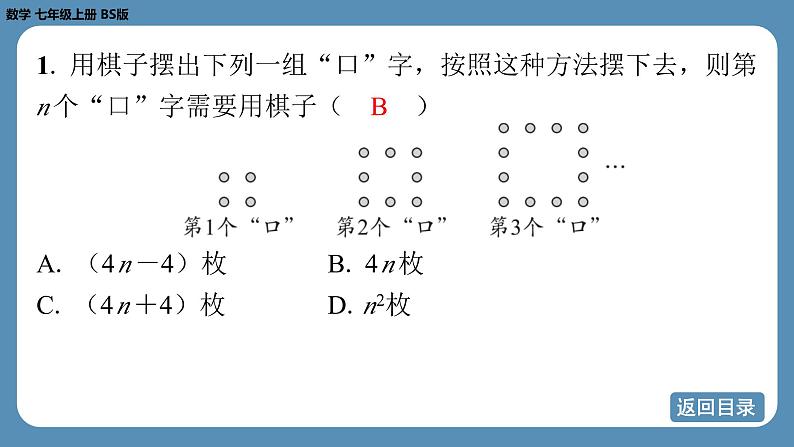
1. 用棋子摆出下列一组“口”字，按照这种方法摆下去，则第 n 个“口”字需要用棋子（　B　）
2. 观察下列算式：21＝2，22＝4，23＝8，24＝16，25＝32，26 ＝64，27＝128，28＝256……根据上述算式中的规律，你认为22 024的末位数字是（　D　）
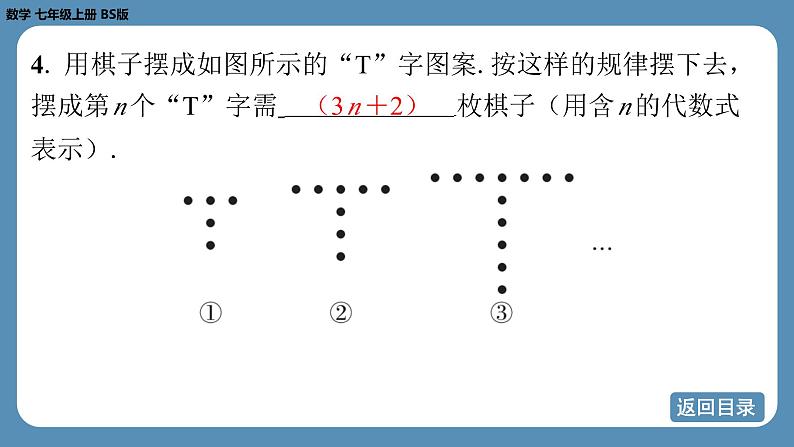
4. 用棋子摆成如图所示的“T”字图案.按这样的规律摆下去， 摆成第 n 个“T”字需 枚棋子（用含 n 的代数式 表示）.
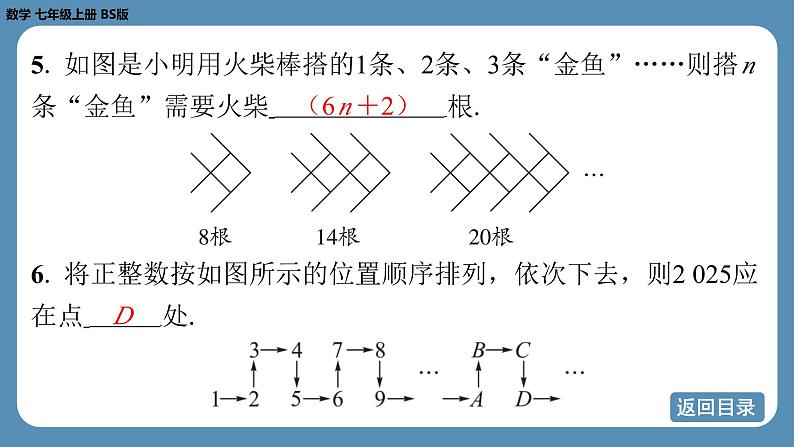
5. 如图是小明用火柴棒搭的1条、2条、3条“金鱼”……则搭 n 条“金鱼”需要火柴 根.
6. 将正整数按如图所示的位置顺序排列，依次下去，则2 025应 在点 处.
7. 你能比较20232024和20242023的大小吗？为了解决这个问题，我们先把它抽象成数学问题，写出它的一 般形式，即比较 nn＋1和（ n ＋1） n 的大小（ n 为正整数）.我们 从 n ＝1，2，3，…这些简单的情况入手，从中发现规律，经过 归纳，猜出结论.（1）通过计算，比较下列各组数字大小：①12 21；②23 32；③34 43；④45 54；⑤56 65；⑥67 76.
（1）【解析】通过计算得出，12＜21，23＜32，34＞43，45＞ 54，56＞65，67＞76.故答案为＜，＜，＞，＞，＞，＞.
（填“＞”“＜”或“＝”）
（2）将第（1）题的结果进行归纳，你能得出什么结论？（3）根据上面得到的结论，试比较两个数的大小： 20232024 20242023（填“＞”“＜”或“＝”）.
（2）解：由（1）的结果可知，当 n ≤2时， nn＋1＜（ n ＋1） n ；当 n ＞2时， nn＋1＞（ n ＋1） n .（ n 为正整数）
（3）【解析】根据以上结论得出，20232024＞20242023.故答案为 ＞.
8. 某餐厅中，一张桌子可以坐6人，如果把多张桌子摆在一 起，可以有以下两种摆放方式：
第一种方式：
第一种方式：
（1）当有5张桌子时，第一种摆放方式能坐 人，第二种 摆放方式能坐 人；（用含 n 的代数式表示）
（1）【解析】当有5张桌子时，第一种摆放方式能坐4×5＋2＝ 22（人），第二种摆放方式能坐2×5＋4＝14（人）.故答案为22，14.
（2）当有 n 张桌子时，第一种摆放方式能坐 ⁠ 人，第二种摆放方式能坐 人；
（2）【解析】第一种摆放方式中，只有一张桌子时，能坐6 人，后边多一张桌子能多坐4人，所以有 n 张桌子时，能坐6＋4（ n －1）＝（4 n ＋2）人；第二种中摆放方式，只有一张桌子时，能坐6人，后边多一张桌 子能多坐2人，所以有 n 张桌子时，能坐6＋2（ n －1）＝（2 n ＋4）人.故答案为（4 n ＋2），（2 n ＋4）.
（3）一天中午餐厅要接待98位顾客共同就餐（即桌子要摆在一 起），但餐厅只有25张这样的餐桌，若你是这个餐厅的经理， 你打算选择哪种方式来摆放餐桌？为什么？
（3）解：若我是这个餐厅的经理，我打算选择第一种摆放方式 来摆放餐桌.理由如下：因为当 n ＝25时，选择第一种摆放方式能坐4×25＋2＝102（人）＞98（人）；选择第二种摆放方式能坐2×25＋4＝54（人）＜98（人），所以选用第一种摆放方式才能坐下.
10. 已知一列数 a1， a2， a3，…， an 中任意三个相邻数之积都是 123.若 a100＝1， a2 000＝3，则 a300＝ ⁠.
【解答】由任意三个相邻数之积都是123可知， a1· a2· a3＝123， a2· a3· a4＝123， a3· a4· a5＝123，…， an · an＋1· an＋2＝123，可以推出 a1＝ a4＝ a7＝…＝ a3 n－2， a2＝ a5＝ a8＝…＝ a3 n－1， a3＝ a6＝ a9＝…＝ a3 n .
所以 a299＝ a2 000＝3， a301＝ a100＝1.因为 a299· a300· a301＝123，所以 a300＝123÷3＝41.故答案为41.
11. 我们把正六边形的顶点及其对称中心称作如图1所示基本图 的特征点，显然这样的基本图共有7个特征点，将此基本图不断 复制并平移，使得相邻两个基本图的一边重合，这样得到图2， 图3……
（1）观察以上图形并完成表格：
（1）【解析】观察图可知，图2中，有12个特征点；图3中，有17个特征点；图4中，有22个特征点.故答案为12，17，22.
（2）猜想：在图 n 中，有多少个特征点？（用含 n 的代数式 表示）
（2）解：结合图形和（1）可知，第一个图形有7个特征点，后面图形数每增加1个，特征点增 加5个，所以图 n 中，特征点个数为7＋（ n －1）×5＝5 n ＋2.
12. （选做）一个四位正整数 M ，如果 M 满足各个数位上的数 字均不为0，且它的千位数字与个位数字之和等于百位数字与十 位数字之和，那么称这个数 M 为“行知数”.例如： M1＝ 7643，因为7＋3＝6＋4，所以7643是“行知数”； M2＝6452， 因为6＋2≠4＋5，所以6452不是“行知数”.
（1）判断3524，1356是否为“行知数”？请说明理由.
解：（1）因为3＋4＝5＋2，所以3524是“行知数”.因为1＋6≠3＋5，所以1356不是“行知数”.
（2）若 N ＝1000 x ＋500＋10 y ＋7（其中1≤ x ≤9，1≤ y ≤9， 且 x ， y 都为整数）是“行知数”，且能被3整除，求满足条件 的所有 N 的值.
解：（2）因为 N ＝1000 x ＋500＋10 y ＋7（其中1≤ x ≤9，1≤ y ≤9，且 x ， y 都为整数）是“行知数”，所以 x ＋7＝5＋ y ，即 y － x ＝2.因为 M ＝1000 x ＋500＋10 y ＋7能被3整除，且 x ＋5＋ y ＋7＝ x ＋ y ＋12，所以 x ＋ y 能被3整除.当 x ＝1， y ＝3时， x ＋ y 不能被3整除，不符合题意；
当 x ＝2， y ＝4时， x ＋ y 能被3整除，符合题意，此时 N ＝2547；当 x ＝3， y ＝5时， x ＋ y 不能被3整除，不符合题意；当 x ＝4， y ＝6时， x ＋ y 不能被3整除，不符合题意；当 x ＝5， y ＝7时， x ＋ y 能被3整除，符合题意，此时 N ＝5577；当 x ＝6， y ＝8时，
x ＋ y 不能被3整除，不符合题意；当 x ＝7， y ＝9时， x ＋ y 不能被3整除，不符合题意.故满足条件的所有 N 的值有2547，5577.