初中北师大版4.3 角教学演示ppt课件

这是一份初中北师大版4.3 角教学演示ppt课件，共36页。PPT课件主要包含了典例讲练等内容，欢迎下载使用。
数学 七年级上册 BS版
◎问题综述　　线段与角是几何图形中的基本图形，掌握好线段和角的有 关计算问题是以后学习其他几何知识的基础.在进行线段和角的 有关计算中，经常用到分类讨论思想和方程思想，解答这类问 题时，一定要数形结合，分类做到不重不漏.
类型一　线段、角的和、差、倍、分问题
（1）如图，已知点 A ， B ， C ， D 在同一条直线上，点 D 是线段 AC 的中点，且 CB ＝5， AD ＝3，求线段 DC 及 AB 的长.
【思路导航】先根据中点的性质求出 DC ，再结合图形将线段相 加得到 AB 的长.
解：因为点 D 是线段 AC 的中点， AD ＝3，所以 DC ＝ AD ＝3， AC ＝2 AD ＝6.所以 AB ＝ AC ＋ CB ＝6＋5＝11.
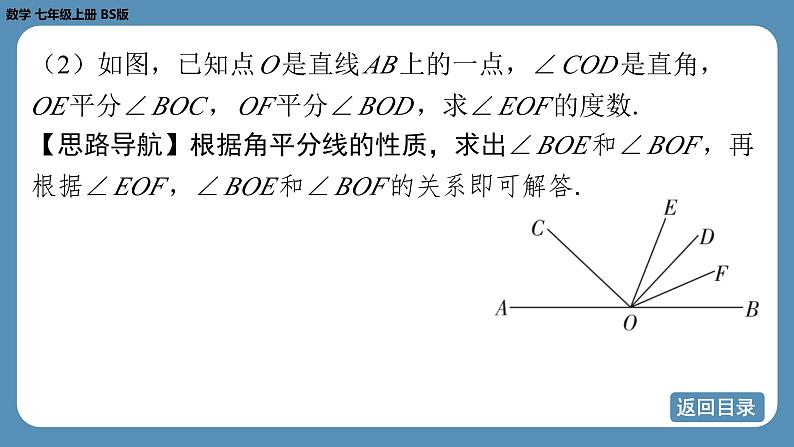
（2）如图，已知点 O 是直线 AB 上的一点，∠ COD 是直角， OE 平分∠ BOC ， OF 平分∠ BOD ，求∠ EOF 的度数.
【思路导航】根据角平分线的性质，求出∠ BOE 和∠ BOF ，再 根据∠ EOF ，∠ BOE 和∠ BOF 的关系即可解答.
【点拨】在进行线段长度和角度大小的计算时，关键是根据图 形和已知条件灵活地运用和、差、倍、分关系进行代换，逐步 向已知条件靠拢，注意线段的中点和角平分线的性质的应用.
1. 如图，已知∠ AOB ＝30°，∠ BOC ＝20°， OC 平分∠ AOD ，求∠ BOD 的度数.
解：因为∠ AOB ＝30°，∠ BOC ＝20°，所以∠ AOC ＝∠ AOB ＋∠ BOC ＝30°＋20°＝50°.因为 OC 平分∠ AOD ，所以∠ COD ＝∠ AOC ＝50°.所以∠ BOD ＝∠ BOC ＋∠ COD ＝20°＋50°＝70°.
类型二　线段、角中的整体代入思想
如图，已知点 C ， D 为线段 AB 上的两点（点 C 在点 D 左 侧），点 M ， N 分别为 AC ， BD 的中点， AB ＝12， CD ＝5.
（1）求线段 AC 与 DB 的长度的和；
【思路导航】（1）根据线段长度的和差，即可求出 AC ＋ DB ；
解：（1）根据题意，得 AC ＋ DB ＝ AB － CD ＝7.
（2）求线段 MN 的长.
【思路导航】（2）由（1）的结果结合线段的中点的性质，可得 MC ＋ ND ，再根据线段长度的和差即可解答.
【点拨】在求线段时，若某些线段不易求得，可考虑整体代入 思想的运用.
如图，已知射线 OA ， OB 分别为∠ MOP 和∠ NOP 的平分线， 且∠ MON ＝α，∠ NOP ＝β（β＜α），求∠ AOB 的大小.
类型三　线段、角中的方程思想
如图，已知点 E 是线段 AB 的中点，点 C 是 EB 上一点， AC ＝12.
（1）若 EC ∶ CB ＝1∶2，求 AB 的长；
【思路导航】（1）设 EC ＝ x ，根据比例关系，表示出 CB 的长 度，再根据题意列出方程即可求解；
解：（1）因为 EC ∶ CB ＝1∶2，所以可设 EC ＝ x ， CB ＝2 x .因为点 E 是线段 AB 的中点，所以 AE ＝ BE ＝ EC ＋ CB ＝ x ＋2 x ＝3 x .所以 AC ＝ AE ＋ EC ＝3 x ＋ x ＝12，解得 x ＝3.故 AB ＝2 AE ＝6 x ＝6×3＝18.
（2）若点 F 为 CB 的中点，求 EF 长.
【思路导航】（2）设 EC ＝ y ，根据题意，用含 y 的代数式表示出 CF 的长度，即可求解.
【点拨】当已知条件中数据较少，且知道线段之间的比例关系 或倍数关系时，可考虑设未知数，列方程进行求解.
1. 如图，已知∠ AOB ，∠ BOC ，∠ COD 的度数之比是 2∶1∶3，且∠ AOC ＋∠ BOD ＝140°，求∠ AOD 的度数.
解：设∠ BOC ＝ x ，则∠ AOB ＝2 x ，∠ COD ＝3 x .根据题意，得（2 x ＋ x ）＋（ x ＋3 x ）＝140°.
解得 x ＝20°.则∠ AOD ＝∠ AOB ＋∠ BOC ＋∠ COD ＝2 x ＋ x ＋3 x ＝6 x ＝6×20°＝120°.
类型四　线段、角中的分类讨论思想
已知两根木条，一根长20cm，另一根长24cm，将它们一端 重合且放在同一条直线上（不计木条粗细），则此时两根木条 的中点之间的距离为 ⁠.
【思路导航】画出草图，然后分木条的另一端在同一方向和不 在同一方向两种情况进行讨论.
【解析】设较长的木条为 AB ＝24cm，较短的木条为 BC ＝ 20cm，点 M ， N 分别为 AB ， BC 的中点，所以 BM ＝12cm， BN ＝10cm.如图1，当 BC 不在 AB 上时， MN ＝ BM ＋ BN ＝12＋10 ＝22（cm）；如图2，当 BC 在 AB 上时， MN ＝ BM － BN ＝12－ 10＝2（cm）.综上所述，两根木条的中点间的距离是2cm或 22cm.故答案为2cm或22cm.
【点拨】这类题一般没有给出配图，所以解题时需要自己根据 题意画出示意图.画图时，要注意线段的端点的位置或角的一边 的位置，根据可能的情况画图分类讨论进行解答.
1. 在同一平面内，已知∠ AOB ＝50°，∠ COB ＝30°，则∠ AOC 等于（　C　）
2. 已知线段 AB ，在直线 AB 上取一点 C ，使 AC ＝2 BC ，在 AB 的反向延长线上取一点 D ，使 DA ＝2 AB ，求 AC ∶ DB 的值.
解：设 BC ＝ x .因为 AC ＝2 BC ，所以 AC ＝2 x .
①如图1，当点 C 在线段 AB 上时，
AB ＝ AC ＋ BC ＝3 x .
因为 AD ＝2 AB ，所以 AD ＝6 x .
所以 BD ＝ AD ＋ AB ＝9 x .
②如图2，当点 C 在线段 AB 的延长线上时，
AB ＝ AC － BC ＝ x .
因为 AD ＝2 AB ，所以 AD ＝2 x .
所以 BD ＝ AD ＋ AB ＝3 x .
类型五　线段、角中的动态问题
已知∠ AOD ＝40°，射线 OC 从 OD 出发，绕点 O 以每秒 20°的速度按逆时针方向旋转，旋转时间为 t 秒（ t ≤7），射线 OE ， OF 分别平分∠ AOC 和∠ AOD .
（1）如图1，若 t ＝4，求∠ AOE 的度数；
【思路导航】（1）根据角平分线的过程即可求解；
（2）如图1，求∠ EOF 的度数（用含 t 的代数式表示）；
【思路导航】（2）根据旋转的过程和角平分线的定义进行计算即可；
【思路导航】（3）分两种情况讨论： OB 落在不同位置时进行角的计算即可求解.
①如图2，当 OB 落在 OF 和 OD 之间时，∠ BOD ＝∠ AOD －∠ AOB ＝40°－10 t °，所以40－10 t ＝10，解得 t ＝3.
②如图3，当 OB 落在 OD 和 OE 之间时，∠ BOD ＝∠ AOB －∠ AOD ＝10 t °－40°，
所以10 t －40＝10，解得 t ＝5.
【点拨】本题考查了角的计算、角的平分线的定义，解决本题 的关键是准确进行角的计算.
【新知理解】如图1，点 C 在线段 AB 上，图中共有 AB ， AC 和 BC 三条线段.若其中有一条线段的长度是另外一条线段长度的2 倍，则称点 C 是线段 AB 的“巧点”.（1）线段的中点 这条线段的“巧点”（填“是”或“不 是”）；
（1）【解析】如图，当点 C 是线段 AB 的中点，则 AB ＝2 AC ， 所以线段的中点是这条线段的“巧点”.故答案为是.
（2）若 AB ＝12cm，点 C 是线段 AB 的“巧点”，则 AC ＝ ⁠ cm.
【解决问题】（3）如图2，已知 AB ＝12cm.动点 P 从点 A 出发，以2cm/s的速 度沿 AB 向点 B 匀速移动；点 Q 从点 B 出发，以1cm/s的速度沿 BA 向点 A 匀速移动，点 P ， Q 同时出发，当其中一点到达终点 时，运动停止，设移动的时间为 t （s）.当 t 为何值时， A ， P ， Q 三点中一点恰好是以另外两点为端点的线段的“巧点”？