人教A版普通高中数学一轮复习第八章第七节抛物线学案

这是一份人教A版普通高中数学一轮复习第八章第七节抛物线学案，共23页。学案主要包含了常用结论等内容，欢迎下载使用。
2．了解抛物线的简单几何性质．
自查自测
知识点一 抛物线的定义
1．(教材改编题)动点P(x，y)到点F(3，0)的距离比它到直线x＋2＝0的距离大1，则动点P的轨迹是( )
A．椭圆B．双曲线
C．双曲线的一支D．抛物线
D 解析：因为动点P到点F(3，0)的距离比它到直线x＝－2的距离大1，所以将动点P到点F(3，0)的距离等于它到直线x＝－3的距离，因此动点P的轨迹是以(3，0)为焦点，x＝－3为准线的抛物线．
2．已知抛物线y2＝8px(p＞0)，F是焦点，则p表示( )
A．F到准线的距离B．F到准线距离的14
C．F到准线距离的18D．F到y轴的距离
B 解析：根据抛物线方程可知准线方程为x＝－2p，焦点F(2p，0)，所以焦点F到准线的距离为4p，则p表示F到准线距离的14．
核心回扣
1．我们把平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线．点F叫做抛物线的焦点，直线l叫做抛物线的准线．
2．当点F在直线l上时，与定点F和直线l距离相等的点的轨迹是过点F与直线l垂直的直线．
自查自测
知识点二 抛物线的标准方程及几何性质
1．判断下列说法的正误，正确的打“√”，错误的打“×”．
(1)方程y＝4x2表示焦点在x轴上的抛物线，焦点坐标为(1，0)．( × )
(2)抛物线既是中心对称图形，又是轴对称图形．( × )
(3)以(0，1)为焦点的抛物线的标准方程为x2＝4y.( √ )
2．(教材改编题)抛物线x2＝14y的准线方程为( )
A．y＝－116B．x＝－116
C．y＝116D．x＝116
A 解析：由抛物线的标准方程，可得抛物线的焦点位于y轴正半轴上，焦点坐标为0，116，准线方程为y＝－116．
3．(多选题)过点P(－2，3)的抛物线的标准方程可以是( )
A．y2＝－92xB．y2＝92x
C．x2＝－43yD．x2＝43y
AD 解析：设抛物线的标准方程为y2＝kx或x2＝my，代入点P(－2，3)，解得k＝－92，m＝43，所以y2＝－92x或x2＝43y.
核心回扣
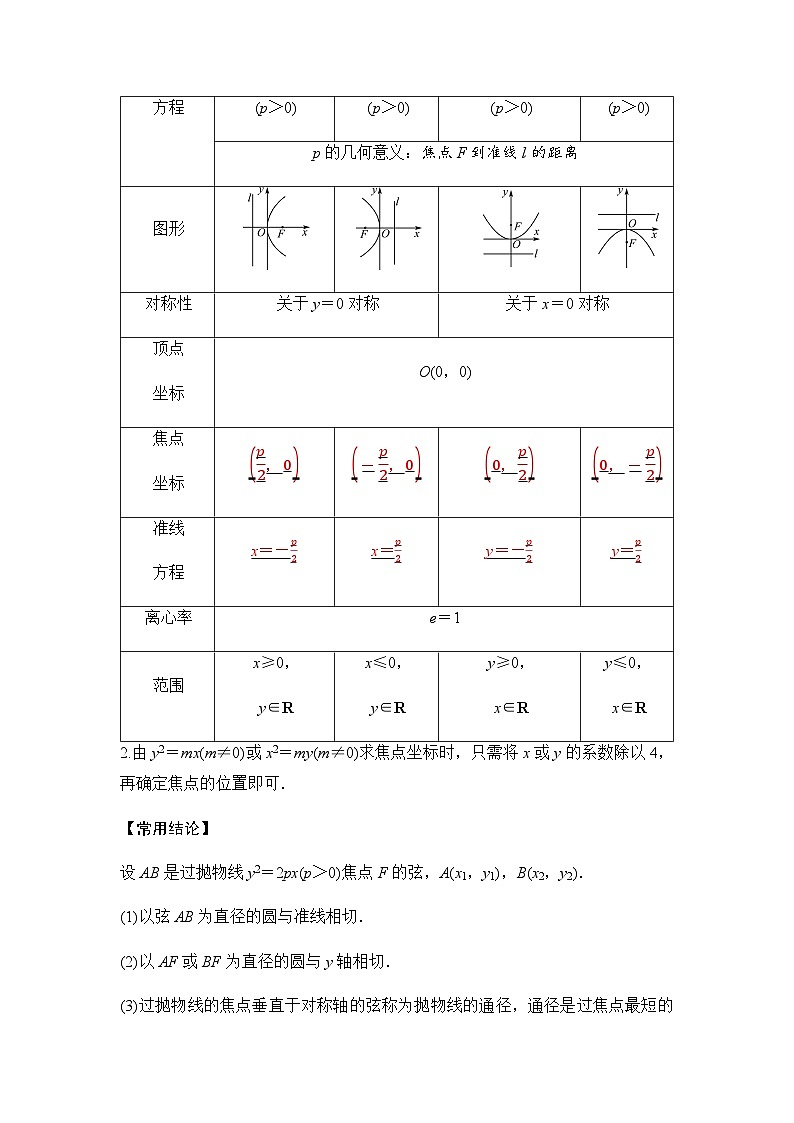
1．抛物线的标准方程和几何性质
2.由y2＝mx(m≠0)或x2＝my(m≠0)求焦点坐标时，只需将x或y的系数除以4，再确定焦点的位置即可．
【常用结论】
设AB是过抛物线y2＝2px(p＞0)焦点F的弦，A(x1，y1)，B(x2，y2)．
(1)以弦AB为直径的圆与准线相切．
(2)以AF或BF为直径的圆与y轴相切．
(3)过抛物线的焦点垂直于对称轴的弦称为抛物线的通径，通径是过焦点最短的弦，长为2p.
(4)AF＝x1＋p2，BF＝x2＋p2，AB＝x1＋x2＋p.
应用1 抛物线y2＝2px(p＞0)上一点M(3，m)到焦点F的距离|MF|＝4，则抛物线的方程为( )
A．y2＝8xB．y2＝4x
C．y2＝2xD．y2＝x
B 解析：由题意可得|MF|＝xM＋p2＝3＋p2＝4，解得p＝2，故抛物线的方程为y2＝4x.
应用2 过抛物线y2＝4x的焦点的直线l交抛物线于P(x1，y1)，Q(x2，y2)两点，如果x1＋x2＝6，则|PQ|等于( )
A．9B．8
C．7D．6
B 解析：根据题意可得2p＝4，即p＝2，所以|PQ|＝x1＋x2＋2＝8.
抛物线的标准方程
1．已知A为抛物线C：y2＝2px(p＞0)上一点，点A到C的焦点的距离为12，到y轴的距离为9，则p＝( )
A．2B．3
C．6D．9
C 解析：(方法一)因为点A到y轴的距离为9，
所以可设点A(9，yA)，
所以yA2＝18p.
又点A到焦点p2，0的距离为12，
所以9-p22+yA2＝12，
所以9-p22＋18p＝122，即p2＋36p－252＝0，
解得p＝6或p＝－42(舍去)．
(方法二)根据抛物线的定义及题意，得点A到抛物线C的准线x＝－p2的距离为12，又因为点A到y轴的距离为9，所以p2＝12－9，解得p＝6.
2．(多选题)设抛物线C：y2＝2px(p＞0)的焦点为F，点M在抛物线C上，|MF|＝5.若以|MF|为直径的圆过点(0，2)，则抛物线C的方程为( )
A．y2＝4xB．y2＝8x
C．y2＝16xD．y2＝2x
AC 解析：抛物线C：y2＝2px(p＞0)的焦点为Fp2，0，设M(x0，y0)，由题意及抛物线的定义，知|MF|＝x0＋p2＝5，得x0＝5－p2，则以MF为直径的圆的圆心横坐标为52，而圆的半径为52，所以该圆与y轴相切，切点为(0，2)，得圆心的纵坐标为2，则点M的纵坐标为4，即M5-p2，4，从而有42＝2p5-p2，整理得p2－10p＋16＝0，解得p＝2或p＝8，所以抛物线C的方程为y2＝4x或y2＝16x.
3．(2024·威海模拟)如图，过抛物线y2＝2px(p＞0)的焦点F的直线依次交抛物线及准线于点A，B，C．若|BC|＝2|BF|，且|AF|＝3，则抛物线的方程为( )
A．y2＝32xB．y2＝9x
C．y2＝92xD．y2＝3x
D 解析：如图，分别过点A，B作准线的垂线，交准线于点E，D.
设|BF|＝a，则|BC|＝2a.
由抛物线的定义得|BD|＝|BF|＝a，故易知∠BCD＝30°，
所以在Rt△ACE中，2|AE|＝|AC|.
因为|AE|＝|AF|＝3，|AC|＝3＋3a，
所以3＋3a＝6，解得a＝1.
因为BD∥FG，所以1p＝23，
所以p＝32，
因此抛物线的方程为y2＝3x.
求抛物线标准方程的方法
(1)定义法：若题目已给出抛物线的方程(含有未知数p)，那么只需求出p即可．
(2)待定系数法：若题目未给出抛物线的方程，对于焦点在x轴上的抛物线的标准方程可设为y2＝ax(a≠0)，焦点在y轴上的抛物线的标准方程可设为x2＝ay(a≠0)，a的正负由题设来定．这样就减少了不必要的讨论．
抛物线的定义及应用
【例1】(1)(2022·全国乙卷)设F为抛物线C：y2＝4x的焦点，点A在C上，点B(3，0)，若|AF|＝|BF|，则|AB|等于( )
A．2B．22
C．3D．32
B 解析：(方法一)由题意可知F(1，0)，抛物线的准线方程为x＝－1.
设Ay024，y0，则由抛物线的定义可知|AF|＝y024＋1.
因为|BF|＝3－1＝2，所以y024＋1＝2，解得y0＝±2，
所以A(1，2)或A(1，－2)．
则|AB|＝1-32+22＝8＝22.
(方法二)由题意可知F(1，0)，故|BF|＝2，
所以|AF|＝2.
因为抛物线的通径长为2p＝4，
故AF的长为通径长的一半，所以AF⊥x轴，
所以|AB|＝AF2+BF2＝22+22＝8＝22.
(2)若P是抛物线y2＝8x上的动点，点P到y轴的距离为d1，到圆C：(x＋3)2＋(y－3)2＝4上动点Q的距离为d2，则d1＋d2的最小值为 ．
34－4 解析：圆C：(x＋3)2＋(y－3)2＝4的圆心为C(－3，3)，半径r＝2，抛物线y2＝8x的焦点为F(2，0)．
由题意及抛物线定义可知d1＋d2＝|PF|－2＋d2＝|PF|＋|PQ|－2≥|PF|＋|PC|－|CQ|－2＝|PF|＋|PC|－4，所以要使d1＋d2最小，只需点P到抛物线的焦点与到圆C的圆心的距离之和最小．
如图，连接PF，FC，易知当点F，P，C共线时，|PF|＋|PC|取得最小值为|FC|，
则d1＋d2的最小值为|FC|－4＝-3-22+3-02－4＝34－4.
利用抛物线的定义可解决的常见问题
1．已知抛物线y＝mx2(m＞0)上的点(x0，2)到该抛物线焦点F的距离为114，则m等于( )
A．4B．3
C．14D．13
D 解析：由题意知，抛物线y＝mx2(m＞0)的准线方程为y＝－14m，
根据抛物线的定义，可得点(x0，2)到焦点F的距离等于到准线y＝－14m的距离，
即2＋14m＝114，解得m＝13．
2．已知点M(20，40)不在抛物线C：y2＝2px(p＞0)上，抛物线C的焦点为F.若对于抛物线上的一点P，|PM|＋|PF|的最小值为41，则p的值等于 ．
42或22 解析：当点M(20，40)位于抛物线内时，如图1，过点P作抛物线准线的垂线，垂足为D，
则|PF|＝|PD|，|PM|＋|PF|＝|PM|＋|PD|.
当点M，P，D共线时，
|PM|＋|PF|的值最小．
由最小值为41，得20＋p2＝41，解得p＝42，代入验证成立．
当点M(20，40)位于抛物线外时，
如图2，当点P，M，F三点共线时，
|PM|＋|PF|的值最小．
由最小值为41，得20-p22+402＝41，
解得p＝22或p＝58.
当p＝22时，代入验证成立；
当p＝58时，y2＝116x，
点M(20，40)在抛物线内，故舍去．
综上，p＝42或p＝22.
图1 图2
抛物线的性质
考向1 范围问题
【例2】(1)已知直线l1：4x－3y＋6＝0和直线l2：x＝－1，抛物线C：y2＝4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
A．355B．2
C．115D．3
B 解析：由题意可知l2：x＝－1 是抛物线的准线，设抛物线的焦点为F(1，0)，所以动点P到l2的距离等于|PF|，所以动点P到直线l1和直线l2的距离之和的最小值，即焦点F到直线l1：4x－3y＋6＝0的距离，如图所示．故最小值是4-0+65＝2.
(2)已知M是抛物线x2＝4y上一点，F为其焦点，点A在圆C：(x＋1)2＋(y－5)2＝1上，则|MA|＋|MF|的最小值是 ．
5 解析：依题意，由点M向抛物线x2＝4y的准线l：y＝－1引垂线，垂足为M1(图略)，则有|MA|＋|MF|＝|MA|＋|MM1|，结合图形可知|MA|＋|MM1|的最小值等于圆心C(－1，5)到直线y＝－1的距离再减去圆C的半径，即6－1＝5，因此|MA|＋|MF|的最小值是5.
与抛物线有关的最值问题的两个转化策略
(1)将抛物线上的点到准线的距离转化为该点到焦点的距离，构造出“两点之间，线段最短”，使问题得解．
(2)将抛物线上的点到焦点的距离转化为到准线的距离，利用“与直线上所有点的连线中，垂线段最短”原理解决．
考向2 弦长问题
【例3】(2024·济宁调研)过抛物线y2＝4x的焦点F的直线l与抛物线交于A，B两点，若|AF|＝2|BF|，则|AB|等于( )
A．4B．92
C．5D．6
B 解析：(方法一)易知直线l的斜率存在，设为k(k≠0)，则其方程为y＝k(x－1)．
由y=kx-1，y2=4x， 消去y，
得k2x2－(2k2＋4)x＋k2＝0，
得xA·xB＝1①.
因为|AF|＝2|BF|，由抛物线的定义得
xA＋1＝2(xB＋1)，即xA＝2xB＋1②，
由①②解得xA＝2，xB＝12，
所以|AB|＝xA＋xB＋p＝92．
(方法二)由对称性不妨设点A在x轴的上方，如图，设点A，B在准线上的射影分别为D，C，作BE⊥AD于点E.
设|BF|＝m，直线l的倾斜角为θ，则|AB|＝3m，
由抛物线的定义知|AD|＝|AF|＝2m，
|BC|＝|BF|＝m，
所以cs θ＝AEAB＝13，
所以sin2θ＝89．
由y2＝4x，知2p＝4，
故利用弦长公式得|AB|＝2psin2θ＝92．
(方法三)因为|AF|＝2|BF|，
所以1AF＋1BF＝12BF＋1BF＝32BF＝2p＝1，解得|BF|＝32，|AF|＝3，
故|AB|＝|AF|＋|BF|＝92．
[变式] 本例中抛物线方程不变，抛物线与直线2x＋y－4＝0交于A，B两点，则|FA|＋|FB|＝ ．
7 解析：设A(x1，y1)，B(x2，y2)，
联立(2x+y-4=0，y2=4x，
联立化简整理可得x2－5x＋4＝0，
由根与系数的关系，可得x1＋x2＝5.
因为抛物线y2＝4x，所以2p＝4，即p＝2，
根据抛物线的定义可得|FA|＋|FB|＝x1＋p2＋x2＋p2＝x1＋x2＋p＝5＋2＝7.
1．有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点．若过抛物线的焦点，可直接使用公式|AB|＝x1＋x2＋p；若不过焦点，则必须用一般弦长公式．
2．涉及抛物线的弦长、中点、距离等相关问题时，一般利用一元二次方程根与系数的关系采用“设而不求”“整体代入”等解法．
1．在抛物线y＝2x2上有一点P，它到点A(1，3)的距离与它到焦点的距离之和最小，则点P的坐标是( )
A．(－2，1)B．(1，2)
C．(2，1)D．(－1，2)
B 解析：如图所示，直线l为抛物线y＝2x2的准线，F为其焦点，PN⊥l，AN1⊥l.由抛物线的定义，知|PF|＝|PN|，所以|AP|＋|PF|＝|AP|＋|PN|≥|AN1|，当且仅当A，P，N三点共线时取等号，此时点P(1，2)．
2．如图，过抛物线y2＝2px(p＞0)的焦点F的直线交抛物线于点A，B，交其准线l于点C．若F是AC的中点，且|AF|＝4，则线段AB的长为( )
A．5B．6
C．163D．203
C 解析：如图．
设l与x轴交于点M，过点A作AD⊥l交l于点D，由抛物线的定义，知|AD|＝|AF|＝4，由F是AC的中点，知|AD|＝2|MF|＝2p，所以2p＝4，解得p＝2，所以抛物线的方程为y2＝4x.
(方法一)设A(x1，y1)，B(x2，y2)，则|AF|＝x1＋p2＝x1＋1＝4，所以x1＝3，可得y1＝23，所以A(3，23)．
又F(1，0)，所以直线AF的斜率k＝23-03-1＝3，
所以直线AF的方程为y＝3(x－1)，
代入抛物线方程y2＝4x，得3x2－10x＋3＝0，
所以x1＋x2＝103，|AB|＝x1＋x2＋p＝163．
(方法二)设A(x1，y1)，B(x2，y2)，
则|AF|＝x1＋p2＝x1＋1＝4，
所以x1＝3.
又x1x2＝p24＝1，所以x2＝13，
所以|AB|＝x1＋x2＋p＝3＋13＋2＝163．
(方法三)因为1AF＋1BF＝2p，|AF|＝4，p＝2，
所以|BF|＝43，
所以|AB|＝|AF|＋|BF|＝4＋43＝163．
课时质量评价(五十二)
1．动圆与定圆A：(x＋2)2＋y2＝1外切，且和直线x＝1相切，则动圆圆心的轨迹是( )
A．直线B．椭圆
C．双曲线D．抛物线
D 解析：设动圆的圆心为C，半径为r，则C到定圆A：(x＋2)2＋y2＝1的圆心的距离等于r＋1，而C到直线x＝1的距离等于r，所以C到直线x＝2的距离为r＋1，根据抛物线的定义知，动圆圆心的轨迹为抛物线．
2．(2021·新高考全国Ⅱ卷)抛物线y2＝2px(p＞0)的焦点到直线y＝x＋1的距离为2，则p＝( )
A．1B．2
C．22D．4
B 解析：抛物线的焦点坐标为p2，0，其到直线x－y＋1＝0的距离为d＝p2-0+11+1＝2，解得p＝2(p＝－6舍去)．
3．(2024·榆林模拟)已知抛物线x2＝2py(p＞0)上的一点M(x0，1)到其焦点的距离为2，则该抛物线的焦点到其准线的距离为( )
A．6B．4
C．3D．2
D 解析：由题可知，抛物线的准线为y＝－p2，可得1＋p2＝2，解得p＝2，所以该抛物线的焦点到其准线的距离为p＝2.
4．设抛物线C：y2＝2px(p＞0)的焦点为F，准线为l，M(5，y0)为抛物线C上一点，以M为圆心的圆M与准线l相切，且过点E(9，0)，则抛物线的方程为( )
A．y2＝4x
B．y2＝2x
C．y2＝36x
D．y2＝4x或y2＝36x
D 解析：由抛物线的定义知，圆M经过焦点Fp2，0，点M的横坐标为5，由题意，当E，F不重合时，M是线段EF垂直平分线上的点，所以5＝p2+92，所以p＝2，所以抛物线C的方程为y2＝4x；当E，F重合时，p2＝9，所以p＝18，所以抛物线C的方程为y2＝36x.
5．(多选题)(2023·新高考全国Ⅱ卷)设O为坐标原点，直线y＝－3(x－1)过抛物线C：y2＝2px(p＞0)的焦点，且与C交于M，N两点，l为C的准线，则( )
A．p＝2
B．|MN|＝83
C．以MN为直径的圆与l相切
D．△OMN为等腰三角形
AC 解析：直线y＝－3(x－1)过抛物线C：y2＝2px(p＞0)的焦点，可得p2＝1，所以p＝2，所以A正确；
抛物线方程为y2＝4x，联立直线方程可得3x2－10x＋3＝0，xM＋xN＝103，所以|MN|＝xM＋xN＋p＝163，所以B不正确；
M，N的中点的横坐标为53，中点到抛物线的准线l的距离为1＋53＝83＝12|MN|，所以以MN为直径的圆与l相切，所以C正确；
因为3x2－10x＋3＝0，所以不妨取xM＝3，xN＝13，则yM＝－23，yN＝233，
|OM|＝9+12＝21，|ON|＝19+129＝133，|MN|＝163，
所以△OMN不是等腰三角形，所以D不正确．
6．已知A(2，0)，B为抛物线y2＝x上一点，则|AB|的最小值为 ．
72 解析：设B(x，y)，则x＝y2≥0，
所以|AB|＝x-22+y2＝x-22+x
＝x2-3x+4＝x-322+74 .
所以当x＝32时，|AB|取得最小值，且|AB|min＝72．
7．已知抛物线C：y2＝4x，焦点为F，点M为抛物线C上的一点，且|FM|＝6，则M的横坐标是 ，作MN⊥x轴于点N，则S△FMN＝ ．
5 45 解析：因为抛物线的方程为y2＝4x，故p＝2且F(1，0)．
因为|FM|＝6，所以xM＋p2＝6，解得xM＝5，
故yM＝±25，
所以S△FMN＝12×(5－1)×25＝45.
8．如图所示，抛物线关于x轴对称，它的顶点在坐标原点，点P(1，2)，A(x1，y1)，B(x2，y2)均在抛物线上．
(1)写出该抛物线的方程及其准线方程；
(2)当PA与PB的斜率存在且倾斜角互补时，求y1＋y2的值及直线AB的斜率．
解：(1)由已知条件，可设抛物线的方程为
y2＝2px(p＞0)．
因为点P(1，2)在抛物线上，
所以22＝2p×1，解得p＝2.
故所求抛物线的方程是y2＝4x，
准线方程是x＝－1.
(2)由题意可知kPA＝y1-2x1-1(x1≠1)，kPB＝y2-2x2-1(x2≠1)，
因为PA与PB的斜率存在且倾斜角互补，
所以kPA＝－kPB.
由A(x1，y1)，B(x2，y2)均在抛物线上，
得y12=4x1①，y22=4x2②，所以y1-214y12-1＝－y2-214y22-1，
整理得y1＋2＝－(y2＋2)，所以y1＋y2＝－4.
由①－②，得y12-y22＝4(x1－x2)，
所以kAB＝y1-y2x1-x2＝4y1+y2＝－1(x1≠x2)．
9．已知抛物线y2＝2px的焦点F与双曲线x27－y29＝1的右焦点重合，抛物线的准线与x轴的交点为K，点A在抛物线上，且|AK|＝2|AF|，则△AFK的面积为( )
A．4B．8
C．16D．32
D 解析：由题可知抛物线的焦点坐标为(4，0)，所以p＝8.过点A作直线AA′垂直于抛物线的准线，垂足为A′(图略)，根据抛物线定义知，|AA′|＝|AF|.在△AA′K中，|AK|＝2|AA′|，故∠KAA′＝45°，所以直线AK的倾斜角为45°，直线AK的方程为y＝x＋4，代入抛物线方程y2＝16x得y2＝16(y－4)，即y2－16y＋64＝0，解得y＝8，x＝4，即A(4，8)，所以△AFK为直角三角形，故△AFK的面积为12×8×8＝32.
10．(多选题)已知F是抛物线C：y2＝16x的焦点，M是C上一点，FM的延长线交y轴于点N.若M为FN的中点，则( )
A．C的准线方程为x＝－4
B．点F的坐标为(0，4)
C．|FN|＝12
D．△ONF的面积为162(O为坐标原点)
ACD 解析：如图，不妨设点M位于第一象限，设抛物线的准线l与x轴交于点F′，作MB⊥l于点B，NA⊥l于点A．由抛物线的解析式可得准线方程为x＝－4，点F的坐标为(4，0)，则|AN|＝4，|FF′|＝8.在直角梯形ANFF′中，中位线|MB|＝AN+FF'2＝6.由抛物线的定义知|MF|＝|MB|＝6，结合题意，有|MN|＝|MF|＝6，故|FN|＝|MF|＋|MN|＝6＋6＝12，|ON|＝122-42＝82，S△ONF＝12×82×4＝162.
11．已知F1，F2分别是双曲线3x2－y2＝3a2(a＞0)的左、右焦点，P是抛物线y2＝8ax与双曲线的一个交点．若|PF1|＋|PF2|＝12，则抛物线的准线方程为 ．
x＝－2 解析：将双曲线方程化为标准方程得x2a2－y23a2＝1，则F1(－2a，0)，F2(2a，0)．
抛物线的准线为x＝－2a，联立x2a2-y23a2=1，y2=8ax，解得x＝3ax=-a3舍去，
即点P的横坐标为3a.
而由PF1+PF2=12，PF1-PF2=2a，得|PF2|＝6－a，
所以|PF2|＝3a＋2a＝6－a，得a＝1，
所以抛物线的准线方程为x＝－2.
12．已知抛物线C：y2＝2px(p＞0)的焦点为F，准线为l，M是抛物线C上一点，MH⊥l于点H.若|MH|＝4，∠HFM＝60°，则抛物线C的方程为 ．
y2＝4x 解析：如图，因为抛物线上的点到焦点的距离等于到准线的距离，
所以|MF|＝|MH|＝4.又∠HFM＝60°，
所以△MHF为正三角形，所以|HF|＝4.
记准线l与x轴交于点Q，则∠QHF＝30°，
所以p＝|QF|＝|HF|sin ∠QHF＝4sin 30°＝2，
所以该抛物线的方程为y2＝4x.
13．已知在抛物线C：x2＝2py(p＞0)的第一象限的点P(x，1)到其焦点的距离为2.
(1)求抛物线C的方程和点P的坐标；
(2)过点-1，12的直线l交抛物线C于A，B两点，若∠APB的角平分线与y轴垂直，求弦AB的长．
解：(1)由1＋p2＝2，可得p＝2，
故抛物线C的方程为x2＝4y.
当y＝1时，x2＝4，又点P(x，1)在第一象限，所以x＝2，
所以点P的坐标为(2，1)．
(2)由题意可知直线l的斜率存在，
设直线l的方程为y＝k(x＋1)＋12，A(x1，y1)，B(x2，y2)，
联立y=kx+k+12，x2=4y， 得x2－4kx－4k－2＝0，
所以Δ＝16k2＋4(4k＋2)＞0，
x1＋x2＝4k，x1x2＝－4k－2.
因为∠APB的角平分线与y轴垂直，
所以kPA＋kPB＝0，
即y1-1x1-2＋y2-1x2-2＝0，
即x124-1x1-2＋x224-1x2-2＝0，整理得x1＋x2＋4＝0，
所以x1＋x2＝－4，即k＝－1，x1x2＝2，
所以|AB|＝1+k2|x1－x2|＝1+k2·x1+x22-4x1x2＝4.
14．(2024·郑州模拟)已知抛物线C：x2＝2py(p＞0)的焦点为F，直线x＝4与x轴的交点为M，与抛物线C的交点为N，且|NF|＝54|MN|.
(1)求抛物线C的方程；
(2)设过定点(0，6)的直线l与抛物线C交于P，Q两点，连接QF并延长交抛物线的准线于点R，当直线PR恰与抛物线相切时，求直线l的方程．
解：(1)设N(4，y1)，代入x2＝2py，得y1＝8p，
所以|MN|＝8p，|NF|＝p2＋y1＝p2＋8p．
由题设得p2＋8p＝54×8p，
解得p＝2或p＝－2(舍去)，
所以抛物线C的方程为x2＝4y.
(2)由题知直线l的斜率存在，设其方程为y＝kx＋6，
由y=kx+6，x2=4y， 消去y，整理得x2－4kx－24＝0，
显然Δ＝16k2＋96＞0.
如图，设P(x1，y1)，Q(x2，y2)，则x1+x2=4k，x1x2=-24，
抛物线C在点Px1，x124处的切线方程为y－x124＝x12(x－x1)，
令y＝－1，得x＝x12-42x1，可得Rx12-42x1，-1．
由Q，F，R三点共线得kQF＝kFR，
所以x224-1x2＝-1-1x12-42x1，
即(x12-4)(x22－4)＋16x1x2＝0，
整理得(x1x2)2－4[(x1＋x2)2－2x1x2]＋16＋16x1x2＝0，
所以(－24)2－4[(4k)2－2×(－24)]＋16＋16×(－24)＝0，
解得k2＝14，即k＝±12，
故所求直线l的方程为y＝12x＋6或y＝－12x＋6.
标准
方程
y2＝2px
(p＞0)
y2＝－2px
(p＞0)
x2＝2py
(p＞0)
x2＝－2py
(p＞0)
p的几何意义：焦点F到准线l的距离
图形
对称性
关于y＝0对称
关于x＝0对称
顶点
坐标
O(0，0)
焦点
坐标
p2，0
-p2，0
0，p2
0，-p2
准线
方程
x＝－p2
x＝p2
y＝－p2
y＝p2
离心率
e＝1
范围
x≥0，
y∈R
x≤0，
y∈R
y≥0，
x∈R
y≤0，
x∈R
轨迹
问题
用抛物线的定义可以确定与定点、定直线距离有关的动点轨迹是否为抛物线
距离
问题
灵活地进行抛物线上的点到焦点距离与其到准线距离间的等价转化．“看到准线应该想到焦点，看到焦点应该想到准线”，这是解决抛物线中与距离有关问题的有效途径