





人教A版普通高中数学一轮复习第2章第4节二次函数与幂函数课件
展开必备知识 落实“四基”
3.如图是①y=xa;②y=xb;③y=xc在第一象限的图象,则a,b,c的大小关系为( )A.c
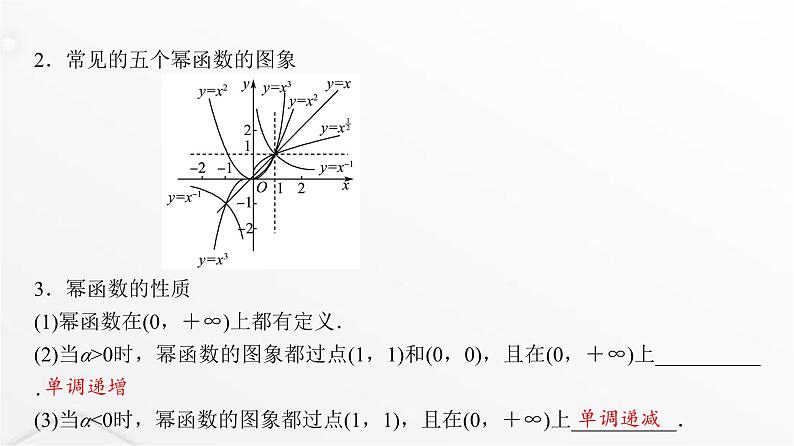
2.常见的五个幂函数的图象3.幂函数的性质(1)幂函数在(0,+∞)上都有定义.(2)当α>0时,幂函数的图象都过点(1,1)和(0,0),且在(0,+∞)上__________.(3)当α<0时,幂函数的图象都过点(1,1),且在(0,+∞)上__________.
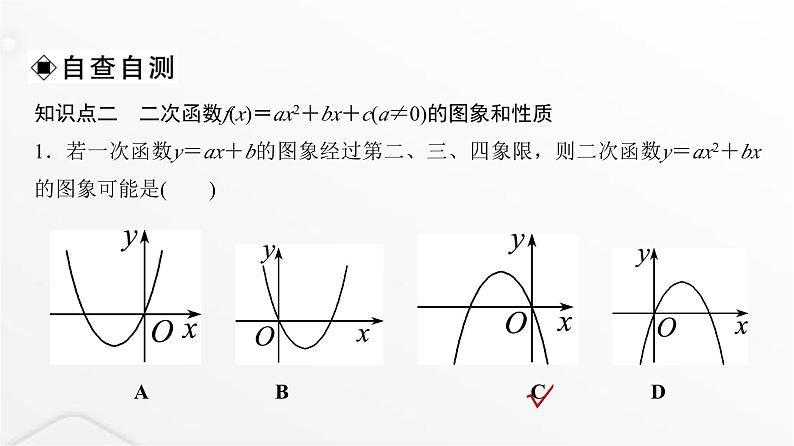
知识点二 二次函数f(x)=ax2+bx+c(a≠0)的图象和性质1.若一次函数y=ax+b的图象经过第二、三、四象限,则二次函数y=ax2+bx的图象可能是( )
A B C D
2.函数y=-x2+6x(0≤x≤5)的值域是( )A .[0,5]B.[0,9]C .[5,9]D.[0,+∞) B 解析:函数y=-x2+6x的图象是一条开口向下的抛物线,对称轴为直线x=3,所以该函数在[0,3)上单调递增,在(3,5]上单调递减,所以ymax=y|x=3=9.又y|x=0=0,y|x=5=5,所以ymin=0,即函数的值域为[0,9].故选B.
二次函数f(x)=ax2+bx+c(a≠0)的图象和性质
应用 幂函数f(x)=xa2-10a+23(a∈Z)为偶函数,且f(x)在区间(0,+∞)上单调递减,则a=( )A.3B.4C.5D.6C 解析:因为a2-10a+23=(a-5)2-2,f(x)=x(a-5)2-2(a∈Z)为偶函数,且在区间(0,+∞)上单调递减,所以(a-5)2-2<0,从而a=4,5,6.又(a-5)2-2为偶数,所以a=5.故选C.
核心考点 提升“四能”
反思感悟幂函数图象与性质的应用(1)可以借助幂函数的图象理解函数的对称性、单调性.(2)在比较幂值的大小时,必须结合幂值的特点,选择适当的函数,借助其单调性进行比较,准确掌握各个幂函数的图象和性质是解题的关键.
反思感悟求二次函数解析式的方法
2.已知二次函数f(x)的图象经过点(4,3),在x轴上截得的线段长为2,并且对任意x∈R,都有f(2-x)=f(2+x),求函数f(x)的解析式.解:因为f(2-x)=f(2+x)对任意x∈R恒成立,所以f(x)图象的对称轴为直线x=2.因为f(x)的图象被x轴截得的线段长为2,所以f(x)=0的两根为1和3.设f(x)=a(x-1)(x-3)(a≠0).因为f(x)的图象经过点(4,3),所以a(4-1)(4-3)=3,解得a=1.所以f(x)=(x-1)(x-3),即f(x)=x2-4x+3.
二次函数的图象和性质考向1 二次函数的图象及应用【例2】(多选题)(2024·临沂模拟)二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )A.b=-2a B.a+b+c<0C.a-b+c>0 D.abc<0
反思感悟识别二次函数图象应学会“三看”
(2)设二次函数f(x)=ax2-2ax+c在区间[0,1]上单调递减,且f(m)≤f(0),则实数m的取值范围是__________.[0,2] 解析:依题意a≠0,二次函数f(x)=ax2-2ax+c图象的对称轴是直线x=1.因为函数f(x)在区间[0,1]上单调递减,所以a>0,即函数图象的开口向上,所以f(0)=f(2),则当f(m)≤f(0)时,有0≤m≤2,故实数m的取值范围为[0,2].
反思感悟二次函数的最值与单调性(1)二次函数在闭区间上的最值主要有三种类型:轴定区间定、轴动区间定、轴定区间动.不论哪种类型,解题的关键都是对称轴与区间的位置关系,当含有参数时,要依据对称轴与区间的位置关系进行分类讨论.(2)二次函数的单调性问题主要依据二次函数图象的对称轴进行分类讨论求解.
考向3 与二次函数有关的恒成立问题【例4】已知函数f(x)=x2+2x+1,f(x)>x+k在区间[-3,-1]上恒成立,则k的取值范围为__________(-∞,1) 解析:由题意得x2+x+1>k在区间[-3,-1]上恒成立.设g(x)=x2+x+1,x∈[-3,-1],易知g(x)在[-3,-1]上单调递减,所以g(x)min=g(-1)=1,所以k<1.故k的取值范围为(-∞,1)..
反思感悟由不等式恒成立求参数取值范围的思路(1)一般有两种解题思路:一是分离参数;二是不分离参数.(2)两种思路都是将问题归结为求函数的最值,这两个思路的依据是:a≥f(x)恒成立⇔a≥f(x)max,a≤f(x)恒成立⇔a≤f(x)min.
1.(多选题)设函数f(x)=x2+x+a(a>0).若f(m)<0,则下列不等式正确的是( )A.f(m+1)>0 B.f(m+1)<0C.f(-2-m)>0 D.f(-2-m)<0
人教A版普通高中数学一轮复习第3章第2节微专题隐零点问题课件: 这是一份人教A版普通高中数学一轮复习第3章第2节微专题隐零点问题课件,共6页。
人教A版普通高中数学一轮复习第3章微专题公切线问题课件: 这是一份人教A版普通高中数学一轮复习第3章微专题公切线问题课件,共6页。PPT课件主要包含了思维建模等内容,欢迎下载使用。
人教A版普通高中数学一轮复习第2章第3节微专题抽象函数的性质课件: 这是一份人教A版普通高中数学一轮复习第2章第3节微专题抽象函数的性质课件,共12页。PPT课件主要包含了思维建模等内容,欢迎下载使用。













