福建省龙岩市上杭县东南片区2023-2024学年七年级下学期期中考试数学试卷(含解析)

这是一份福建省龙岩市上杭县东南片区2023-2024学年七年级下学期期中考试数学试卷(含解析)，共15页。试卷主要包含了选择题等内容，欢迎下载使用。
上杭县2023-2024学年第二学期片区半期联考
七年级数学试题
（考试时间：120分钟，满分：150分）
一、选择题（本题共10个小题，每小题4分，共40分）
1．下列各数中，是无理数的是（ ）
A．B．C．D．
2．在平面直角坐标系中，下列各点在第四象限的是（ ）
A．B．C．D．
3．下列车标中哪一个可以看成是由图案自身一部分经平移后得到的？（ ）
A． B． C． D．
4．7的算术平方根是（ ）
A．B．C．D．
5．如图，直线被直线所截，，则的度数为（ ）
A．B．C．D．
6．下列命题中，属于假命题的是（ ）
A．三角形三个内角的和等于180°B．两直线平行，同位角相等
C．对顶角相等D．如果，则
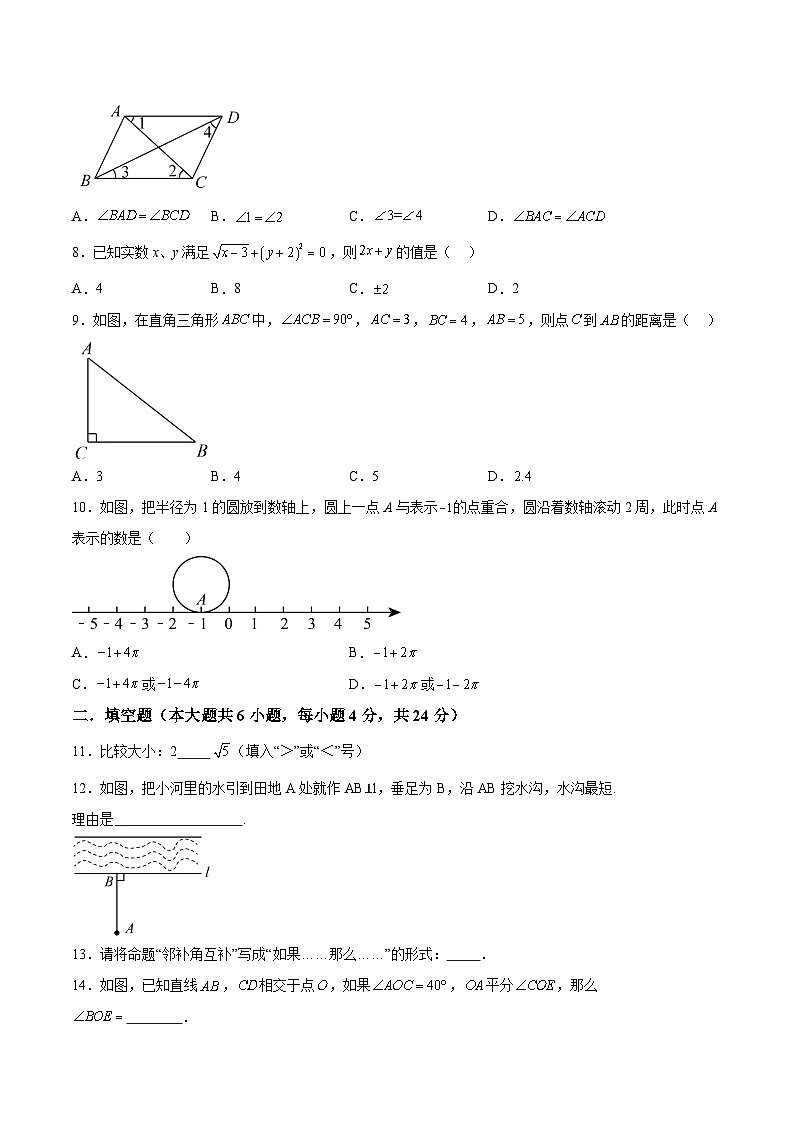
7．如图所示，下列条件中，能判断的是（ ）

A． B．C．D．
8．已知实数x、y满足，则的值是（ ）
A．4B．8C．D．2
9．如图，在直角三角形中，，，，，则点到的距离是（ ）

A．3B．4C．5D．
10．如图，把半径为1的圆放到数轴上，圆上一点A与表示的点重合，圆沿着数轴滚动2周，此时点A表示的数是（ ）

A．B．
C．或D．或
二．填空题（本大题共6小题，每小题4分，共24分）
11．比较大小：2 （填入“＞”或“＜”号）
12．如图，把小河里的水引到田地A处就作AB⊥l，垂足为B，沿AB挖水沟，水沟最短.
理由是 .
13．请将命题“邻补角互补”写成“如果……那么……”的形式： ．
14．如图，已知直线，相交于点，如果，平分，那么 ．

15．如图，直角三角形沿方向平移得到三角形，，，平移距离为6，则图中阴影部分面积为 ．
16．如图，在平面直角坐标系中，有若干个坐标分别为整数的点，其顺序按图中“”方向排列，如，，，，，，……．根据这个规律，第2024个点的坐标为 ．
三．解答题（本大题共9小题，满分86分）
17．计算：
(1)
(2)
18．解方程：
(1)；
(2) ．
19．如图，直线CD与直线AB相交于C，根据下列语句画图、解答．
（1）过点P作PQCD，交AB于点Q；
（2）过点P作PR⊥CD，垂足为R；
（3）若∠DCB=120°，猜想∠PQC是多少度？并说明理由
20．补全下面的推理．
如图，已知，，求．
解∶∵
∴ ( ____________________)；
又∵( ____________________)；
∴ ( ____________________)；
∴____( ____________________)；
∴______ ( ____________________)；
∵
∴________．
21．如图，在边长为1的正方形网格中，平移变换后的对应点的坐标为，、的对应点分别为、．
(1)请在图中画出，并直接写出、的坐标，______，_________；
(2)三角形的面积为________；
22．已知的立方根是3，的算术平方根是4，c是的整数部分．
(1)求a，b，c的值；
(2)求的平方根．
23．如图，在四边形中，，连接，点E在边上，点F在边上，且．

(1)求证：；
(2)若平分，，，求的度数．
24．在平面直角坐标系xOy中，对于点P（x，y），若点Q的坐标为（ax+y，x+ay），其中a为常数，则称点Q是点P的“a级关联点”例如，点P（1，4）的“3级关联点”为Q（3×1+4，1+3×4），即Q（7，13）．
(1)已知点A（2，-6）的“级关联点”是点B，求点B的坐标．
(2)已知点M（m﹣1，2m）的“﹣4级关联点”N位于坐标轴上．求点N的坐标．
25．（1）【问题】
如图1，若，，．求的度数；
（2）【问题迁移】
如图2，，点P在AB的上方，问，，之间有何数量关系？请说明理由；
（3）【联想拓展】
如图3所示，在（2）的条件下，已知，的平分线和的平分线交于点G，用含有α的式子表示∠G的度数．
参考答案与解析
1．A
解析：解：为无理数，，，是有理数．
故选：A．
2．C
解析：解：A：点在第一象限，故A错误；
B：点在第二象限，故B错误；
C：点在第四象限，故C正确；
D：点在第三象限，故D错误
故选：C．
3．D
解析：
解：“ ”可以看成是由图案自身一部分经平移后得到的，
故选：D．
4．C
解析：7的算术平方根是．
故选：C．
5．B
解析：解：如图，
∵，
∴，
∵，
∴，
∴．
故选：B．
6．D
解析：解：三角形三个内角的和等于，故A是真命题，不符合题意；
两直线平行，同位角相等，故B是真命题，不符合题意；
对顶角相等，故C是真命题，不符合题意；
如果，则a=±b，故D是假命题，符合题意；
故选：D．
7．D
解析：解：A、根据，不能判断，故该选项错误；
B、根据，能判断，故该选项错误；
C、根据，能判断，故该选项错误；
D、根据，能判断，故该选项正确；
故选：D．
8．A
解析：解：∵，，
又∵，
∴，，
则，，
∴．
故选：A．
9．D
解析：解：∵在直角三角形中，，
∴，
∵，，，
∴，
∴，
故选：D．
10．C
解析：解：∵，
∴圆沿着数轴滚动2周后点A与起始位置距离为：，
∵点A起始位置表示，
∴当圆向右滚动2周后点A表示的数为，当圆向左滚动2周后点A表示的数为，
故选：C．
11．
解析：解：∵4＜5，
∴2＜．
故答案为：．
12．垂线段最短
解析：试题分析：点到直线的所有线段中垂线段最短.
考点：垂线段的性质
13．如果两个角是邻补角，那么这两个角互补
解析：命题“邻补角互补”写成“如果……那么……”的形式为：如果两个角是邻补角，那么这两个角互补．
故答案为：如果两个角是邻补角，那么这两个角互补．
14．##140度
解析：解：∵，平分，
∴，
∴，
故答案为：．
15．39
解析：解：由平移的性质可得，，，，
∴，，
∴，
故答案为：39．
16．
解析：解：由图可知：第一个正方形每条边上有2个点，共有个点，且终点为；
第二个正方形每条边上有3个点，连同第一个正方形共有个点，且终点为；
第三个正方形每条边上有4个点，连同前两个正方形共有个点，且终点为；
第四个正方形每条边上有5个点，连同前两个正方形共有个点，且终点为；
故当n为奇数时，第n个正方形每条边上有个点，连同前边所有正方形共有个点，且终点为；当n为偶数时，第n个正方形每条边上有个点，连同前边所以正方形共有点，且终点为．
而，
，
解得：．
由规律可知，第44个正方形每条边上有个点，且终点坐标为，由图可知，再倒着推1个点的坐标为：．
故答案为：．
17．(1)
(2)
解析：（1）解：原式．
（2）解：原式．
18．(1)
(2)
解析：（1）解：，
方程两边同除以得：，
开平方得：；
（2）解：，
移项，合并同类项得：，
开立方得：．
19．（1）见解析；（2）见解析；（3）∠PQC=60°，理由见解析
解析：解：如图所示：
（1）画出如图直线PQ
（2）画出如图直线PR
（3）∠PQC=60°
理由是：因为PQCD
所以∠DCB+∠PQC=180°
又因为∠DCB=120°
所以∠PQC=180°－120°=60°
20．两直线平行，同位角相等；已知；等量代换；；内错角相等，两直线平行；；两直线平行，同旁内角互补；
解析：解：∵，
∴（两直线平行，同位角相等），
∵（已知），
∴（等量代换），
∴（内错角相等，两直线平行），
∴（两直线平行，同旁内角互补），
∵，
∴．
故答案为：两直线平行，同位角相等；已知；等量代换；；内错角相等，两直线平行；；两直线平行，同旁内角互补；．
21．(1)见解析；；
(2)7
解析：（1）解：即为所求的三角形．
；
（2）解：三角形的面积为：
．
22．(1)，，
(2)
解析：（1）∵的立方根是3，的算术平方根是4，是的整数部分
∴，，，
∴，，．
（2）∵，，，
∴，
∴．
23．(1)见解析
(2)
解析：（1）证明：如图，

∵，
∴
∵．
∴
∴
（2）解：∵，
∴
∵，
∴
∵平分，
∴
∴．
∵在中，
∵，
∴．
24．(1)
(2)N(0，-15) 或 N(，0)
解析：（1）因为点A（2，-6）的“级关联点”是点B，
所以点B的横坐标为，纵坐标为 ．
∴点B的坐标为（-5，-1）；
（2）∵点M（m-1，2m）的“-4级关联点”为N（-4（m-1）+2m，m-1+（-4）×2m），
当点N位于位于y轴上，
∴-4（m-1）+2m=0，
解得：m=2
∴m-1+（-4）×2m=-15，
∴N（0，-15）．
当点N位于位于x轴上，
m-1+（-4）×2m=0
解得，
∴-4（m-1）+2m=
∴N(，0)
综上，点N的坐标为：N(0，-15) 或 N(，0)
25．（1）；（2），见解析；（3）
解析：解：（1）如图1，过点P作，
，，
CD∥PQ．
，
又，
，
；
（2），
理由：如图2，过P点作，则，
，
，
，
，
，
；
（3）如图3，过点G作的平行线．
，，
，
，∠HGF=∠CFG，
又的平分线和的平分线交于点G，
，，
由（2）得，，
．