北师大版七年级上册1.2 展开与折叠课文课件ppt

这是一份北师大版七年级上册1.2 展开与折叠课文课件ppt，共26页。PPT课件主要包含了A级基础训练，B级能力训练，C级拓展训练等内容，欢迎下载使用。
数学 九年级上册 BS版
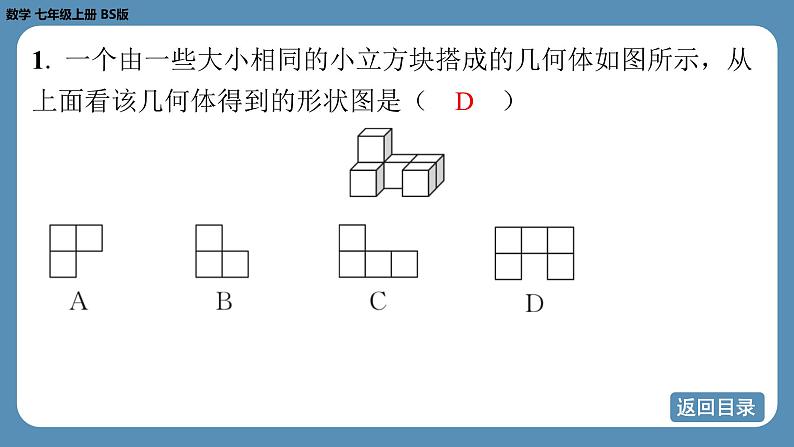
1. 一个由一些大小相同的小立方块搭成的几何体如图所示，从 上面看该几何体得到的形状图是（　D　）
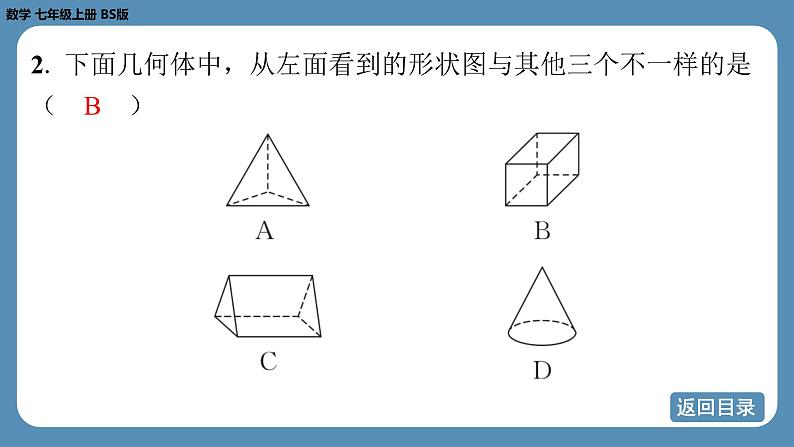
2. 下面几何体中，从左面看到的形状图与其他三个不一样的是 （　B　）
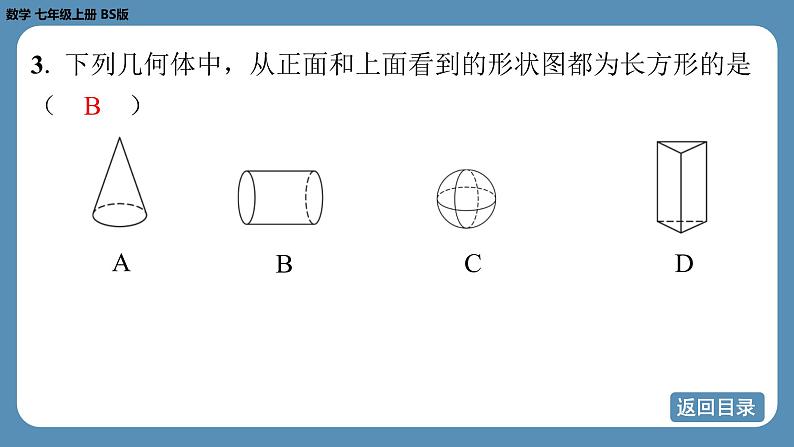
3. 下列几何体中，从正面和上面看到的形状图都为长方形的是 （　B　）
　　 　C　　　　　 D
4. 从正面、上面、左面观察一个球时，看到的形状图都 是 ；如果一个几何体从正面、上面、左面看时，看到的 形状图都是圆，则这个几何体可能是 ⁠.
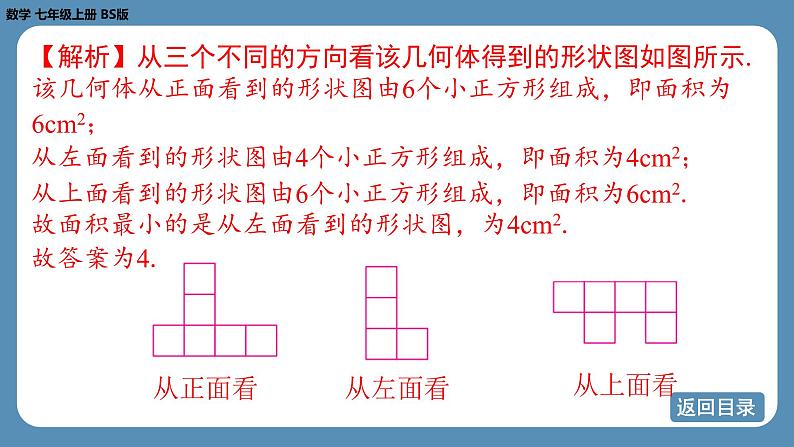
5. 一个由若干个棱长为1cm的小立方块搭成的几何体如图所示. 从正面、左面、上面观察该几何体，看到的形状图中，面积最 小为 cm2.
【解析】从三个不同的方向看该几何体得到的形状图如图所示.
该几何体从正面看到的形状图由6个小正方形组成，即面积为 6cm2；
从左面看到的形状图由4个小正方形组成，即面积为4cm2；
从上面看到的形状图由6个小正方形组成，即面积为6cm2.
故面积最小的是从左面看到的形状图，为4cm2.
6. 如图是由几个大小相同的小立方块搭成的几何体从不同方向 看到的形状图，则搭成这个几何体的小立方块有 个.
【解析】由三种形状图可得，需要的小立方块的个数为2＋1＋1＝4（个）.故答案为4.
解：观察三种形状图可知，该几何体为长方体，且该长方体的长、宽、高分别为12cm， 10cm和15cm.根据长方体的体积和表面积公式可知， V ＝12×10×15＝1 800（cm3）， S ＝（12×10＋12×15＋10×15）×2＝（120＋180＋150）×2＝450×2＝900（cm2）.故这个几何体的体积是1 800cm3，表面积是900cm2.
7. 一个几何体从正面、左面、上面看到的形状如图所示（单 位：cm），根据图中数据计算这个几何体的体积和表面积.
8. 把6个棱长均为1cm的小立方块按如图所示方式摆放.
（1）在下面的方格纸中画出从正面、左面、上面看到的该几何 体的形状图；
（2）若在该几何体上再添加一些相同的小立方块，并保持从左 面和上面看该几何体得到的形状图不变，则最多可以再添 加 个小立方块；
（3）求该几何体的体积.
（2）【解析】如果要保持从左面和上面看该几何体得到的形状 图不变，那么最多可以再在后面一行第一、二列各添加1个小立 方块.故答案为2.
（3）解：该几何体的体积为1×1×1×6＝6（cm3）.
9. 用小立方块搭建一个几何体，从正面和上面看该几何体得到 的形状图如图所示.设搭这样的几何体至少需要 n 个小立方块， 最多需要 m 个小立方块，则 m － n ＝ ⁠.
【解析】如图，搭成这样的几何体至少需要3＋2＋2＋1＋1＋1 ＋1＝11（个）小立方块，
最多需要3×3＋2×4＝17（个）小立方块，
故 m ＝17， n ＝11.
所以 m － n ＝17－11＝6.
10. 已知一个由若干个小立方块搭建而成的几何体，从正面和 左面看到的形状图如图所示，则下列图形中，可以作为该几何 体从上面看到的形状图的有 （填序号）.
【解析】如图，由题意可知，从上面看，
第二行第一列有3个小立方块，
第二行第二列有2个小立方块，
第一行有1个或2个小立方块.
11. 已知一个由一些棱长为2cm的小立方块所搭成的几何体，从 上面看到的形状图如图所示，小正方形中的数字表示该位置上 重叠的小立方块的个数.
（1）请分别画出从正面和从左面看到的形状图；
解：（1）从正面和左面看到的该几何体的形状图如图所示.
（2）求这个几何体的体积.
解： （2）由从上面看到的形状图可知，这个几何体由10个小立方块组成.因为小立方块的棱长为2cm，所以这个几何体的体积为23×10＝80（cm3）.
12. 如图所示的几何体是由16个棱长为1cm的小正方体堆积而成 的，问这个几何体的表面积是多少平方厘米？
解：从上面和下面看到的面积为2×9×（1×1）＝18（cm2），从正面和后面看到的面积为2×7×（1×1）＝14（cm2），从两个侧面看到的面积为2×9×（1×1）＝18（cm2）.故这个几何体的表面积是18＋14＋18＝50（cm2）.
13. （选做）已知用一些大小相同的小立方块搭一个几何体， 使该几何体从正面和从上面看到的形状图如图所示，从上面看 到的形状图中小正方形中的字母表示在该位置上的小立方块的 个数.解答下列问题：（1）求 d ， e ， f 的值；
解：（1）由从正面看到的形状图可知，从左到右第二列小立方 块的个数均为1，第三列小立方块的个数为3，所以 d ＝1， e ＝ 1， f ＝3.
（2）这个几何体最多由几个小立方块搭成？最少由几个小立方 块搭成？
解：（2）由从正面看到的形状图可知，从左到右第一列小立方块的个数最多为2＋2＋2＝6，最少为2＋1＋1＝4，所以这个几何体最多由6＋2＋3＝11（个）小立方块搭成；最少由4＋2＋3＝9 （个）小立方块搭成.
（3）当 a ＝ b ＝1， c ＝2时，画出这个几何体从左面看到的 形状图.
解：（3）从左面看到的形状图有3列，从左到右每列小正方形的个数分别为3，1，2，形状图如图所示.