中考数学一轮复习满分突破(全国通用)专题24特殊的平行四边形-矩形(原卷版+解析)

这是一份中考数学一轮复习满分突破(全国通用)专题24特殊的平行四边形-矩形(原卷版+解析)，共64页。


【知识要点】
矩形的定义：有一个角是直角的平行四边形叫做矩形。
矩形的性质：1）矩形具有平行四边形的所有性质；
2）矩形的四个角都是直角；
3）对角线互相平分且相等；
4）矩形既是中心对称图形，也是轴对称图形。矩形的对称中心是矩形对角线的交点；矩形有两条对称轴，矩形的对称轴是过矩形对边中点的直线；矩形的对称轴过矩形的对称中心。
【推论】1）在直角三角形中斜边的中线，等于斜边的一半。
2）直角三角形中，30度角所对应的直角边等于斜边的一半。
矩形的判定：1) 有一个角是直角的平行四边形是矩形；
2）对角线相等的平行四边形是矩形；
3）有三个角是直角的四边形是矩形。
矩形的面积公式： 面积=长×宽
考查题型一 利用矩形的性质求解
典例1．(2023·贵州黔东南·统考中考真题）一块直角三角板按如图所示方式放置在一张长方形纸条上，若，则的度数为（ ）
A．28°B．56°C．36°D．62°
变式1-1．(2023·山东日照·统考中考真题）如图，矩形ABCD为一个正在倒水的水杯的截面图，杯中水面与CD的交点为E，当水杯底面BC与水平面的夹角为27°时，∠AED的大小为（ ）
A．27°B．53°C．57°D．63°
变式1-2．(2023·安徽·统考中考真题）两个矩形的位置如图所示，若，则（ ）
A．B．C．D．
变式1-3．(2023·内蒙古通辽·统考中考真题）如图，在矩形中，为上的点，，，则______．
变式1-4．(2023·湖北十堰·统考中考真题）“美丽乡村”建设使我市农村住宅旧貌变新颜，如图所示为一农村民居侧面截图，屋坡，分别架在墙体的点，处，且，侧面四边形为矩形，若测得，则_________．
变式1-5．(2023·广西贺州·统考中考真题）如图，在矩形中，，分别为，的中点，以为斜边作，，连接，．若，则________．
考查题型二 利用矩形的性质求线段长
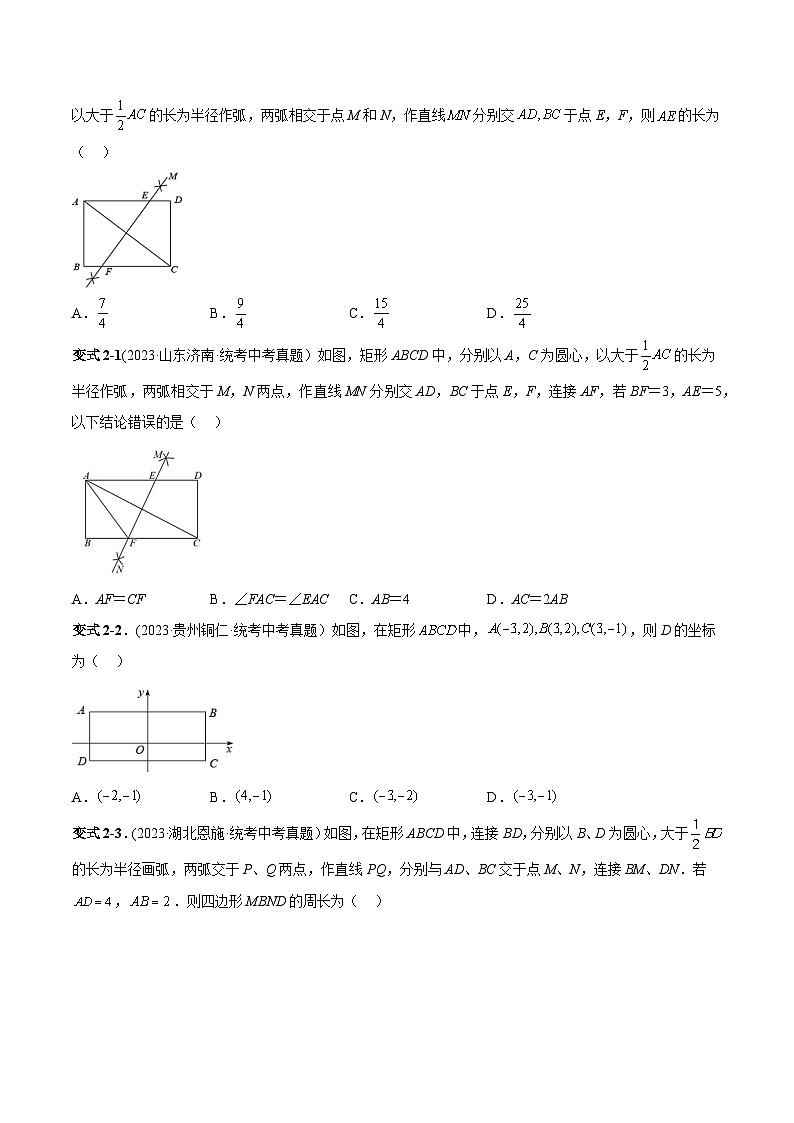
典例2．(2023·辽宁锦州·统考中考真题）如图，在矩形中，，分别以点A和C为圆心，以大于的长为半径作弧，两弧相交于点M和N，作直线分别交于点E，F，则的长为（ ）
A．B．C．D．
变式2-1(2023·山东济南·统考中考真题）如图，矩形ABCD中，分别以A，C为圆心，以大于的长为半径作弧，两弧相交于M，N两点，作直线MN分别交AD，BC于点E，F，连接AF，若BF＝3，AE＝5，以下结论错误的是（ ）
A．AF＝CFB．∠FAC＝∠EACC．AB＝4D．AC＝2AB
变式2-2．(2023·贵州铜仁·统考中考真题）如图，在矩形中，，则D的坐标为（ ）
A．B．C．D．
变式2-3．(2023·湖北恩施·统考中考真题）如图，在矩形ABCD中，连接BD，分别以B、D为圆心，大于的长为半径画弧，两弧交于P、Q两点，作直线PQ，分别与AD、BC交于点M、N，连接BM、DN．若，．则四边形MBND的周长为（ ）
A．B．5C．10D．20
变式2-4．(2023·四川攀枝花·统考中考真题）如图，在矩形中，，，点E、F分别为、的中点，、相交于点G，过点E作，交于点H，则线段的长度是（ ）
A．B．1C．D．
变式2-5．(2023·山东枣庄·统考中考真题）如图，在矩形ABCD中，按以下步骤作图：①分别以点B和D为圆心，以大于BD的长为半径作弧，两弧相交于点E和F；②作直线EF分别与DC，DB，AB交于点M，O，N．若DM＝5，CM＝3，则MN＝_____．
变式2-6．(2023·四川内江·统考中考真题）如图，矩形ABCD中，AB＝6，AD＝4，点E、F分别是AB、DC上的动点，EF∥BC，则AF+CE的最小值是 _____．
变式2-7．(2023·吉林·统考中考真题）如图，在矩形中，对角线，相交于点，点是边的中点，点在对角线上，且，连接．若，则__________．
变式2-8．(2023·青海西宁·统考中考真题）如图，在矩形中，E为的中点，连接，过点E作的垂线交于点F，交CD的延长线于点G，连接CF．已知，，则_________．
变式2-9．(2023·辽宁锦州·统考中考真题）如图，在矩形ABCD中，AB＝6，BC＝10，以点B为圆心、BC的长为半径画弧交AD于点E，再分别以点C，E为圆心、大于CE的长为半径画弧，两弧交于点F，作射线BF交CD于点G，则CG的长为__________________．
变式2-10．(2023·贵州安顺·统考中考真题）如图，在矩形中，点在上，，且，垂足为．
（1）求证：；
（2）若，求四边形的面积．
考查题型三 利用矩形的性质求面积
典例3．(2023·浙江台州·统考中考真题）一个垃圾填埋场，它在地面上的形状为长，宽的矩形，有污水从该矩形的四周边界向外渗透了，则该垃圾填埋场外围受污染土地的面积为（ ）
A．B．C．D．
变式3-1．(2023·湖南邵阳·统考中考真题）已知矩形的一边长为，一条对角线的长为，则矩形的面积为_________．
变式3-2．(2023·江苏徐州·统考中考真题）如图，四边形与均为矩形，点分别在线段上．若，矩形的周长为，则图中阴影部分的面积为___________．
变式3-3．(2023·重庆·统考中考真题）如图，在矩形中，，，以B为圆心，的长为半径画弧，交于点E．则图中阴影部分的面积为_________．（结果保留）
变式3-4．(2023·辽宁阜新·统考中考真题）如图，在矩形中，是边上一点，且，与相交于点，若的面积是，则的面积是______．
变式3-5．(2023·湖南湘潭·统考中考真题）为落实国家《关于全面加强新时代大中小学劳动教育的意见》，某校准备在校园里利用围墙（墙长）和长的篱笆墙，围成Ⅰ、Ⅱ两块矩形劳动实践基地．某数学兴趣小组设计了两种方案（除围墙外，实线部分为篱笆墙，且不浪费篱笆墙），请根据设计方案回答下列问题：
(1)方案一：如图①，全部利用围墙的长度，但要在Ⅰ区中留一个宽度的水池且需保证总种植面积为，试分别确定、的长；
(2)方案二：如图②，使围成的两块矩形总种植面积最大，请问应设计为多长？此时最大面积为多少？
考查题型四 利用矩形的性质证明
典例4(2023·重庆·统考中考真题）我们知道，矩形的面积等于这个矩形的长乘宽，小明想用其验证一个底为a，高为h的三角形的面积公式为．想法是：以为边作矩形，点A在边上，再过点A作的垂线，将其转化为证三角形全等，由全等图形面积相等来得到验证．按以上思路完成下面的作图与填空：证明：用直尺和圆规过点A作的垂线交于点D．（只保留作图痕迹）
在和中，
∵，
∴．
∵，
∴______①____．
∵，
∴______②_____．
又∵____③______．
∴（）．
同理可得：_____④______．
．
变式4-1．(2023·山西·中考真题）如图，在矩形ABCD中，AC是对角线．
(1)实践与操作：利用尺规作线段AC的垂直平分线，垂足为点O，交边AD于点E，交边BC于点F（要求：尺规作图并保留作图痕迹，不写作法，标明字母），
(2)猜想与证明：试猜想线段AE与CF的数量关系，并加以证明．
变式4-2(2023·山东威海·统考中考真题）如图:
(1)将两张长为8，宽为4的矩形纸片如图1叠放．
①判断四边形AGCH的形状，并说明理由；
②求四边形AGCH的面积．
(2)如图2，在矩形ABCD和矩形AFCE中，AB＝2，BC＝7，CF＝，求四边形AGCH的面积．
考查题型五 矩形折叠问题
典例5．(2023·山东菏泽·统考中考真题）如图所示，将一矩形纸片沿AB折叠，已知，则（ ）
A．48°B．66°C．72°D．78°
变式5-1．(2023·贵州毕节·统考中考真题）矩形纸片中，E为的中点，连接，将沿折叠得到，连接．若，，则的长是（ ）
A．3B．C．D．
变式5-2．(2023·四川宜宾·统考中考真题）如图，在矩形纸片ABCD中，，，将沿BD折叠到位置，DE交AB于点F，则的值为（ ）
A．B．C．D．
变式5-3．(2023·辽宁营口·统考中考真题）如图，在矩形中，点M在边上，把沿直线折叠，使点B落在边上的点E处，连接，过点B作，垂足为F，若，则线段的长为（ ）
A．B．C．D．
变式5-4．(2023·贵州遵义·统考中考真题）如图，将矩形纸片ABCD的两个直角进行折叠，使CB，AD恰好落在对角线AC上，B′，D′分别是B，D的对应点，折痕分别为CF，AE．若AB＝4，BC＝3，则线段的长是（ ）
A．B．2C．D．1
变式5-5．(2023·四川巴中·统考中考真题）如图，矩形AOBC的顶点A、B在坐标轴上，点C的坐标是(﹣10，8)，点D在AC上，将BCD沿BD翻折，点C恰好落在OA边上点E处，则tan∠DBE等于（ ）
A．B．C．D．
变式5-6(2023·山东潍坊·中考真题）小莹按照如图所示的步骤折叠A4纸，折完后，发现折痕AB′与A4纸的长边AB恰好重合，那么A4纸的长AB与宽AD的比值为___________．
变式5-7．(2023·甘肃兰州·统考中考真题）如图，在矩形纸片ABCD中，点E在BC边上，将沿DE翻折得到，点F落在AE上．若，，则______cm．
变式5-8．(2023·四川雅安·统考中考真题）如图，把一张矩形纸片沿对角线折叠，若BC＝9，CD＝3，那么阴影部分的面积为 _____．
变式5-9．(2023·江苏徐州·统考中考真题）如图，将矩形纸片ABCD沿CE折叠，使点B落在边AD上的点F处．若点E在边AB上，AB＝3，BC＝5，则AE＝________．
变式5-10．(2023·浙江杭州·统考中考真题）如图是一张矩形纸片，点是对角线的中点，点在边上，把沿直线折叠，使点落在对角线上的点处，连接，．若，则_____度．
变式5-11．(2023·浙江丽水·统考中考真题）如图，将矩形纸片折叠，使点B与点D重合，点A落在点P处，折痕为．
(1)求证：；
(2)若，求的长．
变式5-12．(2023·湖北荆门·统考中考真题）如图，已知矩形ABCD中，AB＝8，BC＝x（0＜x＜8），将△ACB沿AC对折到△ACE的位置，AE和CD交于点F．
(1)求证：△CEF≌△ADF；
(2)求tan∠DAF的值（用含x的式子表示）．
考查题型六 添加一个条件判定矩形
典例6．(2023·陕西·统考中考真题）在下列条件中，能够判定为矩形的是（ ）
A．B．C．D．
变式6-1．(2023·广西河池·统考中考真题）已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是（ ）
A．∠A=∠BB．∠A=∠CC．AC=BDD．AB⊥BC
变式6-2．(2023·甘肃武威·统考中考真题）如图，在四边形中，，，在不添加任何辅助线的前提下，要想四边形成为一个矩形，只需添加的一个条件是_______________．
变式6-3．(2023·湖南益阳·统考中考真题）如图，已知四边形是平行四边形，从①，②，③中选择一个作为条件，补充后使四边形成为菱形，则其选择是___（限填序号）．
变式6-4．(2023·黑龙江·统考中考真题）如图，在平行四边形中，对角线、相交于点O，在不添加任何辅助线的情况下，请你添加一个条件______________，使平行四边形是矩形．．

考查题型七 矩形的证明
典例7．(2023·湖北恩施·统考中考真题）如图，在四边形ABCD中，∠A=∠B=90°，AD=10cm，BC=8cm，点P从点D出发，以1cm/s的速度向点A运动，点M从点B同时出发，以相同的速度向点C运动，当其中一个动点到达端点时，两个动点同时停止运动．设点P的运动时间为t（单位：s），下列结论正确的是（ ）
A．当时，四边形ABMP为矩形
B．当时，四边形CDPM为平行四边形
C．当时，
D．当时，或6s
变式7-1．(2023·江苏无锡·统考中考真题）如图，D、E、F分别是各边中点，则以下说法错误的是（ ）
A．和的面积相等
B．四边形是平行四边形
C．若，则四边形是菱形
D．若，则四边形是矩形
变式7-2．(2023·四川遂宁·统考中考真题）如图，在菱形ABCD中，对角线AC、BD相交于点O，点E是AD的中点，连接OE，过点D作DF∥AC交OE的延长线于点F，连接AF．
(1)求证：≌；
(2)判定四边形AODF的形状并说明理由．
变式7-3．(2023·湖北十堰·统考中考真题）如图，中，，相交于点，，分别是，的中点．
(1)求证：；
(2)设，当为何值时，四边形是矩形？请说明理由．
变式7-4．(2023·上海·统考中考真题）已知：在圆O内，弦与弦交于点分别是和的中点，联结．
（1）求证：；
（2）联结，当时，求证：四边形为矩形．
考查题型八 矩形性质与判定综合
典例8．(2023·海南·统考中考真题）如图，菱形中，点E是边的中点，垂直交的延长线于点F，若，则菱形的边长是（ ）
A．3B．4C．5D．
变式8-1．(2023·湖南湘西·统考中考真题）如图，在Rt△ABC中，∠A＝90°，M为BC的中点，H为AB上一点，过点C作CG∥AB，交HM的延长线于点G，若AC＝8，AB＝6，则四边形ACGH周长的最小值是（ ）
A．24B．22C．20D．18
变式8-2．(2023·四川乐山·统考中考真题）如图，等腰△ABC的面积为2，AB=AC，BC=2．作AE∥BC且AE=BC．点P是线段AB上一动点，连接PE，过点E作PE的垂线交BC的延长线于点F，M是线段EF的中点．那么，当点P从A点运动到B点时，点M的运动路径长为（ ）
A．B．3C．D．4
变式8-3．(2023·四川自贡·统考中考真题）如图，矩形中，，是的中点，线段在边上左右滑动；若，则的最小值为____________．
变式8-4．(2023·湖南娄底·统考中考真题）九年级融融陪同父母选购家装木地板，她感觉某品牌木地板拼接图（如实物图）比较美观，通过手绘（如图）、测量、计算发现点是的黄金分割点，即．延长与相交于点，则________.（精确到0.001）

专题24 特殊的平行四边形-矩形
【考查题型】
【知识要点】
矩形的定义：有一个角是直角的平行四边形叫做矩形。
矩形的性质：1）矩形具有平行四边形的所有性质；
2）矩形的四个角都是直角；
3）对角线互相平分且相等；
4）矩形既是中心对称图形，也是轴对称图形。矩形的对称中心是矩形对角线的交点；矩形有两条对称轴，矩形的对称轴是过矩形对边中点的直线；矩形的对称轴过矩形的对称中心。
【推论】1）在直角三角形中斜边的中线，等于斜边的一半。
2）直角三角形中，30度角所对应的直角边等于斜边的一半。
矩形的判定：1) 有一个角是直角的平行四边形是矩形；
2）对角线相等的平行四边形是矩形；
3）有三个角是直角的四边形是矩形。
矩形的面积公式： 面积=长×宽
考查题型一 利用矩形的性质求解
典例1．(2023·贵州黔东南·统考中考真题）一块直角三角板按如图所示方式放置在一张长方形纸条上，若，则的度数为（ ）
A．28°B．56°C．36°D．62°
答案:D
分析：根据矩形的性质得出EF∥GH，过点C作CA∥EF，利用平行线的性质得出∠2=∠MCA，∠1=CAN，然后代入求解即可．
【详解】解：如图所示标注字母，
∵四边形EGHF为矩形，
∴EF∥GH，
过点C作CA∥EF，
∴CA∥EF∥GH，
∴∠2=∠MCA，∠1=∠NCA，
∵∠1=28°，∠MCN=90°，
∴∠2=∠MCA=90°-∠1=62°，
故选：D．
【点睛】题目主要考查矩形的性质，平行线的性质，角度的计算等，理解题意，作出相应辅助线是解题关键．
变式1-1．(2023·山东日照·统考中考真题）如图，矩形ABCD为一个正在倒水的水杯的截面图，杯中水面与CD的交点为E，当水杯底面BC与水平面的夹角为27°时，∠AED的大小为（ ）
A．27°B．53°C．57°D．63°
答案:D
分析：根据题意可知AE//BF，∠EAB=∠ABF，∠ABF+27°=90°，等量代换求出∠EAB，再根据平行线的性质求出∠AED．
【详解】解：如图所示：
∵AE//BF，
∴∠EAB=∠ABF，
∵四边形ABCD是矩形，
∴AB//CD，∠ABC=90°，
∴∠ABF+27°=90°，
∴∠ABF=63°，
∴∠EAB=63°，
∵AB//CD，
∴∠AED=∠EAB=63°．
故选：D．
【点睛】本题考查了矩形的性质，平行线的性质，熟记矩形的性质并灵活运用是解题的关键．矩形的性质：①平行四边形的性质矩形都具有； ②角：矩形的四个角都是直角；③边：邻边垂直；④对角线：矩形的对角线相等．
变式1-2．(2023·安徽·统考中考真题）两个矩形的位置如图所示，若，则（ ）
A．B．C．D．
答案:C
分析：用三角形外角性质得到∠3=∠1-90°=α-90°，用余角的定义得到∠2=90°-∠3=180°-α．
【详解】解：如图，∠3=∠1-90°=α-90°，
∠2=90°-∠3=180°-α．
故选：C．
【点睛】 本题主要考查了矩形，三角形外角，余角，解决问题的关键是熟练掌握矩形的角的性质，三角形的外角性质，互为余角的定义．
变式1-3．(2023·内蒙古通辽·统考中考真题）如图，在矩形中，为上的点，，，则______．
答案:##
【详解】解：设，
在矩形中，为上的点，，，
，
，
，
故答案为：．
【点睛】本题考查了矩形的性质，勾股定理，求正切，掌握正确的定义是解题的关键．
变式1-4．(2023·湖北十堰·统考中考真题）“美丽乡村”建设使我市农村住宅旧貌变新颜，如图所示为一农村民居侧面截图，屋坡，分别架在墙体的点，处，且，侧面四边形为矩形，若测得，则_________．
答案:
分析：根据矩形的性质可得，求出，根据等边对等角可得，然后根据三角形内角和定理即可求解．
【详解】四边形为矩形
，
故答案为：．
【点睛】本题考查了矩形的性质，等边对等角，三角形内角和定理，掌握以上知识是解题的关键．
变式1-5．(2023·广西贺州·统考中考真题）如图，在矩形中，，分别为，的中点，以为斜边作，，连接，．若，则________．
答案:
分析：根据矩形及等腰三角形的性质先求出，再利用中点定义及矩形性质可得，则可求出，，即可求得结果．
【详解】解：∵四边形是矩形，
∴，．
∵，，
∴．
∴．
∵，分别为，的中点，
∴，．
∵，
∴．
∴，．
∴．
故答案为：．
【点睛】此题考查了矩形的性质、等腰三角形的性质等知识，熟练掌握矩形与等腰三角形的性质是解答此题的关键．
考查题型二 利用矩形的性质求线段长
典例2．(2023·辽宁锦州·统考中考真题）如图，在矩形中，，分别以点A和C为圆心，以大于的长为半径作弧，两弧相交于点M和N，作直线分别交于点E，F，则的长为（ ）
A．B．C．D．
答案:D
分析：根据矩形可知为直角三角形，根据勾股定理可得的长度，在中得到，又由题知为的垂直平分线，于是 ，于是在中，利用锐角三角函数即可求出的长．
【详解】解：设与的交点为，
四边形为矩形，
，，，
为直角三角形，
，，
，
，
又由作图知为的垂直平分线，
，，
在中，
，
，
，
．
故选：D．
【点睛】本题主要考查矩形的性质，锐角三角函数，垂直平分线，勾股定理，掌握定理以及性质是解题的关键．
变式2-1(2023·山东济南·统考中考真题）如图，矩形ABCD中，分别以A，C为圆心，以大于的长为半径作弧，两弧相交于M，N两点，作直线MN分别交AD，BC于点E，F，连接AF，若BF＝3，AE＝5，以下结论错误的是（ ）
A．AF＝CFB．∠FAC＝∠EACC．AB＝4D．AC＝2AB
答案:D
分析：根据作图过程可得，是的垂直平分线，再由矩形的性质可以证明，可得再根据勾股定理可得AB的长，即可判定得出结论．
【详解】解：A，根据作图过程可得，是的垂直平分线，
故此选项不符合题意．
B，如图，
由矩形的性质可以证明，
∵是的垂直平分线，
故此选项不符合题意．
C，
在中
故此选项不符合题意．
D，
故此选项符合题意．
故选：D．
【点睛】本题考查了作图-基本作图，线段垂直平分线的性质、矩形的性质、勾股定理，解决本题的关键是掌握基本作图方法．
变式2-2．(2023·贵州铜仁·统考中考真题）如图，在矩形中，，则D的坐标为（ ）
A．B．C．D．
答案:D
分析：先根据A、B的坐标求出AB的长，则CD=AB=6，并证明轴，同理可得轴，由此即可得到答案．
【详解】解：∵A（-3，2），B（3，2），
∴AB=6，轴，
∵四边形ABCD是矩形，
∴CD=AB=6，轴，
同理可得轴，
∵点C（3，-1），
∴点D的坐标为（-3，-1），
故选D．
【点睛】本题主要考查了坐标与图形，矩形的性质，熟知矩形的性质是解题的关键．
变式2-3．(2023·湖北恩施·统考中考真题）如图，在矩形ABCD中，连接BD，分别以B、D为圆心，大于的长为半径画弧，两弧交于P、Q两点，作直线PQ，分别与AD、BC交于点M、N，连接BM、DN．若，．则四边形MBND的周长为（ ）
A．B．5C．10D．20
答案:C
分析：先根据矩形的性质可得，再根据线段垂直平分线的性质可得，根据等腰三角形的性质可得，从而可得，根据平行线的判定可得，然后根据菱形的判定可得四边形是菱形，设，则，在中，利用勾股定理可得的值，最后根据菱形的周长公式即可得．
【详解】解：四边形是矩形，
，
，
由作图过程可知，垂直平分，
，
，
，
，
四边形是平行四边形，
又，
平行四边形是菱形，
设，则，
在中，，即，
解得，
则四边形的周长为，
故选：C．
【点睛】本题考查了矩形的性质、菱形的判定与性质、勾股定理、线段垂直平分线等知识点，熟练掌握菱形的判定与性质是解题关键．
变式2-4．(2023·四川攀枝花·统考中考真题）如图，在矩形中，，，点E、F分别为、的中点，、相交于点G，过点E作，交于点H，则线段的长度是（ ）
A．B．1C．D．
答案:A
分析：根据矩形的性质得出，求出，，求出，根据勾股定理求出，求出，根据三角形的中位线求出，根据相似三角形的判定得出，根据相似三角形的性质得出，再求出答案即可．
【详解】解析：四边形是矩形，，，
，，，
点E、F分别为、的中点，
，，
，
，
，
．
由勾股定理得：，
，
，
，
，
，
解得：，
故选：A．
【点睛】本题考查了矩形的性质和相似三角形的性质和判定，能熟记矩形的性质是解此题的关键．
变式2-5．(2023·山东枣庄·统考中考真题）如图，在矩形ABCD中，按以下步骤作图：①分别以点B和D为圆心，以大于BD的长为半径作弧，两弧相交于点E和F；②作直线EF分别与DC，DB，AB交于点M，O，N．若DM＝5，CM＝3，则MN＝_____．
答案:
分析：作辅助线，利用垂直平分线的性质得出的值，OB＝OD，由矩形的性质、勾股定理得出，的值，进而得出，的值，根据全等三角形的判定（角边角）得出△MDO≌△BNO，最后利用全等三角形的性质得出结论．
【详解】解：如图，连接BM．
由作图可知MN垂直平分线段BD，
∴BM＝DM＝5．
∵四边形ABCD是矩形，
∴∠C＝90°，CD∥AB．
∴BC＝＝＝4．
∴BD＝＝＝．
∴OB＝OD＝．
∵∠MOD＝90°，
∴OM＝＝＝．
∵CD∥AB，
∴∠MDO＝∠NBO．
在△MDO和△NBO中，
∴△MDO≌△BNO（ASA）．
∴OM＝ON＝．
∴MN＝．
故答案为：．
【点睛】本题考查线段的垂直平分线的性质，作图—基本作图，勾股定理，全等三角形的判定与性质等的理解与运用能力．线段的垂直平分线上的点到线段的两个端点的距离相等．两个三角形的两个角和它们的夹边对应相等的两三角形全等；两全等三角形的对应边相等，对应角相等．在一个直角三角形中，两个直角边边长的平方加起来等于斜边长的平方．掌握线段的垂直平分线的性质是解本题的关键．
变式2-6．(2023·四川内江·统考中考真题）如图，矩形ABCD中，AB＝6，AD＝4，点E、F分别是AB、DC上的动点，EF∥BC，则AF+CE的最小值是 _____．
答案:10
分析：延长BC到G，使CG＝EF，连接FG，证明四边形EFGC是平行四边形，得出CE＝FG，得出当点A、F、G三点共线时，AF+CE的值最小，根据勾股定理求出AG即可．
【详解】解：延长BC到G，使CG＝EF，连接FG，
∵，EF＝CG，
∴四边形EFGC是平行四边形，
∴CE＝FG，
∴AF+CE＝AF+FG，
∴当点A、F、G三点共线时，AF+CE的值最小为AG，
由勾股定理得，AG＝＝＝10，
∴AF+CE的最小值为10，
故答案为：10．
【点睛】本题主要考查了勾股定理，平行四边形的判定和性质，根据题意作出辅助线，得出当A、F、G三点共线时，AF+CE的值最小，是解题的关键．
变式2-7．(2023·吉林·统考中考真题）如图，在矩形中，对角线，相交于点，点是边的中点，点在对角线上，且，连接．若，则__________．
答案:##2.5
分析：由矩形的性质可得点F是OA的中点，从而EF是△AOD的中位线，则由三角形中位线定理即可求得EF的长．
【详解】∵四边形ABCD是矩形，
∴BD=AC=10，OA=AC，OD=BD=5，
∵，
∴，即点F是OA的中点．
∵点是边的中点，
∴EF是△AOD的中位线，
∴．
故答案为：．
【点睛】本题考查了矩形的性质，三角形中位线定理等知识，掌握中位线定理是本题的关键．
变式2-8．(2023·青海西宁·统考中考真题）如图，在矩形中，E为的中点，连接，过点E作的垂线交于点F，交CD的延长线于点G，连接CF．已知，，则_________．
答案:
分析：由题意，先证明△AEF≌△DEG，则EF=EG，，利用等腰三角形的性质，求出，然后得到AB=CD=，则，利用勾股定理求出BC，然后得到AE的长度，即可求出FE的长度．
【详解】解：根据题意，在矩形中，则
AB=CD，BC=AD，∠A=∠EDG=90°，
∵E为的中点，
∴AE=DE，
∵∠AEF=∠DEG，
∴△AEF≌△DEG，
∴EF=EG，；
∵CE⊥FG，
∴，
∴AB=CD=，
∴，
在直角△BCF中，由勾股定理则
，
∴AD=3，
∴，
在直角△AEF中，由勾股定理则
；
故答案为：．
【点睛】本题考查了矩形的性质，全等三角形的判定和性质，垂直平分线的性质，勾股定理等知识，解题的关键是熟练掌握所学的知识，正确得到．
变式2-9．(2023·辽宁锦州·统考中考真题）如图，在矩形ABCD中，AB＝6，BC＝10，以点B为圆心、BC的长为半径画弧交AD于点E，再分别以点C，E为圆心、大于CE的长为半径画弧，两弧交于点F，作射线BF交CD于点G，则CG的长为__________________．
答案:
分析：根据作图过程可得BF是∠EBC的平分线，然后证明△EBG≌△CBG，再利用勾股定理即可求出CG的长．
【详解】解：如图，连接EG，
根据作图过程可知：BF是∠EBC的平分线，
∴∠EBG＝∠CBG，
在△EBG和△CBG中，
，
∴△EBG≌△CBG（SAS），
∴GE＝GC，∠BEG=∠C=90°，
在Rt△ABE中，AB＝6，BE＝BC＝10，
∴AE＝＝8，
∴DE＝AD﹣AE＝10﹣8＝2，
在Rt△DGE中，DE＝2，DG＝DC﹣CG＝6﹣CG，EG＝CG，
∴EG2﹣DE2＝DG2
∴CG2﹣22＝（6﹣CG）2，
解得CG＝．
故答案为：．
【点睛】本题考查了矩形的性质，作图-基本作图，解决本题的关键是掌握矩形的性质．
变式2-10．(2023·贵州安顺·统考中考真题）如图，在矩形中，点在上，，且，垂足为．
（1）求证：；
（2）若，求四边形的面积．
答案:（1）见详解；（2）4-8
分析：（1）由矩形的性质可得∠D=90°，AB∥CD，从而得∠D=∠ANB，∠BAN=∠AMD，进而即可得到结论；
（2）由以及勾股定理得AN=DM=4，AB=，进而即可求解．
【详解】（1）证明：∵在矩形中，
∴∠D=90°，AB∥CD，
∴∠BAN=∠AMD，
∵，
∴∠ANB=90°，即：∠D=∠ANB，
又∵，
∴（AAS），
（2）∵，
∴AN=DM=4，
∵，
∴，
∴AB=，
∴矩形的面积=×2=4，
又∵，
∴四边形的面积=4-4-4=4-8．
【点睛】本题主要考查矩形的性质，勾股定理，全等三角形的判定和性质，熟练掌握AAS证明三角形全等，是解题的关键．
考查题型三 利用矩形的性质求面积
典例3．(2023·浙江台州·统考中考真题）一个垃圾填埋场，它在地面上的形状为长，宽的矩形，有污水从该矩形的四周边界向外渗透了，则该垃圾填埋场外围受污染土地的面积为（ ）
A．B．C．D．
答案:B
分析：根据题意可知受污染土地由两类长分别为，，宽分别为的矩形，及四个能组成一个以半径为的圆组成，求出面积和即可．
【详解】解：根据题意可知受污染土地由两类长分别为，，宽分别为的矩形，及四个能组成一个以半径为的圆组成，
面积为：，
故选：B．
【点睛】本题考查了矩形的面积，圆的面积的求法，解题的关键是读懂题目，明确所求的面积的组成部分为哪些．
变式3-1．(2023·湖南邵阳·统考中考真题）已知矩形的一边长为，一条对角线的长为，则矩形的面积为_________．
答案:48
分析：如图，先根据勾股定理求出，再由求解即可．
【详解】解：在矩形ABCD中，，，

∴在中，(cm)，
∴．
故答案为：48．
【点睛】此题考查了矩形的性质，勾股定理，解题的关键是熟知上述知识．
变式3-2．(2023·江苏徐州·统考中考真题）如图，四边形与均为矩形，点分别在线段上．若，矩形的周长为，则图中阴影部分的面积为___________．
答案:
分析：根据矩形性质和矩形周长，得到，然后设，然后根据列出代数式即可求解阴影部分面积．
【详解】∵矩形的周长为，
∴，
设，则，，，
，
故答案为．
【点睛】本题考查了矩形的性质，和列代数式及整式的化简，关键是读懂题目，列出代数式．
变式3-3．(2023·重庆·统考中考真题）如图，在矩形中，，，以B为圆心，的长为半径画弧，交于点E．则图中阴影部分的面积为_________．（结果保留）
答案:
分析：先根据特殊角的锐角三角函数值，求出，进而求出，再根据扇形的面积公式求解即可．
【详解】解：∵矩形，
，
以B为圆心，的长为半轻画弧，交于点E， ，
，
在中，，
，
，
，
S阴影 ．
故答案为： ．
【点睛】本题考查了由特殊角的三角函数值求角度数，矩形的性质，扇形的面积的计算，综合掌握以上知识点并熟练运用是解题的关键．
变式3-4．(2023·辽宁阜新·统考中考真题）如图，在矩形中，是边上一点，且，与相交于点，若的面积是，则的面积是______．
答案:27
分析：根据矩形的性质，很容易证明∽，相似三角形之比等于对应边比的平方，即可求出的面积．
【详解】解：四边形是矩形，
，
，
，
∽，
，，
：：，
：：，即：：，
．
故答案为：．
【点睛】本题考查了相似三角形的判定与性质，矩形的性质，综合性比较强，学生要灵活应用．掌握相似三角形的面积比是相似比的平方是解题的关键．
变式3-5．(2023·湖南湘潭·统考中考真题）为落实国家《关于全面加强新时代大中小学劳动教育的意见》，某校准备在校园里利用围墙（墙长）和长的篱笆墙，围成Ⅰ、Ⅱ两块矩形劳动实践基地．某数学兴趣小组设计了两种方案（除围墙外，实线部分为篱笆墙，且不浪费篱笆墙），请根据设计方案回答下列问题：
(1)方案一：如图①，全部利用围墙的长度，但要在Ⅰ区中留一个宽度的水池且需保证总种植面积为，试分别确定、的长；
(2)方案二：如图②，使围成的两块矩形总种植面积最大，请问应设计为多长？此时最大面积为多少？
答案:(1)CG长为8m，DG长为4m
(2)当BC=m时，围成的两块矩形总种植面积最大=m2
分析：（1）两块篱笆墙的长为12m，篱笆墙的宽为AD=GH=BC=(21-12)÷3=3m，设CG为am，DG为(12-a)m，再由矩形面积公式求解；
（2）设两块矩形总种植面积为y， BC长为xm，那么AD=HG=BC=xm，DC=(21-3x)m，由题意得，围成的两块矩形总种植面积最大=BC×DC，代入有关数据再把二次函数化成顶点式即可 .
【详解】（1）解：两块篱笆墙的长为12m，篱笆墙的宽为AD=GH=BC=(21-12)÷3=3m，
设CG为am，DG为(12-a)m，那么
AD×DC-AE×AH=32
即12×3-1×（12-a）=32
解得：a=8
∴CG=8m，DG=4m．
（2）解：设两块矩形总种植面积为ym2，BC长为xm，那么AD=HG=BC=xm，DC=(21-3x)m，由题意得，
两块矩形总种植面积=BC×DC
即y=x·(21-3x)
∴y=-3x2+21x
=-3(x-)2+
∵21-3x≤12
∴x≥3
∴当BC=m时，y最大=m2．
【点睛】此题考查了二次函数的实际应用，解题的关键是正确理解题意找到等量关系列出方程．
考查题型四 利用矩形的性质证明
典例4(2023·重庆·统考中考真题）我们知道，矩形的面积等于这个矩形的长乘宽，小明想用其验证一个底为a，高为h的三角形的面积公式为．想法是：以为边作矩形，点A在边上，再过点A作的垂线，将其转化为证三角形全等，由全等图形面积相等来得到验证．按以上思路完成下面的作图与填空：证明：用直尺和圆规过点A作的垂线交于点D．（只保留作图痕迹）
在和中，
∵，
∴．
∵，
∴______①____．
∵，
∴______②_____．
又∵____③______．
∴（）．
同理可得：_____④______．
．
答案:图见解析，∠ADC=∠F；∠1=∠2；AC=AC；△ABD≌△BAE
分析：根据垂线的作图方法作图即可，利用垂直的定义得到∠ADC=∠F，根据平行线的性质得到∠1=∠2，即可证明△ADC≌△CAF，同理可得△ABD≌△BAE，由此得到结论．
【详解】解：如图，AD即为所求，
在和中，
∵，
∴．
∵，
∴∠ADC=∠F．
∵，
∴∠1=∠2．
又∵AC=AC．
∴（）．
同理可得：△ABD≌△BAE．
．
故答案为：∠ADC=∠F；∠1=∠2；AC=AC；△ABD≌△BAE．
【点睛】此题考查了全等三角形的判定及性质，垂线的作图方法，矩形的性质，熟练掌握三角形的判定定理是解题的关键．
变式4-1．(2023·山西·中考真题）如图，在矩形ABCD中，AC是对角线．
(1)实践与操作：利用尺规作线段AC的垂直平分线，垂足为点O，交边AD于点E，交边BC于点F（要求：尺规作图并保留作图痕迹，不写作法，标明字母），
(2)猜想与证明：试猜想线段AE与CF的数量关系，并加以证明．
答案:(1)作图见解析
(2)，证明见解析
分析：（1）根据垂直平分线的尺规作图的画法，分别以A、C为圆心，以大于AC的长为半径画弧，交于两点，过两点作直线即可得到线段AC的垂直平分线．
（2）利用矩形及垂直平分线的性质，可以证得，根据全等三角形的性质即可得出结论．
【详解】（1）解：如图，
（2）解：．证明如下：
∵四边形ABCD是矩形，
∴ ．
∴．
∵EF为AC的垂直平分线，
∴．
∴．
∴．
【点睛】本题主要考查了垂直平分线的尺规作图的画法、矩形的性质、全等三角形的判定和性质．
变式4-2(2023·山东威海·统考中考真题）如图:
(1)将两张长为8，宽为4的矩形纸片如图1叠放．
①判断四边形AGCH的形状，并说明理由；
②求四边形AGCH的面积．
(2)如图2，在矩形ABCD和矩形AFCE中，AB＝2，BC＝7，CF＝，求四边形AGCH的面积．
答案:(1)①菱形，理由见解析；②20
(2)
分析：（1）①根据邻边相等的平行四边形是菱形证明即可；②设AH=CG=x，利用勾股定理构建方程即可解决问题；
（2）两个矩形的对角线相等，可得出EC的长，设AH=CG=x，利用勾股定理以及边长之间的关系可得出x的值，进而可求出面积．
（1）
①∵四边形ABCD，四边形AECF都是矩形
∴
∴四边形AHCG为平行四边形
∵
∴
∴
∴四边形AHCG为菱形；
②设AH=CG=x，则DH=AD-AH=8-x
在中
即
解得
∴四边形AHCG的面积为；
（2）
由图可得矩形ABCD和矩形AFCE对角线相等
∴
∴
设AH=CG=x则HD=7-x
在中，
在中，
∵EC=EH+CH=8
∴x=3
∴四边形AGCH的面积为．
【点睛】本题考查了矩形的性质，菱形的判定和性质，解直角三角形等知识，解题的关键是学会利用参数构建方程解决问题．
考查题型五 矩形折叠问题
典例5．(2023·山东菏泽·统考中考真题）如图所示，将一矩形纸片沿AB折叠，已知，则（ ）
A．48°B．66°C．72°D．78°
答案:C
分析：由折叠及矩形的性质可得，再根据平行线的性质求出，根据周角的定义求解即可．
【详解】∵将一矩形纸片沿AB折叠，
∴，
，
，
，
，
故选：C．
【点睛】本题考查了矩形的性质，折叠的性质及平行线的性质，熟练掌握知识点是解题的关键．
变式5-1．(2023·贵州毕节·统考中考真题）矩形纸片中，E为的中点，连接，将沿折叠得到，连接．若，，则的长是（ ）
A．3B．C．D．
答案:D
分析：连接BF交AE于点G，根据对称的性质，可得AE垂直平分BF，BE=FE，BG=FG=，根据E为BC中点，可证BE=CE=EF，通过等边对等角可证明∠BFC=90°，利用勾股定理求出AE，再利用三角函数（或相似）求出BF，则根据计算即可．
【详解】连接BF，与AE相交于点G，如图，
∵将沿折叠得到
∴与关于AE对称
∴AE垂直平分BF，BE=FE，BG=FG=
∵点E是BC中点
∴BE=CE=DF=
∴
∵
∴
∴
∵BE=CE=DF
∴∠EBF=∠EFB，∠EFC=∠ECF
∴∠BFC=∠EFB+∠EFC=
∴
故选 D
【点睛】本题考查了折叠对称的性质，熟练运用对称性质证明相关线段相等是解题的关键．
变式5-2．(2023·四川宜宾·统考中考真题）如图，在矩形纸片ABCD中，，，将沿BD折叠到位置，DE交AB于点F，则的值为（ ）
A．B．C．D．
答案:C
分析：先根据矩形的性质和折叠的性质，利用“AAS”证明，得出，，设，则，根据勾股定理列出关于x的方程，解方程得出x的值，最后根据余弦函数的定义求出结果即可．
【详解】解：∵四边形ABCD为矩形，
∴CD=AB=5，AB=BC=3，，
根据折叠可知，，，，
∴在△AFD和△EFB中，
∴（AAS），
∴，，
设，则，
在中，，
即，
解得：，则，
∴，故C正确．
故选：C．
【点睛】本题主要考查了矩形的折叠问题，三角形全等的判定和性质，勾股定理，三角函数的定义，根据题意证明，是解题的关键．
变式5-3．(2023·辽宁营口·统考中考真题）如图，在矩形中，点M在边上，把沿直线折叠，使点B落在边上的点E处，连接，过点B作，垂足为F，若，则线段的长为（ ）
A．B．C．D．
答案:A
分析：先证明△BFC≌△CDE，可得DE=CF=2，再用勾股定理求得CE=，从而可得AD=BC=，最后求得AE的长．
【详解】解：∵四边形ABCD是矩形，
∴BC=AD，∠ABC=∠D=90°，AD∥BC，
∴∠DEC=∠FCB，
∵，
∴∠BFC=∠CDE，
∵把沿直线折叠，使点B落在边上的点E处，
∴BC=EC，
在△BFC与△CDE中，
∴△BFC≌△CDE（AAS），
∴DE=CF=2，
∴，
∴AD=BC=CE=，
∴AE=AD-DE=，
故选：A．
【点睛】本题考查了矩形的性质、全等三角形的判定和性质、折叠的性质，勾股定理的应用，解决本题的关键是熟练掌握矩形中的折叠问题．
变式5-4．(2023·贵州遵义·统考中考真题）如图，将矩形纸片ABCD的两个直角进行折叠，使CB，AD恰好落在对角线AC上，B′，D′分别是B，D的对应点，折痕分别为CF，AE．若AB＝4，BC＝3，则线段的长是（ ）
A．B．2C．D．1
答案:D
分析：先利用矩形的性质与勾股定理求解 再利用轴对称的性质求解，从而可得答案.
【详解】解： 矩形纸片ABCD，


由折叠可得：

同理：

故选：
【点睛】本题考查的是勾股定理的应用，轴对称的性质，矩形的性质，掌握以上知识是解题的关键.
变式5-5．(2023·四川巴中·统考中考真题）如图，矩形AOBC的顶点A、B在坐标轴上，点C的坐标是(﹣10，8)，点D在AC上，将BCD沿BD翻折，点C恰好落在OA边上点E处，则tan∠DBE等于（ ）
A．B．C．D．
答案:D
分析：先根据四边形ABCD是矩形，C（-10，8），得出BC=AO=10，AC=OB=8，∠A=∠O=∠C=90°，再由折叠的性质得到CD=DE，BC=BE=10，∠DEB=∠C=90°，利用勾股定理先求出OE的长，即可得到AE，再利用勾股定理求出DE，利用求解即可.
【详解】解：∵四边形ABCD是矩形，C（-10，8），
∴BC=AO=10，AC=OB=8，∠A=∠O=∠C=90°，
由折叠的性质可知：CD=DE，BC=BE=10，∠DEB=∠C=90°，
在直角三角形BEO中：，
∴，
设，则
在直角三角形ADE中：，
∴，
解得，
∴，
∵∠DEB=90°，
∴，
故选D.
【点睛】本题主要考查了矩形的性质，折叠的性质，勾股定理，三角函数，解题的关键在于能够熟练掌握相关知识进行求解.
变式5-6(2023·山东潍坊·中考真题）小莹按照如图所示的步骤折叠A4纸，折完后，发现折痕AB′与A4纸的长边AB恰好重合，那么A4纸的长AB与宽AD的比值为___________．
答案:
分析：判定△AB′D′是等腰直角三角形，即可得出AB′=AD，再根据AB′= AB，再计算即可得到结论．
【详解】解：∵四边形ABCD是矩形，
∴∠D=∠B=∠DAB=90°，
由操作一可知：∠DAB′=∠D′AB′=45°，∠AD′B′=∠D=90°，AD=AD′，
∴△AB′D′是等腰直角三角形，
∴AD=AD′= B′D′，
由勾股定理得AB′=AD，
又由操作二可知：AB′=AB，
∴AD=AB，
∴=，
∴A4纸的长AB与宽AD的比值为．
故答案为：．
【点睛】本题主要考查了矩形的性质以及折叠变换的运用，解题的关键是理解题意，灵活运用所学知识解决问题．
变式5-7．(2023·甘肃兰州·统考中考真题）如图，在矩形纸片ABCD中，点E在BC边上，将沿DE翻折得到，点F落在AE上．若，，则______cm．
答案:
分析：由将△CDE沿DE翻折得到△FDE，点F落在AE上，可得EF=CE=3cm，CD=DF，∠DEC=∠DEF，由矩形的性质得∠DFE=∠C=90°=∠DFA，从而得AF=6cm，AD=AE=9cm，进而由勾股定理既可以求解。
【详解】解：∵将△CDE沿DE翻折得到△FDE，点F落在AE上，，四边形ABCD是矩形，
∴EF=CE=3cm，CD=DF，∠DEC=∠DEF，∠DFE=∠C=90°=∠DFA，
∵AF=2EF，
∴AF=6cm，
∴AE=AF+EF=6+3=9(cm)，
∵四边形ABCD是矩形，
∴AB=CD=DF，，
∴∠ADE=∠DEC=∠DEF，
∴AD=AE=9cm，
∵在Rt△ADF中，AF2+DF2=AD2
∴62+DF2=92，
∴DF= (cm)，
AB=DF= (cm)，
故答案为∶．
【点睛】本题考查矩形的性质、勾股定理及轴对称，熟练掌握轴对称的性质是解题的关键．
变式5-8．(2023·四川雅安·统考中考真题）如图，把一张矩形纸片沿对角线折叠，若BC＝9，CD＝3，那么阴影部分的面积为 _____．
答案:
分析：利用矩形与轴对称的性质先证明 再利用勾股定理求解 再利用三角形的面积公式可得答案．
【详解】解： 把一张矩形纸片沿对角线折叠，BC＝9，CD＝3，






解得：

故答案为：
【点睛】本题考查的是矩形的性质，轴对称的性质，勾股定理的应用，证明是解本题的关键．
变式5-9．(2023·江苏徐州·统考中考真题）如图，将矩形纸片ABCD沿CE折叠，使点B落在边AD上的点F处．若点E在边AB上，AB＝3，BC＝5，则AE＝________．
答案:##
分析：由折叠性质可得CF=BC=5，BE=EF，由矩形性质有CD=AB=3，BC=AD=5，勾股定理求得DF，AF．设BE=EF=x，则AE=AB-BE，在直角三角形AEF中，根据勾股定理，建立方程，解方程即可求解．
【详解】解：由折叠性质可得CF=BC=5，BE=EF，
由矩形性质有CD=AB=3，BC=AD=5，
∵∠D=90°，
∴，
所以，
所以 BE=EF=x，则AE=AB-BE=3-x，在直角三角形AEF中:
，
∴，
解得，
∴，
故答案为：．
【点睛】本题考查了图形折叠的性质，勾股定理，矩形的性质，在直角三角形AEF中运用勾股定理建立方程求解是关键．
变式5-10．(2023·浙江杭州·统考中考真题）如图是一张矩形纸片，点是对角线的中点，点在边上，把沿直线折叠，使点落在对角线上的点处，连接，．若，则_____度．
答案:18
分析：连接MD，设∠DAF=x，利用折叠与等腰三角形的性质，用x的代数式表示出∠ADC=90°，列出方程解方程即可．
【详解】连接MD，设∠DAF=x
根据矩形的基本性质可知AM=MD，AD∥BC，∠BCD=∠ADC=90°
∴∠MDA=∠DAF=x，∠ACB=∠DAC=x
∴∠DMF=2x
∵△DCE折叠得到△DFE
∴DF=CD=AB，DE⊥FC，∠FDE=∠CDE
又MF=AB
∴MF=DF
∴∠MDF=2x
∵∠BCD=∠ACB+∠ACD=90°，∠EDC+∠FCD=90°
∴∠CDE=∠ACD=x
∴∠FDE=∠CDE=x
∴∠ADC=∠ADM+∠MDF+∠FDE+∠CDE=x+2x+x+x=5x=90°
∴x=18°
故∠DAF=18°
故答案为18．
【点睛】本题考查了矩形的折叠问题，能够做出合适的辅助线用∠DAF表示出∠ADC是解题关键．
变式5-11．(2023·浙江丽水·统考中考真题）如图，将矩形纸片折叠，使点B与点D重合，点A落在点P处，折痕为．
(1)求证：；
(2)若，求的长．
答案:(1)证明见解析
(2)cm
分析：（1）利用ASA证明即可；
（2）过点E作EG⊥BC交于点G，求出FG的长，设AE=xcm，用x表示出DE的长，在Rt△PED中，由勾股定理求得答案．
（1）
∵四边形ABCD是矩形，
∴AB=CD，∠A=∠B=∠ADC=∠C=90°，
由折叠知，AB=PD，∠A=∠P，∠B=∠PDF=90°，
∴PD=CD，∠P=∠C，∠PDF =∠ADC，
∴∠PDF-∠EDF=∠ADC-∠EDF,
∴∠PDE=∠CDF，
在△PDE和△CDF中，
,
∴（ASA）；
（2）
如图，过点E作EG⊥BC交于点G，
∵四边形ABCD是矩形,
∴AB=CD=EG=4cm，
又∵EF=5cm，∴cm,
设AE=xcm，
∴EP=xcm，
由知，EP=CF=xcm，
∴DE=GC=GF+FC=3+x，
在Rt△PED中，,
即，
解得，，
∴BC=BG+GC= (cm）．
【点睛】本题考查了翻折变换，矩形的性质，勾股定理，全等三角形的判定和性质，根据翻折变换的性质将问题转化到直角三角形中利用勾股定理是解题的关键．
变式5-12．(2023·湖北荆门·统考中考真题）如图，已知矩形ABCD中，AB＝8，BC＝x（0＜x＜8），将△ACB沿AC对折到△ACE的位置，AE和CD交于点F．
(1)求证：△CEF≌△ADF；
(2)求tan∠DAF的值（用含x的式子表示）．
答案:(1)证明见解析
(2)tan∠DAF＝
分析：（1）根据矩形的性质得到∠B＝∠D＝90°，BC＝AD，根据折叠的性质得到BC＝CE，∠E＝∠B＝90°，等量代换得到∠E＝∠D＝90°，AD＝CE，根据AAS证明三角形全等即可；
（2）设DF＝a，则CF＝8﹣a，根据矩形的性质和折叠的性质证明AF＝CF＝8﹣a，在Rt△ADF中，根据勾股定理表示出DF的长，根据正切的定义即可得出答案．
【详解】（1）证明：∵四边形ABCD是矩形，
∴∠B＝∠D＝90°，BC＝AD，
根据折叠的性质得：BC＝CE，∠E＝∠B＝90°，
∴∠E＝∠D＝90°，AD＝CE，
在△CEF与△ADF中，
，
∴△CEF≌△ADF（AAS）；
（2）解：设DF＝a，则CF＝8﹣a，
∵四边形ABCD是矩形，
∴AB∥CD，AD＝BC＝x，
∴∠DCA＝∠BAC，
根据折叠的性质得：∠EAC＝∠BAC，
∴∠DCA＝∠EAC，
∴AF＝CF＝8﹣a，
在Rt△ADF中，
∵AD2+DF2＝AF2，
∴x2+a2＝（8﹣a）2，
∴a＝，
∴tan∠DAF＝＝．
【点睛】本题考查了锐角三角函数，全等三角形的判定与性质，矩形的性质，翻折变换（折叠问题），根据矩形的性质和折叠的性质证出AF＝CF是解题的关键．
考查题型六 添加一个条件判定矩形
典例6．(2023·陕西·统考中考真题）在下列条件中，能够判定为矩形的是（ ）
A．B．C．D．
答案:D
分析：根据矩形的判定定理逐项判断即可．
【详解】当AB=AC时，不能说明是矩形，所以A不符合题意；
当AC⊥BD时，是菱形，所以B不符合题意；
当AB=AD时，是菱形，所以C不符合题意；
当AC=BD时，是矩形，所以D符合题意．
故选：D．
【点睛】本题主要考查了矩形的判定，掌握判定定理是解题的关键．有一个角是直角的平行四边形是矩形；对角线相等的平行四边形是矩形．
变式6-1．(2023·广西河池·统考中考真题）已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是（ ）
A．∠A=∠BB．∠A=∠CC．AC=BDD．AB⊥BC
答案:B
分析：由矩形的判定方法依次判断即可得出结果．
【详解】解：A、∠A=∠B，∠A+∠B=180°，所以∠A=∠B=90°，可以判定这个平行四边形为矩形，不符合题意；
B、∠A=∠C不能判定这个平行四边形为矩形，符合题意；
C、AC=BD，对角线相等，可推出平行四边形ABCD是矩形，故不符合题意；
D、AB⊥BC，所以∠B=90°，可以判定这个平行四边形为矩形，不符合题意，
故选B．
【点睛】本题考查了矩形的判定，熟练掌握“有一个角是直角的平行四边形是矩形、对角线相等的平行四边形是矩形、有三个角是直角的四边形是矩形”是解题的关键．
变式6-2．(2023·甘肃武威·统考中考真题）如图，在四边形中，，，在不添加任何辅助线的前提下，要想四边形成为一个矩形，只需添加的一个条件是_______________．
答案:（答案不唯一）
分析：】先证四边形ABCD是平行四边形，再由矩形的判定即可得出结论．
【详解】解：需添加的一个条件是∠A=90°，理由如下：
∵AB∥DC，AD∥BC，
∴四边形ABCD是平行四边形，
又∵∠A=90°，
∴平行四边形ABCD是矩形，
故答案为：∠A=90°（答案不唯一）．
【点睛】本题考查了矩形的判定、平行四边形的判定与性质等知识，熟练掌握矩形的判定和平行四边形的判定与性质是解题的关键．
变式6-3．(2023·湖南益阳·统考中考真题）如图，已知四边形是平行四边形，从①，②，③中选择一个作为条件，补充后使四边形成为菱形，则其选择是___（限填序号）．
答案:①
分析：根据菱形的判定、矩形的判定、平行四边形的性质即可得．
【详解】解：①时，平行四边形是菱形（有一组邻边相等的平行四边形是菱形）；
②时，平行四边形是矩形（对角线相等的平行四边形是矩形）；
③由平行四边形的性质可知，，则不能作为构成菱形的条件；
故答案为：①．
【点睛】本题考查了菱形的判定、矩形的判定、平行四边形的性质，熟练掌握菱形的判定方法是解题关键．
变式6-4．(2023·黑龙江·统考中考真题）如图，在平行四边形中，对角线、相交于点O，在不添加任何辅助线的情况下，请你添加一个条件______________，使平行四边形是矩形．．

答案:
分析：根据矩形的判定方法即可得出答案．
【详解】解：∵四边形ABCD为平行四边形，
∴当时，四边形ABCD为矩形．
故答案为：．
【点睛】本题考查了矩形的判定，熟记矩形的判定方法是解题的关键．
考查题型七 矩形的证明
典例7．(2023·湖北恩施·统考中考真题）如图，在四边形ABCD中，∠A=∠B=90°，AD=10cm，BC=8cm，点P从点D出发，以1cm/s的速度向点A运动，点M从点B同时出发，以相同的速度向点C运动，当其中一个动点到达端点时，两个动点同时停止运动．设点P的运动时间为t（单位：s），下列结论正确的是（ ）
A．当时，四边形ABMP为矩形
B．当时，四边形CDPM为平行四边形
C．当时，
D．当时，或6s
答案:D
分析：计算AP和BM的长，得到AP≠BM，判断选项A；计算PD和CM的长，得到PD≠CM，判断选项B；按PM=CD，且PM与CD不平行，或PM=CD，且PM∥CD分类讨论判断选项C和D．
【详解】解：由题意得PD=t，AP=AD-PD=10-t，BM=t，CM=8-t，∠A=∠B=90°，
A、当时，AP=10-t=6 cm，BM=4 cm，AP≠BM，则四边形ABMP不是矩形，该选项不符合题意；
B、当时，PD=5 cm，CM=8-5=3 cm，PD≠CM，则四边形CDPM不是平行四边形，该选项不符合题意；
作CE⊥AD于点E，则∠CEA=∠A=∠B=90°，
∴四边形ABCE是矩形，
∴BC=AE=8 cm，
∴DE=2 cm，
当PM=CD，且PM与CD不平行时，作MF⊥AD于点F，CE⊥AD于点E，
∴四边形CEFM是矩形，
∴FM=CE；
∴Rt△PFM≌Rt△DEC（HL），
∴PF=DE=2，EF=CM=8-t，
∴AP=10-4-(8-t)=10-t，
解得t=6 s；
当PM=CD，且PM∥CD时，
∴四边形CDPM是平行四边形，
∴DP=CM，
∴t=8-t，
解得t=4 s；
综上，当PM=CD时，t=4s或6s；选项C不符合题意；选项D符合题意；
故选：D．
【点睛】此题重点考查矩形的判定与性质、全等三角形的判定与性质，解题的关键是正确地作出解题所需要的辅助线，应注意分类讨论，求出所有符合条件的t的值．
变式7-1．(2023·江苏无锡·统考中考真题）如图，D、E、F分别是各边中点，则以下说法错误的是（ ）
A．和的面积相等
B．四边形是平行四边形
C．若，则四边形是菱形
D．若，则四边形是矩形
答案:C
分析：根据中位线的性质，相似三角形的判定和性质，平行四边形、菱形、矩形的判定定理逐一判断各个选项，即可得到答案．
【详解】解： ∵点D、E、F分别是△ABC三边的中点，
∴DE、DF为△ABC得中位线，
∴ED∥AC，且ED＝AC＝AF；同理DF∥AB，且DF＝AB＝AE，
∴四边形AEDF一定是平行四边形，故B正确；
∴，
∴， ，
∴和的面积相等，故A正确；
∵，
∴DF＝AB=AE，
∴四边形不一定是菱形，故C错误；
∵∠A＝90°，则四边形AEDF是矩形，故D正确；
故选：C．
【点睛】本题考查三角形中位线性质定理和平行四边形、矩形、菱形的判定定理，相似三角形的判定和性质，熟练掌握上述性质定理和判定定理是解题的关键．
变式7-2．(2023·四川遂宁·统考中考真题）如图，在菱形ABCD中，对角线AC、BD相交于点O，点E是AD的中点，连接OE，过点D作DF∥AC交OE的延长线于点F，连接AF．
(1)求证：≌；
(2)判定四边形AODF的形状并说明理由．
答案:(1)见解析
(2)四边形AODF为矩形，理由见解析
分析：（1）利用全等三角形的判定定理即可；
（2）先证明四边形AODF为平行四边形，再结合∠AOD=90°，即可得出结论．
【详解】（1）证明：∵E是AD的中点，
∴AE=DE，
∵DF∥AC，
∴∠OAD=∠ADF，
∵∠AEO=∠DEF，
∴△AOE≌△DFE（ASA）；
（2）解：四边形AODF为矩形．
理由：∵△AOE≌△DFE，
∴AO=DF，
∵DF∥AC，
∴四边形AODF为平行四边形，
∵四边形ABCD为菱形，
∴AC⊥BD，
即∠AOD=90°，
∴平行四边形AODF为矩形．
【点睛】本题考查菱形的性质、全等三角形的判定与性质、矩形的判定，熟练掌握全等三角形的判定与性质以及矩形的判定是解题的关键．
变式7-3．(2023·湖北十堰·统考中考真题）如图，中，，相交于点，，分别是，的中点．
(1)求证：；
(2)设，当为何值时，四边形是矩形？请说明理由．
答案:(1)证明见解析
(2)当时，四边形是矩形，理由见解析
分析：（1）连接，先根据平行四边形的性质可得，再根据线段中点的定义可得，然后根据平行四边形的判定可得四边形是平行四边形，最后根据平行四边形的性质即可得证；
（2）先根据矩形的判定可得当时，四边形是矩形，再根据线段中点的定义、平行四边形的性质可得，由此即可得出的值．
【详解】（1）证明：如图，连接，
四边形是平行四边形，
，
分别是，的中点，
，
四边形是平行四边形，
．
（2）解：由（1）已证：四边形是平行四边形，
要使平行四边形是矩形，则，
，
，即，
，
故当时，四边形是矩形．
【点睛】本题考查了平行四边形的判定与性质、矩形的判定等知识点，熟练掌握平行四边形的判定与性质是解题关键．
变式7-4．(2023·上海·统考中考真题）已知：在圆O内，弦与弦交于点分别是和的中点，联结．
（1）求证：；
（2）联结，当时，求证：四边形为矩形．
答案:（1）见解析；（2）见解析
分析：（1）连结，由M、N分别是和的中点，可得OM⊥BC，ON⊥AD，由， 可得，可证，，根据等腰三角形三线合一性质;
（2）设OG交MN于E，由，可得，可得，，可证可得，由CN∥OG，可得，由可得AM∥CN，可证是平行四边形，再由可证四边形ACNM是矩形．
【详解】证明：（1）连结，
∵M、N分别是和的中点，
∴OM，ON为弦心距，
∴OM⊥BC，ON⊥AD，
，
在中，，
，
在Rt△OMG和Rt△ONG中，
，
，
∴，
;

（2）设OG交MN于E，
，
∴，
∴，即，
，
在△CMN和△ANM中
，
，
，
∵CN∥OG，
，
，
，
∴AM∥CN，
是平行四边形，
，
∴四边形ACNM是矩形．
【点睛】本题考查垂径定理，三角形全等判定与性质，等腰三角形判定与性质，平行线判定与性质，矩形的判定，掌握垂径定理，三角形全等判定与性质，等腰三角形判定与性质，平行线判定与性质，矩形的判定是解题关键．
考查题型八 矩形性质与判定综合
典例8．(2023·海南·统考中考真题）如图，菱形中，点E是边的中点，垂直交的延长线于点F，若，则菱形的边长是（ ）
A．3B．4C．5D．
答案:B
分析：过C作CM⊥AB延长线于M，根据设，由菱形的性质表示出BC=4x，BM=3x，根据勾股定理列方程计算即可．
【详解】过C作CM⊥AB延长线于M，
∵
∴设
∵点E是边的中点
∴
∵菱形
∴，CE∥AB
∵⊥，CM⊥AB
∴四边形EFMC是矩形
∴，
∴BM=3x
在Rt△BCM中，
∴，解得或（舍去）
∴
故选：B．
【点睛】本题考查了菱形的性质、矩形的判定与性质、勾股定理，关键在于熟悉各个知识点在本题的灵活运用．属于拔高题．
变式8-1．(2023·湖南湘西·统考中考真题）如图，在Rt△ABC中，∠A＝90°，M为BC的中点，H为AB上一点，过点C作CG∥AB，交HM的延长线于点G，若AC＝8，AB＝6，则四边形ACGH周长的最小值是（ ）
A．24B．22C．20D．18
答案:B
分析：通过证明△BMH≌△CMG可得BH＝CG，可得四边形ACGH的周长即为AB+AC+GH，进而可确定当MH⊥AB时，四边形ACGH的周长有最小值，通过证明四边形ACGH为矩形可得HG的长，进而可求解．
【详解】∵CG∥AB，
∴∠B＝∠MCG，
∵M是BC的中点，
∴BM＝CM，
在△BMH和△CMG中，
，
∴△BMH≌△CMG（ASA），
∴HM＝GM，BH＝CG，
∵AB＝6，AC＝8，
∴四边形ACGH的周长＝AC+CG+AH+GH＝AB+AC+GH＝14+GH，
∴当GH最小时，即MH⊥AB时四边形ACGH的周长有最小值，
∵∠A＝90°，MH⊥AB，
∴GH∥AC，
∴四边形ACGH为矩形，
∴GH＝8，
∴四边形ACGH的周长最小值为14+8＝22，
故选：B．
【点睛】本题主要考查全等三角形的判定与性质，确定GH的值是解题的关键．
变式8-2．(2023·四川乐山·统考中考真题）如图，等腰△ABC的面积为2，AB=AC，BC=2．作AE∥BC且AE=BC．点P是线段AB上一动点，连接PE，过点E作PE的垂线交BC的延长线于点F，M是线段EF的中点．那么，当点P从A点运动到B点时，点M的运动路径长为（ ）
A．B．3C．D．4
答案:B
分析：当P与A重合时，点F与C重合，此时点M在N处，当点P与B重合时，如图，点M的运动轨迹是线段MN．求出CF的长即可解决问题．
【详解】解：过点A作AD⊥BC于点D，连接CE，
∵AB=AC，
∴BD=DC=BC=1，
∵AE=BC，
∴AE=DC=1，
∵AE∥BC，
∴四边形AECD是矩形，
∴S△ABC=BC×AD=×2×AD=2，
∴AD=2，则CE=AD=2，
当P与A重合时，点F与C重合，此时点M在CE的中点N处，
当点P与B重合时，如图，点M的运动轨迹是线段MN．
∵BC=2，CE=2，
由勾股定理得BE=4，
cs∠EBC=，即，
∴BF=8，
∴CF=BF-BC=6,
∵点N是CE的中点，点M是EF的中点，
∴MN=CF=3，
∴点M的运动路径长为3，
故选：B．
【点睛】本题考查点的轨迹、矩形的判定和性质、解直角三角形、勾股定理等知识，解题的关键是正确寻找点M的运动轨迹，学会利用起始位置和终止位置寻找轨迹，属于中考填空题中的压轴题．
变式8-3．(2023·四川自贡·统考中考真题）如图，矩形中，，是的中点，线段在边上左右滑动；若，则的最小值为____________．
答案:
分析：如图，作G关于AB的对称点G'，在CD上截取CH=1，然后连接HG'交AB于E，在EB上截取EF=1，此时GE+CF的值最小，可得四边形EFCH是平行四边形，从而得到G'H=EG'+EH=EG+CF，再由勾股定理求出HG'的长，即可求解．
【详解】解：如图，作G关于AB的对称点G'，在CD上截取CH=1，然后连接HG'交AB于E，在EB上截取EF=1，此时GE+CF的值最小，

∴G'E=GE，AG=AG'，
∵四边形ABCD是矩形，
∴AB∥CD，AD=BC=2
∴CH∥EF，
∵CH=EF=1，
∴四边形EFCH是平行四边形，
∴EH=CF，
∴G'H=EG'+EH=EG+CF，
∵AB=4，BC=AD=2，G为边AD的中点，
∴AG=AG'=1
∴DG′=AD+AG'=2+1=3，DH=4-1=3，
∴，
即的最小值为．
故答案为：
【点睛】此题主要考查了利用轴对称求最短路径问题，矩形的性质，勾股定理等知识，确定GE+CF最小时E，F位置是解题关键．
变式8-4．(2023·湖南娄底·统考中考真题）九年级融融陪同父母选购家装木地板，她感觉某品牌木地板拼接图（如实物图）比较美观，通过手绘（如图）、测量、计算发现点是的黄金分割点，即．延长与相交于点，则________.（精确到0.001）

答案:0.618
分析：设每个矩形的长为x，宽为y，则DE＝AD－AE＝x－y，四边形EFGM是矩形，则EG＝MF＝y，由得x－y≈0.618x，求得y≈0.382x，进一步求得，即可得到答案．
【详解】解：如图，设每个矩形的长为x，宽为y，则DE＝AD－AE＝x－y，
由题意易得∠GEM＝∠EMF＝∠MFG＝90°，
∴四边形EFGM是矩形，
∴EG＝MF＝y，
∵，
∴x－y≈0.618x，
解得y≈0.382x，
∴，
∴EG≈0.618DE．
故答案为：0.618．
【点睛】此题考查了矩形的判定和性质、分式的化简、等式的基本性质、二元一次方程等知识，求得y≈0.382x是解题的关键．