2024中考数学全国真题分类卷 第二十四讲 图形的对称、平移、旋转与位似 强化训练(含答案)

这是一份2024中考数学全国真题分类卷 第二十四讲 图形的对称、平移、旋转与位似 强化训练(含答案)，共23页。试卷主要包含了 题目等内容，欢迎下载使用。
命题点1 轴对称图形与中心对称图形
1. (2023邵阳)下列四种图形中，对称轴条数最多的是( )
A. 等边三角形 B. 圆 C. 长方形 D. 正方形
2. (2023北京)图中的图形为轴对称图形，该图形的对称轴的条数为( )
第2题图
A. 1 B. 2 C. 3 D. 5
3. (2023山西)2023年4月16日，神舟十三号载人飞船圆满完成全部既定任务，顺利返回地球家园．六个月的飞天之旅展现了中国航天科技的新高度．下列航天图标，其文字上方的图案是中心对称图形的是( )
4. (2023福建)美术老师布置同学们设计窗花，下列作品为轴对称图形的是( )
5. (新趋势)·数学文化 (2023遂宁)下面图形中既是轴对称图形又是中心对称图形的是( )
A. 科克曲线 B. 笛卡尔心形线
C. 阿基米德螺旋线 D. 赵爽弦图
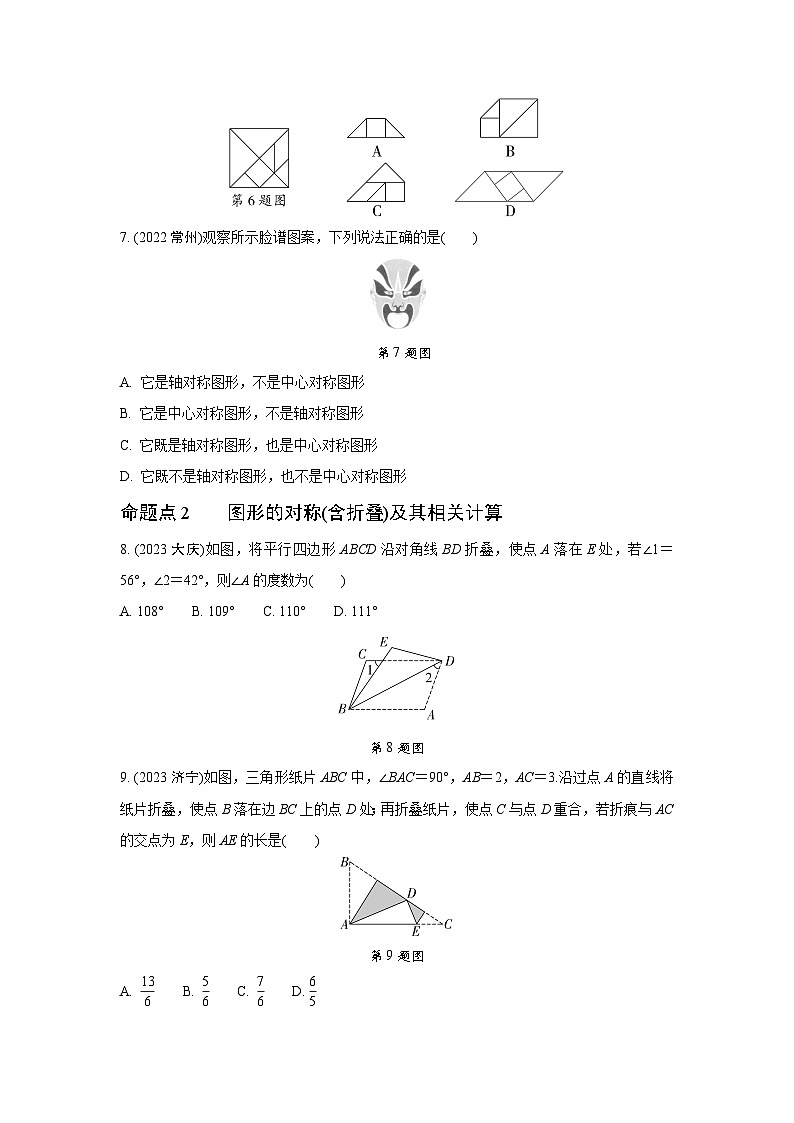
6. (2022枣庄)将如图的七巧板的其中几块，拼成一个多边形，为中心对称图形的是( )
7. (2022常州)观察所示脸谱图案，下列说法正确的是( )
第7题图
A. 它是轴对称图形，不是中心对称图形
B. 它是中心对称图形，不是轴对称图形
C. 它既是轴对称图形，也是中心对称图形
D. 它既不是轴对称图形，也不是中心对称图形
命题点2 图形的对称(含折叠)及其相关计算
8. (2023大庆)如图，将平行四边形ABCD沿对角线BD折叠，使点A落在E处，若∠1＝56°，∠2＝42°，则∠A的度数为( )
A. 108° B. 109° C. 110° D. 111°
第8题图
9. (2023济宁)如图，三角形纸片ABC中，∠BAC＝90°，AB＝2，AC＝3.沿过点A的直线将纸片折叠，使点B落在边BC上的点D处；再折叠纸片，使点C与点D重合，若折痕与AC的交点为E，则AE的长是( )
第9题图
A. eq \f(13,6) B. eq \f(5,6) C. eq \f(7,6) D. eq \f(6,5)
10. (2023河北)题目：“如图，∠B＝45°，BC＝2，在射线BM上取一点A，设AC＝d，若对于d的一个数值，只能作出唯一一个△ABC，求d的取值范围．”对于其答案，甲答：d≥2，乙答：d＝1.6，丙答：d＝ eq \r(2) ，则正确的是( )
A. 只有甲答的对 B. 甲、丙答案合在一起才完整
C. 甲、乙答案合在一起才完整 D. 三人答案合在一起才完整
第10题图
11. (2023金华)如图是一张矩形纸片ABCD，点E为AD中点，点F在BC上，把该纸片沿EF折叠，点A，B的对应点分别为A′，B′，A′E与BC相交于点G，B′A′的延长线过点C.若 eq \f(BF,GC) ＝ eq \f(2,3) ，则 eq \f(AD,AB) 的值为( )
第11题图
A. 2 eq \r(2) B. eq \f(4\r(10),5) C. eq \f(20,7) D. eq \f(8,3)
12. (2023连云港)如图，将矩形ABCD沿着GE，EC，GF翻折，使得点A，B，D恰好都落在点O处，且点G，O，C在同一条直线上，同时点E，O，F在另一条直线上．小炜同学得出以下结论：
①GF∥EC；②AB＝ eq \f(4\r(3),5) AD；③GE＝ eq \r(6) DF；④OC＝2 eq \r(2) OF；⑤△COF∽△CEG.其中正确的是( )
第12题图
A. ①②③ B. ①③④
C. ①④⑤ D. ②③④
13. (2023潍坊)小莹按照如图所示的步骤折叠A4纸，折完后，发现折痕AB′与A4纸的长边AB恰好重合，那么A4纸的长AB与宽AD的比值为________．
第13题图
14. (2023雅安)如图，把一张矩形纸片沿对角线折叠，若BC＝9，CD＝3，那么阴影部分的面积为________．
第14题图
15. (2020安徽)在数学探究活动中，敏敏进行了如下操作：如图，将四边形纸片ABCD沿过点A的直线折叠，使得点B落在CD上的点Q处．折痕为AP；再将△PCQ，△ADQ分别沿PQ，AQ折叠，此时点C，D落在AP上的同一点R处．请完成下列探究：
(1)∠PAQ的大小为________°；
(2)当四边形APCD是平行四边形时， eq \f(AB,QR) 的值为________．
第15题图
16. (2023台州)如图，在菱形ABCD中，∠A＝60°，AB＝6.折叠该菱形，使点A落在边BC上的点M处，折痕分别与边AB，AD交于点E，F.当点M与点B重合时，EF的长为________；当点M的位置变化时，DF长的最大值为________．
第16题图
17. (2023无锡)如图，已知四边形ABCD为矩形，AB＝2 eq \r(2) ，BC＝4，点E在BC上，CE＝AE，将△ABC沿AC翻折到△AFC，连接EF.
(1)求EF的长；
(2)求sin ∠CEF的值．
第17题图
18. (2023绍兴)如图，在△ABC中，∠ABC＝40°，∠ACB＝90°，AE平分∠BAC交BC于点E.P是边BC上的动点(不与B，C重合)，连接AP，将△APC沿AP翻折得△APD，连接DC，记∠BCD＝α.
(1)如图，当P与E重合时，求α的度数；
(2)当P与E不重合时，记∠BAD＝β，探究α与β的数量关系．
命题点3 图形的平移及其相关计算
19. (2023广西北部湾经济区)2023北京冬残奥会的会徽是以汉字“飞”为灵感来设计的，展现了运动员不断飞跃，超越自我，奋力拼搏，激励世界的冬残奥精神．下列的四个图中，能由如图所示的会徽经过平移得到的是( )
20. (2023嘉兴)“方胜”是中国古代妇女的一种发饰，其图案由两个全等正方形相叠组成，寓意是同心吉祥．如图，将边长为2 cm的正方形ABCD沿对角线BD方向平移1 cm得到正方形A′B′C′D′，形成一个“方胜”图案，则点D，B′之间的距离为( )
A. 1 cm B. 2 cm C. ( eq \r(2) －1)cm D. (2 eq \r(2) －1)cm
第20题图
21. (2023福建)如图，现有一把直尺和一块三角尺，其中∠ABC＝90°，∠CAB＝60°，AB＝8，点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移，使得△ABC移动到△A′B′C′，点A′对应直尺的刻度为0，则四边形ACC′A′的面积是( )
第21题图
A. 96 B. 96 eq \r(3) C. 192 D. 160 eq \r(3)
22. (2023海南)如图，点A(0，3)，B(1，0)，将线段AB平移得到线段DC，若∠ABC＝90°，BC＝2AB，则点D的坐标是( )
A. (7，2) B. (7，5) C. (5，6) D. (6，5)
第22题图
23. (2023金华)如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝2 cm.把△ABC沿AB方向平移1 cm，得到△A′B′C′，连接CC′，则四边形AB′C′C的周长为________cm.
第23题图
24. (2023益阳)如图，将边长为3的正方形ABCD沿其对角线AC平移，使A的对应点A′满足AA′＝ eq \f(1,3) AC，则所得正方形与原正方形重叠部分的面积是________．
第24题图
命题点4 图形的旋转及其相关计算
25. (2022苏州)如图，在方格纸中，将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B，则下列四个图形中正确的是( )
26. (2023南充)如图，将直角三角板ABC绕顶点A顺时针旋转到△AB′C′，点B′恰好落在CA的延长线上，∠B＝30°，∠C＝90°，则∠BAC′为( )
A. 90° B. 60° C. 45° D. 30°
第26题图
27. (2023包头)如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝2，将△ABC绕点C顺时针旋转得到△A′B′C，其中点A′与点A是对应点，点B′与点B是对应点．若点B′恰好落在AB边上，则点A到直线A′C的距离等于( )
第27题图
A. 3 eq \r(3) B. 2 eq \r(3) C. 3 D. 2
28. (2023天津)如图，在△ABC中，AB＝AC，若M是BC边上任意一点，将△ABM绕点A逆时针旋转得到△ACN，点M的对应点为点N，连接MN，则下列结论一定正确的是( )
A. AB＝AN B. AB∥NC C. ∠AMN＝∠ACN D. MN⊥AC
源自人教八上P33第5题
第28题图
29. (2023苏州)如图，点A的坐标为(0，2)，点B是x轴正半轴上的一点，将线段AB绕点A按逆时针方向旋转60°得到线段AC，若点C的坐标为(m，3)，则m的值为( )
第29题图
A. eq \f(4\r(3),3) B. eq \f(2\r(21),3) C. eq \f(5\r(3),3) D. eq \f(4\r(21),3)
30. (2023贺州)如图，在平面直角坐标系中，△OAB为等腰三角形，OA＝AB＝5，点B到x轴的距离为4.若将△OAB绕点O逆时针旋转90°，得到△OA′B′，则点B′的坐标为________．
第30题图
31. (2023娄底)如图，已知等腰△ABC的顶角∠BAC的大小为θ，点D为边BC上的动点(与B，C不重合)，将AD绕点A沿顺时针方向旋转θ角度时点D落在D′处，连接BD′.给出下列结论：
①△ACD≌△ABD′；
②△ACB∽△ADD′；
③当BD＝CD时，△ADD′的面积取得最小值．
其中正确的结论有________(填结论对应的序号).
第31题图
32. (2023柳州)如图，在正方形ABCD中，AB＝4，G是BC的中点，点E是正方形内一个动点，且EG＝2，连接DE，将线段DE绕点D逆时针旋转90°得到线段DF，连接CF，则线段CF长的最小值为________．
第32题图
33. (2023随州)如图①，在矩形ABCD中，AB＝8，AD＝6，E，F分别为AB，AD的中点，连接EF.如图②，将△AEF绕点A逆时针旋转角θ(0°＜θ＜90°)，使EF⊥AD，连接BE并延长交DF于点H.则∠BHD的度数为________，DH的长为________.
第33题图
34. (2022绵阳)如图，点M是∠ABC的边BA上的动点，BC＝6，连接MC，并将线段MC绕点M逆时针旋转90°得到线段MN.
(1)作MH⊥BC，垂足H在线段BC上，当∠CMH＝∠B时，判断点N是否在直线AB上，并说明理由；
(2)若∠ABC＝30°，NC∥AB，求以MC、MN为邻边的正方形的面积S.
第34题图
35. (2023山西)综合与实践
问题情境：在Rt△ABC中，∠BAC＝90°，AB＝6，AC＝8.直角三角板EDF中∠EDF＝90°，将三角板的直角顶点D放在Rt△ABC斜边BC的中点处，并将三角板绕点D旋转，三角板的两边DE，DF分别与边AB，AC交于点M，N.
猜想证明：
(1)如图①，在三角板旋转过程中，当点M为边AB的中点时，试判断四边形AMDN的形状，并说明理由；
问题解决：
(2)如图②，在三角板旋转过程中，当∠B＝∠MDB时，求线段CN的长；
(3)如图③，在三角板旋转过程中，当AM＝AN时，直接写出线段AN的长．
第35题图
命题点5 图形的位似及其相关计算
36. (2023梧州)如图，以点O为位似中心，作四边形ABCD的位似图形A′B′C′D′，已知 eq \f(OA,OA′) ＝ eq \f(1,3) ，若四边形ABCD的面积是2，则四边形A′B′C′D′的面积是( )
A. 4 B. 6 C. 16 D. 18
第36题图
37. (2023成都)如图，△ABC和△DEF是以点O为位似中心的位似图形．若OA∶AD＝2∶3，则△ABC与△DEF的周长比是________．
第37题图
命题点6 网格作图及其相关计算
38. (2023陕西)如图，△ABC的顶点坐标分别为A(－2，3)，B(－3，0)，C(－1，－1).将△ABC平移后得到△A′B′C′，且点A的对应点是A′(2，3)，点B、C的对应点分别是B′、C′.
(1)点A、A′之间的距离是________；
(2)请在图中画出△A′B′C′.
第38题图
39. (2023湘潭)如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A(－1，1)，B(－4，0)，C(－2，2).将△ABC绕原点O顺时针旋转90°后得到△A1B1C1.
(1)请写出A1、B1、C1三点的坐标：A1______，B1______，C1______；
(2)求点B旋转到点B1的弧长．
第39题图
40. (2023河池)如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A(4，1)，B(2，3)，C(1，2).
(1)画出与△ABC关于y轴对称的△A1B1C1；
(2)以原点O为位似中心，在第三象限内画一个△A2B2C2，使它与△ABC的相似比为2∶1，并写出点B2的坐标．
第40题图
参考答案与解析
1. B 2. D 3. B 4. A 5. A 6. D 7. A
8. C 【解析】由题意得，2∠ABD＝∠1＝56°，∴∠ABD＝28°，∴∠A＝180°－∠ABD－∠2＝180°－28°－42°＝110°.
9. A 【解析】∵在三角形纸片ABC中，∠BAC＝90°，∴∠B＋∠C＝90°，由折叠的性质，得∠ADB＝∠B，∠CDE＝∠C，AD＝AB，DE＝CE，∴∠ADE＝180°－(∠ADB＋∠CDE)＝90°.设AE＝x，则CE＝DE＝3－x，在Rt△ADE中，AD＝AB＝2，根据勾股定理，得AD2＋DE2＝AE2，即22＋(3－x)2＝x2，解得x＝ eq \f(13,6) ，∴AE＝ eq \f(13,6) .
10. B 【解析】如解图，过点C作CD⊥BM于点D，如解图①，当点A与点D重合时，∵∠B＝45°，∠BAC＝90°，BC＝2，∴AC＝ eq \r(2) ，当d＝ eq \r(2) 时，△ABC为唯一三角形；如解图②，当点A在线段BD上，点A关于线段CD的对称点A′在射线DM上，∴当d＝1.6时，存在△ABC和△A′BC两个三角形；如解图③，当点A运动至AC⊥BC时，点A关于CD的对称点A′与点B重合，∵∠B＝45°，∠BCA＝90°，BC＝2，∴∠BAC＝45°，∴AC＝BC＝2，当d＝2时，△ABC为唯一三角形；当点A向M运动时，点A′不在射线BM上，即d>2时△ABC为唯一三角形，综上所述，当d＝ eq \r(2) 或d≥2时，△ABC为唯一三角形，故甲、丙答案合在一起才完整．
第10题解图
11. A 【解析】如解图，连接BE，B′E，CE，∵点E为AD的中点，∴根据矩形的轴对称性可知BE＝CE，由折叠可知BE＝B′E，∴B′E＝CE.∵EA′⊥B′C，∴点A′为B′C的中点，A′C＝A′B′＝AB＝ eq \f(1,2) B′C.∵A′G∥B′F，∴G为CF的中点．由折叠可知BF＝B′F，∵ eq \f(BF,GC) ＝ eq \f(2,3) ，∴ eq \f(BF,FC) ＝ eq \f(2,6) ＝ eq \f(1,3) .设A′G＝x，则B′F＝BF＝2x，CG＝FG＝3x，AD＝BC＝8x，在Rt△CB′F中，B′C＝ eq \r(CF2－B′F2) ＝ eq \r(（6x）2－（2x）2) ＝4 eq \r(2) x，∴AB＝2 eq \r(2) x，∴ eq \f(AD,AB) ＝ eq \f(8x,2\r(2)x) ＝2 eq \r(2) .
第11题解图
12. B 【解析】由折叠的性质得，∠GEO＝∠GEA，∠OEC＝∠BEC，∴∠GEC＝∠GEO＋∠CEO＝90°，同理可得，∠FGE＝90°，∴∠FGE＋∠GEC＝180°，∴GF∥EC，①正确；∵OE＝EA＝EB，GO＝DG＝GA，∴点E，G分别为AB，AD的中点，设AB＝2a，AD＝2b，则OE＝EA＝EB＝a，GO＝DG＝GA＝b，∵OC＝BC＝2b，∴GC＝GO＋OC＝3b，在Rt△GDC中，DC2＋DG2＝GC2，即(2a)2＋b2＝(3b)2，∴a2＝2b2.∵a，b均大于0，∴a＝ eq \r(2) b，∴ eq \f(AB,AD) ＝ eq \f(2a,2b) ＝ eq \r(2) ，即AB＝ eq \r(2) AD，②错误；∵∠FGE＝90°，∴∠FGD＋∠AGE＝90°.∵∠AGE＋∠GEA＝180°－∠A＝90°，∴∠DGF＝∠AEG.∵∠D＝∠A＝90°，∴△DGF∽△AEG，∴ eq \f(DF,AG) ＝ eq \f(DG,AE) ＝ eq \f(b,a) ＝ eq \f(\r(2),2) ，∴DF＝ eq \f(\r(2),2) b.∵GE＝ eq \r(AG2＋AE2) ＝ eq \r(b2＋a2) ＝ eq \r(b2＋（\r(2)b）2) ＝ eq \r(3) b，∴GE＝ eq \r(6) DF，③正确；∵OF＝DF＝ eq \f(\r(2),2) b，OC＝2b，∴OC＝2 eq \r(2) OF，④正确；∵CE＝ eq \r(BC2＋EB2) ＝ eq \r(（2b）2＋a2) ＝ eq \r(（2b）2＋（\r(2)b）2) ＝ eq \r(6) b，∴ eq \f(CE,GE) ＝ eq \f(\r(6)b,\r(3)b) ＝ eq \r(2) ，∵ eq \f(OC,OF) ＝2 eq \r(2) ，∴ eq \f(OC,OF) ≠ eq \f(CE,GE) ，∴△COF与△CEG不相似，⑤错误．综上所述，正确的是①③④.
13. eq \r(2) 【解析】由第②次折叠知，AB＝AB′，设AD′＝AD＝x，由第①次折叠知，∠B′AB＝45°，∴△AD′B′是等腰直角三角形，∴AB′＝ eq \r(2) AD′，∴长AB与宽AD的比值为 eq \r(2) .
14. eq \f(15,2) 【解析】由折叠的性质可得，BC＝BE，∠DBC＝∠DBF，∵四边形ABCD是矩形，∴AD∥BC，∠E＝∠C＝90°，∴∠FDB＝∠DBC，∴∠FDB＝∠DBF，∴FD＝FB，设FD＝FB＝x，则FE＝BE－BF＝9－x，在Rt△FED中，由勾股定理得，FD2＝FE2＋ED2，即x2＝(9－x)2＋32，解得x＝5，∴FD＝5，∴S阴影＝ eq \f(1,2) FD·AB＝ eq \f(1,2) ×5×3＝ eq \f(15,2) .
15. (1)30；(2) eq \r(3) 【解析】(1)由折叠的性质得，∠B＝∠AQP，∠DAQ＝∠QAP＝∠PAB，∠DQA＝∠AQR，∠CQP＝∠PQR，∠D＝∠ARQ，∠C＝∠QRP，∵∠QRA＋∠QRP＝180°，∴∠D＋∠C＝180°，∴AD∥BC，∴∠B＋∠DAB＝180°，∵∠DQR＋∠CQR＝180°，∴∠DQA＋∠CQP＝90°，∴∠AQP＝90°，∴∠B＝∠AQP＝90°，∴∠DAB＝90°，∴∠DAQ＝∠QAP＝∠PAB＝30°；(2)由折叠的性质可得，AD＝AR，CP＝PR，∵四边形APCD是平行四边形，∴AD＝PC，∴AR＝PR，又∵∠AQP＝90°，∴QR＝ eq \f(1,2) AP，∵∠PAB＝30°，∠B＝90°，∴AP＝2PB，AB＝ eq \r(3) PB，∴PB＝QR，∴ eq \f(AB,QR) ＝ eq \r(3) .
16. 3 eq \r(3) ；6－3 eq \r(3) 【解析】如解图①，此时点M与点B重合，根据折叠的性质，对应点的连线垂直于折痕，可知DE⊥AB，∵∠A＝60°，AB＝6，∴EF＝AD·sin 60°＝6× eq \f(\r(3),2) ＝3 eq \r(3) ；如解图②，过点D作DH⊥BC于点H，∵DF＝AD－AF，∴当AF长最小时，DF长最大，根据折叠的性质，AF＝MF，∴当MF的长最短时，DF长最大，而MF⊥BC时最短，∵四边形ABCD为菱形，∴DH＝FM，∠C＝∠A＝60°，DC＝AB＝6，∴此时AF＝FM＝DH＝DC·sin 60°＝6× eq \f(\r(3),2) ＝3 eq \r(3) ，∴DF的最大值为AD－AF＝6－3 eq \r(3) .
第16题解图
17. 解：(1)设BE＝x，则CE＝BC－BE＝4－x，
∵CE＝AE，
∴∠ACE＝∠CAE，AE＝4－x，
∵四边形ABCD是矩形，
∴∠B＝90°，
在Rt△ABE中，有AE2＝BE2＋AB2，
∴(4－x)2＝x2＋(2 eq \r(2) )2，
解得x＝1，即BE＝1，
∴CE＝AE＝4－1＝3，
由折叠的性质可得，∠AFC＝∠B＝90°，∠ACE＝∠ACF，AB＝AF＝2 eq \r(2) ，
∴∠CAE＝∠ACF，
∴CF∥AE，
∴∠EAF＝90°，
∴EF＝ eq \r(AF2＋AE2) ＝ eq \r(（2\r(2)）2＋32) ＝ eq \r(17) ；
(2)如解图，过点C作CH⊥EF于点H，则∠CHF＝90°，
由(1)知CF∥AE，∠EAF＝90°，
第17题解图
∴∠CFH＝∠AEF，
∵∠EAF＝∠CHF＝90°，
∴△HFC∽△AEF，
∴ eq \f(CH,FA) ＝ eq \f(CF,FE) ，
由折叠的性质可得，CF＝BC＝4，AF＝AB＝2 eq \r(2) ，
∴ eq \f(CH,2\r(2)) ＝ eq \f(4,\r(17)) ，解得CH＝ eq \f(8\r(34),17) ，
∴sin ∠CEF＝ eq \f(CH,CE) ＝ eq \f(\f(8\r(34),17),3) ＝ eq \f(8\r(34),51) .
18. 解：(1)∵∠B＝40°，∠ACB＝90°，
∴∠BAC＝50°，
∵AE平分∠BAC，
∴∠EAC＝ eq \f(1,2) ∠BAC＝25°，
∵P与E重合，
∴D在AB边上，AE⊥CD，
∴∠ACD＝90°－25°＝65°，
∴α＝∠ACB－∠ACD＝25°；
(2)①如解图①，当点P在线段BE上时，
∵∠ADC＝∠ACD＝90°－α，∠ADC＋∠BAD＝∠B＋∠BCD，
∴90°－α＋β＝40°＋α，
∴2α－β＝50°；
②如解图②，当点P在线段CE上时，
延长AD交BC于点F，
∵∠ADC＝∠ACD＝90°－α，∠ADC＝∠AFC＋α＝∠ABC＋∠BAD＋α＝40°＋α＋β，
∴90°－α＝40°＋α＋β，
∴2α＋β＝50°.
综上所述，当点P在线段BE上时，2α－β＝50°；当点P在线段CE上时，2α＋β＝50°.
图①

图②
第18题解图
19. D
20. D 【解析】由题意得，BD＝2 eq \r(2) cm，由平移性质得BB′＝1 cm，∴点D，B′之间的距离为DB′＝BD－BB′＝(2 eq \r(2) －1)cm.
21. B 【解析】∵AB＝8，∠BAC＝60°，∴BC＝ eq \r(3) AB＝8 eq \r(3) ，由点A对应的刻度为12，点A′对应的刻度为0，可知平移距离AA′＝12，∴S四边形ACC′A′＝AA′·BC＝12×8 eq \r(3) ＝96 eq \r(3) .
22. D 【解析】由平移的性质可知，四边形ABCD是平行四边形，∵∠ABC＝90°，∴四边形ABCD是矩形，∴∠BAD＝90°，∵A(0，3)，B(1，0)，∴OA＝3，OB＝1，如解图，过点D作DE⊥y轴于点E，∴∠DEA＝∠AOB＝90°，∴∠OAB＋∠OBA＝90°，∵∠OAB＋∠EAD＝90°，∴∠EAD＝∠OBA，∴△EAD∽△OBA，∵BC＝2AB，∴ eq \f(EA,OB) ＝ eq \f(AD,BA) ＝ eq \f(ED,OA) ＝ eq \f(2,1) ，∴EA＝2，ED＝6，∴OE＝5，∴点D的坐标为(6，5).
第22题解图
23. 8＋2 eq \r(3) 【解析】在Rt△ABC中，∵∠ACB＝90°，∠A＝30°，BC＝2 cm，∴AB＝4 cm，AC＝2 eq \r(3) cm.∵把△ABC沿AB方向平移1 cm，得到△A′B′C′，∴四边形AB′C′C的周长为AB＋BB′＋B′C′＋C′C＋AC＝4＋1＋2＋1＋2 eq \r(3) ＝8＋2 eq \r(3) (cm).
24. 4 【解析】由题意可知重叠部分的图形为正方形，∵正方形的边长为3，∴AC＝3 eq \r(2) ，∵AA′＝ eq \f(1,3) AC，∴A′C＝ eq \f(2,3) AC＝2 eq \r(2) ，∴重叠部分正方形的边长为2，∴重叠部分正方形的面积为4.
25. B 【解析】A选项是原图形的对称图形，故A不正确；B选项是Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B，故B正确；C选项旋转后的形状发生了改变，故C不正确；D选项是按逆时针方向旋转90°，故D不正确．
26. B 【解析】∵∠C＝90°，∠B＝30°，∴∠BAC＝180°－∠B－∠C＝60°，由旋转的性质可知△ABC≌△AB′C′，∴∠BAC＝∠B′AC′＝60°，又∵C，A，B′三点共线，∴∠BAC′＝180°－∠BAC－∠B′AC′＝60°.
27. C 【解析】如解图，连接AA′，过点A作AD⊥A′C于点D，∵在Rt△ABC中，∠BAC＝30°，BC＝2，∴AC＝ eq \f(BC,tan 30°) ＝2 eq \r(3) ，∠B＝60°，由旋转的性质得，BC＝B′C，AC＝AC′，∴△BCB′为等边三角形，∴∠BCB′＝∠ACA′＝60°，∴△ACA′为等边三角形，∴∠CAD＝30°，∴AD＝AC·cs 30°＝2 eq \r(3) × eq \f(\r(3),2) ＝3.
第27题解图
28. C 【解析】∵△ACN是由△ABM绕点A逆时针旋转得到的，∴△ACN≌△ABM，∴AN＝AM，∵AM与AB不一定相等，∴AB与AN不一定相等，故选项A不一定正确；AB，NC平行的理由不充分，故选项B不一定正确；∵△ABM≌△ACN，∴∠BAM＝∠CAN，∠ABM＝∠ACN，∴∠BAM＋∠MAC＝∠CAN＋∠MAC，即∠BAC＝∠MAN，∵AM＝AN，∴∠AMN＝∠ANM＝ eq \f(180°－∠MAN,2) ，∵AB＝AC，∴∠ABC＝∠ACB＝ eq \f(180°－∠BAC,2) ，∴∠AMN＝∠ABC，∴∠AMN＝∠ACN，故选项C一定正确；MN，AC垂直的理由不充分，故选项D不一定正确．
29. C 【解析】如解图，连接BC，过点C作AB，x轴的垂线，垂足分别为D，E，过点D作x轴的平行线，分别交y轴，CE于点M，N，则四边形MOEN为矩形．∵AC由AB绕点A逆时针旋转60°得到，∴AC＝AB，∠BAC＝60°，∴△ABC为等边三角形，∴点D为AB的中点， eq \f(CD,AD) ＝tan 60°＝ eq \r(3) ，∴点M为AO的中点，∵A(0，2)，∴AM＝MO＝NE＝1，∵C(m，3)，∴CN＝CE－NE＝2，∵∠ADC＝90°，∴∠CDN＋∠ADM＝90°，∵∠DAM＋∠ADM＝90°，∴∠CDN＝∠DAM，∴△CDN∽△DAM，∴ eq \f(CN,DM) ＝ eq \f(DN,AM) ＝ eq \f(CD,DA) ，即 eq \f(2,DM) ＝ eq \f(DN,1) ＝ eq \r(3) ，∴DM＝ eq \f(2\r(3),3) ，DN＝ eq \r(3) ，∴MN＝DM＋DN＝ eq \f(5\r(3),3) ，即m的值为 eq \f(5\r(3),3) .
第29题解图
30. (－4，8) 【解析】如解图，过点B作BC⊥x轴，BD⊥y轴，过点B′作B′C′⊥y轴，B′D′⊥x轴，∵AB＝5，BC＝4，∴CA＝3，∴A′C′＝3，又∵B′C′＝BC＝4，∴D′O＝B′C′＝4，B′D′＝OC′＝5＋3＝8，∴点B′的坐标为(－4，8).
第30题解图
31. ①②③ 【解析】由旋转性质可得∠BAC＝∠DAD′＝θ，AD＝AD′，∴∠BAC－∠DAB＝∠DAD′－∠DAB，即∠CAD＝∠BAD′，∵AC＝AB，∴△ACD≌△ABD′，故①正确；∵AC＝AB，AD＝AD′，∴ eq \f(AC,AB) ＝ eq \f(AD,AD′) ＝1，∵∠BAC＝∠DAD′，∴△ACB∽△ADD′，故②正确；如解图，过点D作DH⊥AD′于点H，则∠AHD＝90°，∴sin θ＝ eq \f(DH,AD) ，∴DH＝AD·sin θ，∴S△ADD′＝ eq \f(1,2) AD′·DH＝ eq \f(1,2) AD2·sin θ，∴当AD取得最小值时，即AD⊥BC时，△ADD′的面积最小．∵AB＝AC，∴当BD＝DC时，△ADD′的面积最小，故③正确．综上所述，正确的结论是①②③.
第31题解图
32. 2 eq \r(5) －2 【解析】如解图，连接AE，AG，∵线段DE绕点D逆时针旋转90°得到线段DF，∴∠EDF＝90°，DE＝DF，∵∠ADC＝90°，∴∠ADE＝∠CDF，∵AD＝CD，∴△ADE≌△CDF，∴AE＝CF，AE＋EG≥AG，∴AE≥AG－EG，∵AG＝ eq \r(AB2＋BG2) ＝ eq \r(42＋22) ＝2 eq \r(5) ，EG＝2，∴AE≥2 eq \r(5) －2，∴CF长的最小值为2 eq \r(5) －2.
第32题解图
33. 90°， eq \f(4\r(5),5) 【解析】如解图，设AD分别交BH，EF于点M，N，∵四边形ABCD为矩形，∴∠ABC＝∠BAD＝90°，∵E，F分别为AB，AD的中点，∴AE＝ eq \f(1,2) AB＝4，AF＝ eq \f(1,2) AD＝3，∴ eq \f(AE,AF) ＝ eq \f(AB,AD) ＝ eq \f(4,3) ，由旋转的性质得∠BAE＝∠DAF，∴△ABE∽△ADF，∴∠ABE＝∠ADF，∵∠ABM＋∠AMB＝90°，∠AMB＝∠DMH，∴∠ADF＋∠DMH＝90°，∴∠BHD＝90°.在Rt△AEF中，EF＝ eq \r(AF2＋AE2) ＝5，S△AEF＝ eq \f(1,2) AF·AE＝ eq \f(1,2) EF·AN，解得AN＝ eq \f(12,5) ，∴DN＝AD－AN＝ eq \f(18,5) ，tan ∠AFE＝ eq \f(AN,NF) ＝ eq \f(AE,AF) ＝ eq \f(4,3) ，解得NF＝ eq \f(9,5) ，∴DF＝ eq \r(DN2＋FN2) ＝ eq \f(9\r(5),5) ，∴cs ∠DFN＝ eq \f(FN,DF) ＝ eq \f(FH,EF) ，解得FH＝ eq \r(5) ，∴DH＝DF－FH＝ eq \f(4\r(5),5) .
第33题解图
34. 解：(1)点N在直线AB上．
理由：∵MH⊥BC，
∴∠B＋∠BMH＝90°，
∵∠B＝∠CMH，
∴∠BMC＝∠CMH＋∠BMH＝90°.
∴CM⊥AB.
∴将线段MC绕点M逆时针旋转90°得到线段MN，点N在直线AB上；
(2)如解图，过点C作CD⊥AB于点D，
∵∠B＝30°，BC＝6，
∴CD＝ eq \f(1,2) BC＝3，
∵CM＝MN，CM⊥MN，
第34题解图
∴△CMN是等腰直角三角形，∠MCN＝45°.
∵NC∥AB，
∴∠DMC＝∠MCN＝45°，
∴△CDM是等腰直角三角形，
∴CM＝ eq \r(2) CD＝3 eq \r(2) ，
∴S＝CM2＝(3 eq \r(2) )2＝18.
35. 解：(1)四边形AMDN为矩形．
理由：∵点M为AB的中点，点D为BC的中点，
∴MD∥AC，
∴∠AMD＋∠A＝180°.
∵∠A＝90°，
∴∠AMD＝90°.
∵∠EDF＝90°，
∴∠A＝∠AMD＝∠MDN＝90°，
∴四边形AMDN为矩形；
(2)如解图①，过点N作NG⊥BC于点G，∵在Rt△ABC中，∠A＝90°，AB＝6，AC＝8，
∴∠B＋∠C＝90°，BC＝ eq \r(AB2＋AC2) ＝10.
∵点D是BC的中点，
∴CD＝ eq \f(1,2) BC＝5.
∵∠EDF＝90°，
第35题解图①
∴∠MDB＋∠1＝90°，
∵∠B＝∠MDB，
∴∠1＝∠C，
∴ND＝NC.
∵∠CGN＝90°.
∴CG＝ eq \f(1,2) CD＝ eq \f(5,2) .
∵∠C＝∠C，∠CGN＝∠CAB＝90°，
∴△CGN∽△CAB，
∴ eq \f(CG,CA) ＝ eq \f(CN,CB) ，即 eq \f(\f(5,2),8) ＝ eq \f(CN,10) ，∴CN＝ eq \f(25,8) ；
(3) eq \f(25,7) .
【解法提示】如解图②，延长ND到点H，使得DH＝DN，连接MN，BH，MH，∵D为BC的中点，∴DB＝DC，又∵∠BDH＝∠CDN，DH＝DN，∴△BDH≌△CDN，∴BH＝CN，∠BHD＝∠DNC，∴BH∥AC，∵∠BAC＝90°，∴∠ABH＝90°.设AM＝AN＝x，则MN＝ eq \r(2) x，BM＝6－x，CN＝BH＝8－x，∵MD⊥NH，DH＝DN，∴MN＝MH＝ eq \r(2) x.∵在Rt△MBH中，∠MBH＝90°，∴MH2＝BM2＋BH2，即( eq \r(2) x)2＝(6－x)2＋(8－x)2，解得x＝ eq \f(25,7) ，∴AN＝ eq \f(25,7) .
第35题解图②
36. D 【解析】∵四边形ABCD与四边形A′B′C′D′位似，∴四边形ABCD∽四边形A′B′C′D′，∴ eq \f(S四边形ABCD,S四边形A′B′C′D′) ＝( eq \f(OA,OA′) )2，∵S四边形ABCD＝2， eq \f(OA,OA′) ＝ eq \f(1,3) ，∴ eq \f(2,S四边形A′B′C′D′) ＝( eq \f(1,3) )2，解得S四边形A′B′C′D′＝18.
37. 2∶5
38. 解：(1)4；
【解法提示】点A、A′之间的距离为|2－(－2)|＝4.
(2)如解图，△A′B′C′即为所求作．
第38题解图
39. 解：(1)(1，1)，(0，4)，(2，2)；
(2)根据题意得∠BOB1＝90°，OB＝OB1＝4，
∴点B旋转到点B1的弧长为 eq \f(90π×4,180) ＝2π.
40. 解：(1)如解图所示，△A1B1C1即为所求；
(2)如解图所示，△A2B2C2即为所求．
点B2的坐标为(－4，－6).
第40题解图