2024中考数学全国真题分类卷 模型六 对角互补模型 强化训练(含答案)

这是一份2024中考数学全国真题分类卷 模型六 对角互补模型 强化训练(含答案)，共7页。试卷主要包含了∵BE＝4，∴CE＝9－4＝5等内容，欢迎下载使用。
1.如图，在菱形ABCD中，∠ABC是锐角，E是BC边上的动点，将射线AE绕点A按逆时针方向旋转，交直线CD于点F.当AE⊥BC，∠EAF＝∠ABC时．
(1)求证：AE＝AF；
(2)连接BD，EF，若 eq \f(EF,BD) ＝ eq \f(2,5) ，求 eq \f(S△AEF,S菱形ABCD) 的值．
第1题图
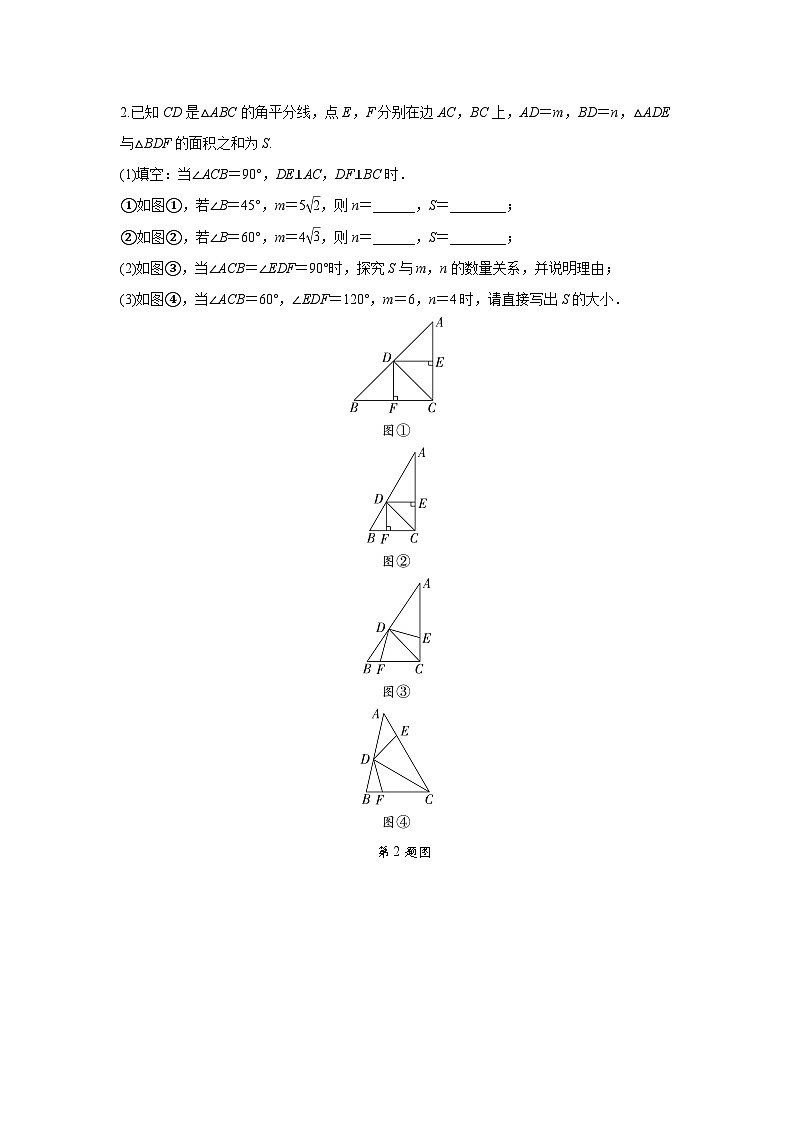
2.已知CD是△ABC的角平分线，点E，F分别在边AC，BC上，AD＝m，BD＝n，△ADE与△BDF的面积之和为S.
(1)填空：当∠ACB＝90°，DE⊥AC，DF⊥BC时．
①如图①，若∠B＝45°，m＝5 eq \r(2) ，则n＝______，S＝________；
②如图②，若∠B＝60°，m＝4 eq \r(3) ，则n＝______，S＝________；
(2)如图③，当∠ACB＝∠EDF＝90°时，探究S与m，n的数量关系，并说明理由；
(3)如图④，当∠ACB＝60°，∠EDF＝120°，m＝6，n＝4时，请直接写出S的大小．
第2题图
类型二 相似型
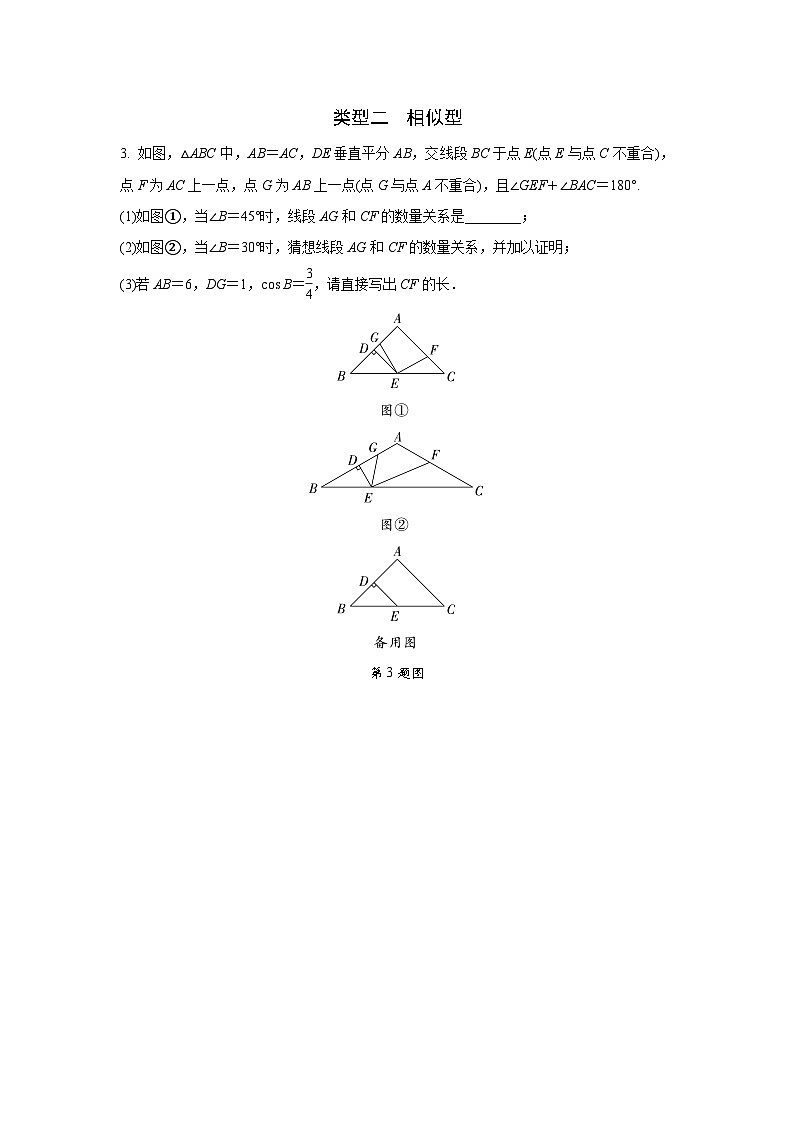
3. 如图，△ABC中，AB＝AC，DE垂直平分AB，交线段BC于点E(点E与点C不重合)，点F为AC上一点，点G为AB上一点(点G与点A不重合)，且∠GEF＋∠BAC＝180°.
(1)如图①，当∠B＝45°时，线段AG和CF的数量关系是________；
(2)如图②，当∠B＝30°时，猜想线段AG和CF的数量关系，并加以证明；
(3)若AB＝6，DG＝1，cs B＝ eq \f(3,4) ，请直接写出CF的长．
第3题图
参考答案与解析
1. (1)证明：在菱形ABCD中，AB＝AD，∠ABC＝∠ADC，AD∥BC，
∵AE⊥BC，∴AE⊥AD，
∴∠ABE＋∠BAE＝∠EAF＋∠DAF＝90°.
∵∠EAF＝∠ABC，
∴∠BAE＝∠DAF，
∴△ABE≌△ADF，
∴AE＝AF；
(2)解：如解图，连接AC.
第1题解图
由(1)知，△ABE≌△ADF，∴BE＝DF，∴CE＝CF，
∵AE＝AF，∴AC⊥EF.
在菱形ABCD中，AC⊥BD，∴EF∥BD，
∴△CEF∽△CBD，
∴ eq \f(EC,BC) ＝ eq \f(EF,BD) ＝ eq \f(2,5) ，
设EC＝2a，则AB＝BC＝5a，BE＝3a，∴AE＝4a.
∵AE＝AF，AB＝BC，
∴ eq \f(AE,AF) ＝ eq \f(BA,BC) ，
∵∠EAF＝∠ABC，
∴△AEF∽△BAC，
∴ eq \f(S△AEF,S△BAC) ＝( eq \f(AE,BA) )2＝( eq \f(4a,5a) )2＝ eq \f(16,25) ，
∴ eq \f(S△AEF,S菱形ABCD) ＝ eq \f(S△AEF,2S△BAC) ＝ eq \f(1,2) × eq \f(16,25) ＝ eq \f(8,25) .
2. 解：(1)①5 eq \r(2) ，25；
②4，8 eq \r(3) ；
(2)S＝ eq \f(1,2) mn.理由如下：
如解图①，过点D作DM⊥AC于点M，作DN⊥BC于点N，作DG⊥AB交BC的延长线于点G.
∵CD是△ABC的角平分线．
∴DM＝DN.
∵∠ACB＝∠EDF＝90°，
∴∠DFC＋∠DEC＝180°.
又∵∠DEM＋∠DEC＝180°，
∴∠DEM＝∠DFN，
∴△EDM≌△FDN(AAS).
∴DE＝DF，∠DEM＝∠DFN，
∵DG⊥AB，
∴∠ADG＝∠EDF＝90°.
即∠ADE＋∠EDG＝∠GDF＋∠EDG＝90°，
∴∠ADE＝∠GDF.
∴△ADE≌△GDF(ASA).
∴GD＝AD＝m，S△ADE＝S△GDF，
∴S＝S△ADE＋S△BDF＝S△DFG＋S△BDF＝S△BDG.
∵DG⊥BD，GD＝m，BD＝n，
∴S＝S△BDG＝ eq \f(1,2) mn；
第2题解图①
(3)S＝6 eq \r(3) .
【解法提示】如解图②，过点D作DM⊥AC于点M，DN⊥BC于点N.∵DM⊥AC，DN⊥BC，CD平分∠ACB，∴DM＝DN，∵∠DMC＝∠DNC＝90°，∴∠MDN＝180°－∠ACB＝120°，∴∠EDF＝∠MDN＝120°，∴∠EDM＝∠FDN，∵∠DME＝∠DNF＝90°，∴△DME≌△DNF，∴S＝S△ADE＋S△BDF＝S△ADM＋S△BDN，把△ADM绕点D顺时针旋转120°得到△TDN，则∠BDT＝60°，DT＝6，DB＝4，过点B作BH⊥DT于点H，∴BH＝BD·sin 60°＝4× eq \f(\r(3),2) ＝2 eq \r(3) ，∴S＝S△BDT＝ eq \f(1,2) ×6×2 eq \r(3) ＝6 eq \r(3) .
第2题解图②
3. 解：(1)AG＝CF；
【解法提示】如解图①，连接AE，∵DE垂直平分AB，∴AE＝BE，∴∠BAE＝∠B＝45°，∴AE⊥BC.∵AB＝AC，∴BE＝EC＝AE，∠BAE＝∠EAC＝∠C＝45°.∵∠GEF＋∠BAC＝180°，∴∠AGE＋∠AFE＝360°－180°＝180°.∵∠AFE＋∠CFE＝180°，∴∠AGE＝∠CFE.∵∠GAE＝∠C＝45°，∴△AEG≌△CEF(AAS)，∴AG＝CF.
第3题解图
(2)AG＝ eq \f(1,2) CF；
证明：如解图②，连接AE，
∵AB＝AC，
∴∠B＝∠C＝30°，
∴∠BAC＝120°.
∵DE垂直平分AB，
∴AE＝BE，
∴∠BAE＝∠B＝30°，
∴∠CAE＝90°，∠BAE＝∠C.
∵∠GEF＋∠BAC＝180°，
∴∠AGE＋∠AFE＝180°.
∵∠CFE＋∠AFE＝180°，
∴∠AGE＝∠CFE，
∴△AGE∽△CFE，
∴ eq \f(AG,CF) ＝ eq \f(AE,CE) ，
在Rt△ACE中，∵∠C＝30°，
∴ eq \f(AE,CE) ＝sin C＝ eq \f(1,2) ，∴ eq \f(AG,CF) ＝ eq \f(1,2) ，
∴AG＝ eq \f(1,2) CF；
(3)CF的长为 eq \f(5,2) 或5.
【解法提示】①当点G在线段DA上时，如解图③，连接AE，∵DE垂直平分AB，∴AD＝BD＝3，AE＝BE，∴∠BAE＝∠B.∵cs B＝ eq \f(BD,BE) ，∴BE＝ eq \f(BD,cs B) ＝ eq \f(3,\f(3,4)) ＝4，∴AE＝BE＝4，∵AB＝AC，∴∠B＝∠C，∴∠C＝∠BAE.∵∠GEF＋∠BAC＝180°，∴∠AGE＋∠AFE＝360°－180°＝180°.∵∠AFE＋∠CFE＝180°，∴∠CFE＝∠AGE，∴△CFE∽△AGE，∴ eq \f(CF,AG) ＝ eq \f(CE,AE) ，过点A作AH⊥BC于点H，∵cs B＝ eq \f(3,4) ，cs 45°＝ eq \f(\r(2),2) ，∵ eq \f(3,4) ＞ eq \f(\r(2),2) ，∴∠B＜45°，∴点E在点H的左侧．∵cs B＝ eq \f(BH,AB) ＝ eq \f(3,4) ，∴BH＝ eq \f(3,4) AB＝ eq \f(3,4) ×6＝ eq \f(9,2) .∵AB＝AC，∴BC＝2BH＝9.∵BE＝4，∴CE＝9－4＝5.∵AG＝AD－DG＝3－1＝2，∴ eq \f(CF,2) ＝ eq \f(5,4) ，∴CF＝ eq \f(5,2) ；②当点G在线段BD上时，如解图④，同①可得，△CFE∽△AGE，∴ eq \f(CF,AG) ＝ eq \f(CE,AE) .∵AG＝AD＋DG＝3＋1＝4，∴ eq \f(CF,4) ＝ eq \f(5,4) ，∴CF＝5.综上所述，CF的长为 eq \f(5,2) 或5.
第3题解图