
2024中考数学全国真题分类卷 模型四 手拉手模型 强化训练(含答案)
展开
这是一份2024中考数学全国真题分类卷 模型四 手拉手模型 强化训练(含答案),共8页。试卷主要包含了阅读材料等内容,欢迎下载使用。
1.阅读材料:小明喜欢探究数学问题,一天杨老师给他这样一个几何问题:
如图①,△ABC和△BDE都是等边三角形,点A在DE上.
求证:以AE、AD、AC为边的三角形是钝角三角形.
【探究发现】(1)小明通过探究发现:连接DC,根据已知条件,可以证明DC=AE,∠ADC=120°,从而得出△ADC为钝角三角形,故以AE、AD、AC为边的三角形是钝角三角形.
请你根据小明的思路,写出完整的证明过程;
【拓展迁移】(2)如图②,四边形ABCD和四边形BGFE都是正方形,点A在EG上.
①试猜想:以AE、AG、AC为边的三角形的形状,并说明理由;
②若AE2+AG2=10,试求出正方形ABCD的面积.
第1题图
类型二 相似型
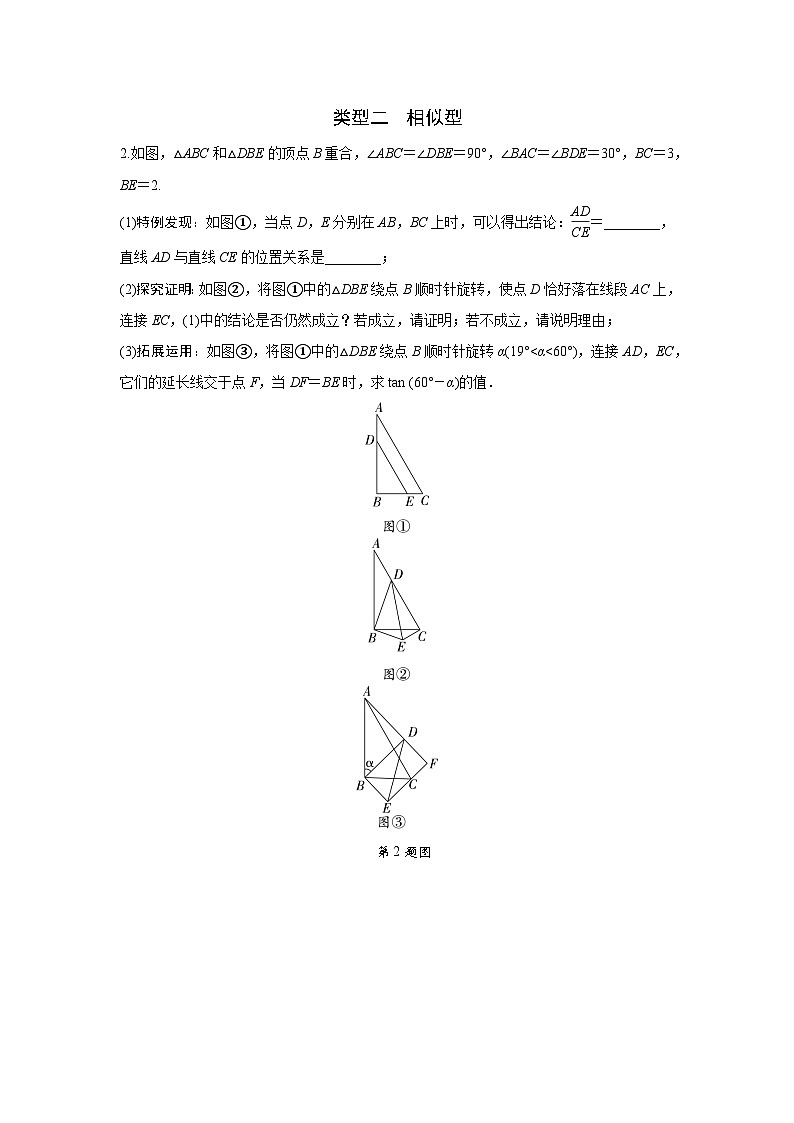
2.如图,△ABC和△DBE的顶点B重合,∠ABC=∠DBE=90°,∠BAC=∠BDE=30°,BC=3,BE=2.
(1)特例发现:如图①,当点D,E分别在AB,BC上时,可以得出结论: eq \f(AD,CE) =________,直线AD与直线CE的位置关系是________;
(2)探究证明:如图②,将图①中的△DBE绕点B顺时针旋转,使点D恰好落在线段AC上,连接EC,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;
(3)拓展运用:如图③,将图①中的△DBE绕点B顺时针旋转α(19°
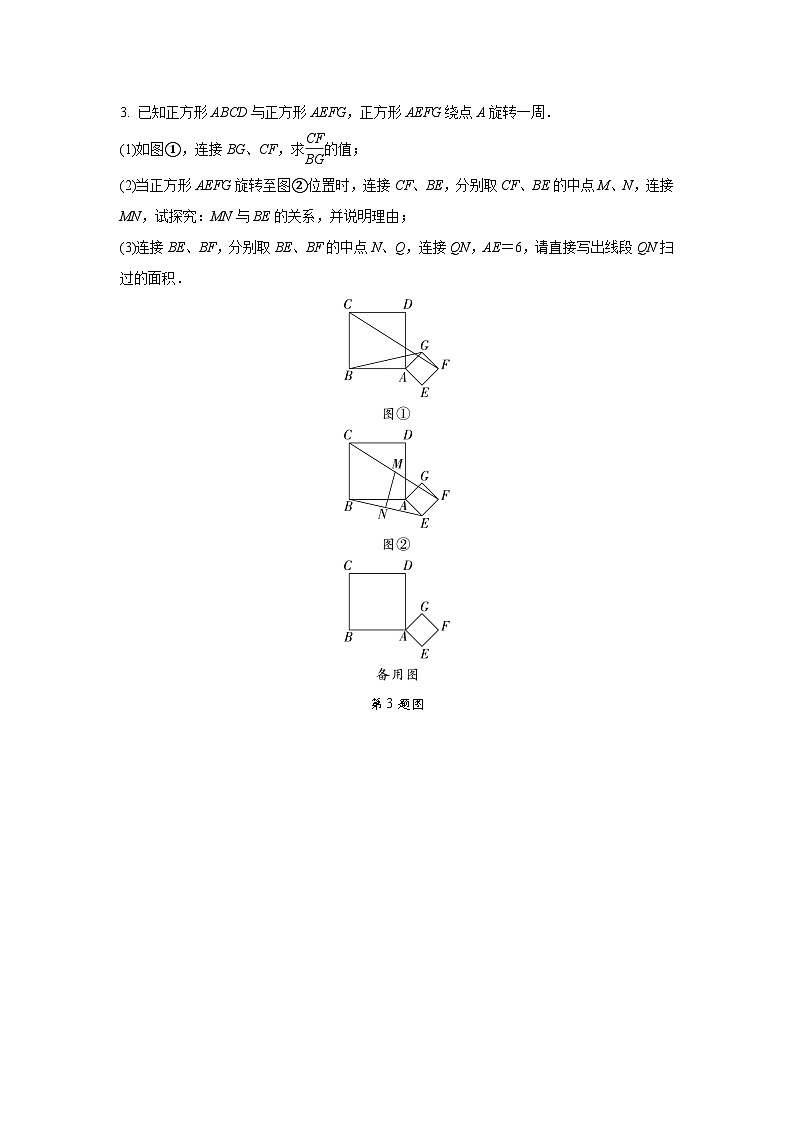
相关试卷
这是一份2024中考数学全国真题分类卷 模型二 截长补短模型 强化训练(含答案),共10页。
这是一份2024中考数学全国真题分类卷 模型八 利用两点之间线段最短求最值 强化训练(含答案),共10页。试卷主要包含了利用两点之间线段最短求最值等内容,欢迎下载使用。
这是一份15 全等与相似模型-手拉手模型-2024年中考数学几何模型归纳讲练(全国通用),文件包含15全等与相似模型-手拉手模型教师版docx、15全等与相似模型-手拉手模型学生版docx等2份试卷配套教学资源,其中试卷共80页, 欢迎下载使用。









