沪教版九年级上册数学专题训练九年级数学期中模拟卷(二)(原卷版+解析)

这是一份沪教版九年级上册数学专题训练九年级数学期中模拟卷(二)(原卷版+解析)，共27页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题(共18分)
1．已知线段 、 、 、 ，如果 ，那么下列式子中一定正确的是（ ）
A．B．C．D．
2．已知非零向量与，那么下列说法正确的是（ ）
A．如果，那么
B．如果，那么；
C．如果，那么；
D．如果，那么．
3．下列命题中，假命题的是（ ）
A．两个等边三角形一定相似；
B．两个全等三角形一定相似；
C．有一个锐角相等的两个直角三角形一定相似；
D．有一个锐角相等的两个等腰三角形一定相似．
4．如图，能推出 DE∥BC 的比例式是（ ）
A．B．
C．D．
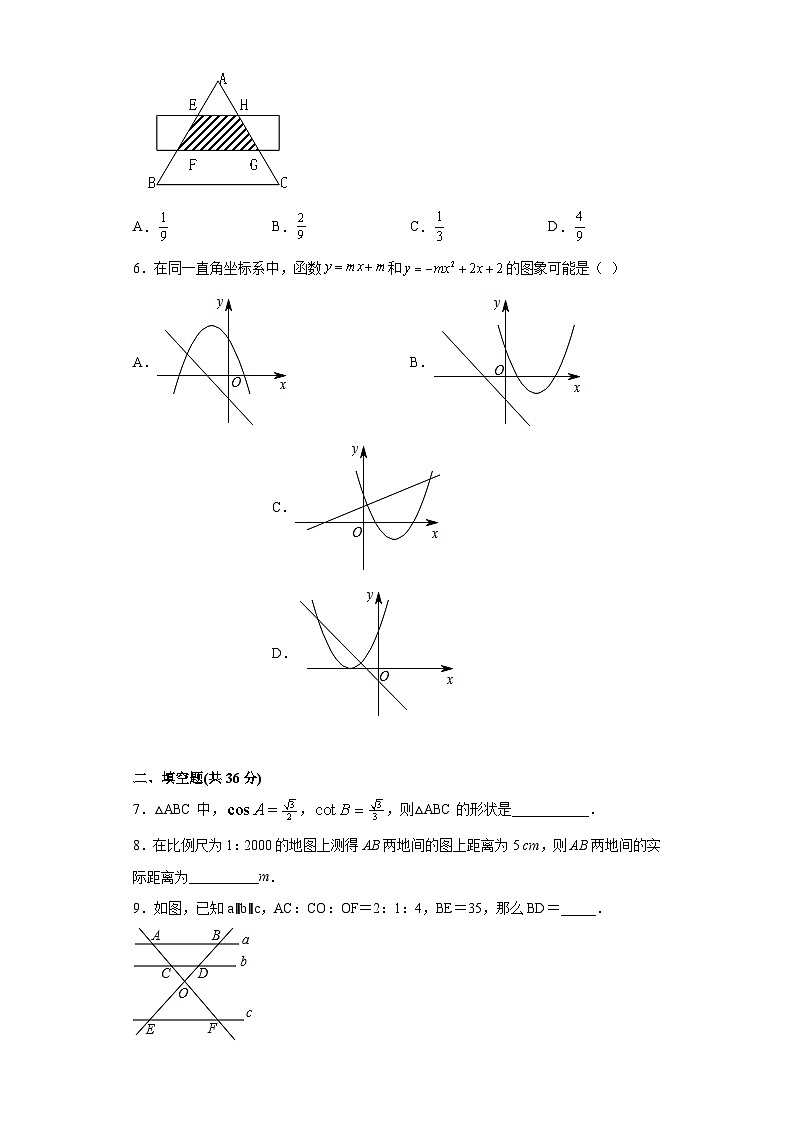
5．如图，是等边三角形，被一平行于的矩形所截(即：FG∥BC)，若AB被截成三等分，则图中阴影部分的面积是的面积的（ ）
A．B．C．D．
6．在同一直角坐标系中，函数和的图象可能是（ ）
A．B．C．D．
二、填空题(共36分)
7．△ABC中，，，则△ABC的形状是___________．
8．在比例尺为1：2000的地图上测得AB两地间的图上距离为5 cm，则AB两地间的实际距离为__________m．
9．如图，已知a∥b∥c，AC：CO：OF＝2：1：4，BE＝35，那么BD＝_____．
10．如图，△ABC中，DE∥FG∥BC，若AD＝DF＝FB，△ADE、梯形DEGF、梯形BCGF的面积分别为S1、S2、S3，则S1：S2：S3是_____．
11．计算： （_____________________）
12．将抛物线 y=x2﹣2 向上平移 3 个单位，所得抛物线的函数表达式为_________．
13．已知实数满足则__________．
14．已知，二次函数的部分对应值如下表，则________．
15．已知在Rt△ABC中，，tanA=，BC=6，则AB的长为__________．
16．在△ABC中，AB＝5，BC＝8，∠B＝60°，则S△ABC＝_____（结果保留根号）
17．如图，在△ABC 中，∠ABC＝90°，AB＝6，BC＝8．点 M、N分别在边 AB、 BC上，沿直线 MN将△ABC折叠，点 B落在点 P处，如果 AP∥BC且 AP=4，那么 BN=________．
18．如图D、E分别是AB、AC上的点，DE∥BC，△ABC的内角平分线AQ交DE于点P，过点P作直线交AB、AC于R、S，若，则DE=________．
三、解答题(共66分)
19．(本题6分)计算：cs245°＋ct230°.
20．(本题8分)如图，在平行四边形ABCD中，AC=AB．求证：∠ABD=∠DAC．
21．(本题10分)如图，在Rt△ABC中，∠ACB = 90°，BC = 6，AC = 8．点D是AB边上一点，过点D作DE // BC，交边AC于E．过点C作CF // AB，交DE的延长线于点F．
（1）如果，求线段EF的长；
（2）求∠CFE的正弦值．
22．(本题12分)如图，已知在△ABC中，AB=AC，BC比AB大3，，点G是△ABC的重心，AG的延长线交边BC于点D．过点G的直线分别交边AB于点P、交射线AC于点Q.
（1）求AG的长；
（2）当∠APQ=90º时，直线PG与边BC相交于点M.求的值；
（3）当点Q在边AC上时，设BP=x，AQ=y，求y关于x的函数解析式，并写出它的定义域.
23．(本题10分)如图，AD是△ABC中∠BAC的平分线，过A作AE⊥AD交BC的延长线于点E，M为DE的中点．
（1）求证：ME2＝MC•MB；
（2）如果BA2＝BD•BE，求证：
24．(本题10分)已知：如图，在□ABCD中，E、F分别是边 DC、BC上的点，且3BF 2BC ，DE 2CE ．
（1）求证：EF//BD；
（2）设 AB ， AD ，用向量 、 表示向量 ；
25．(本题10分)如图1是小明在健身器材上进行仰卧起坐锻炼时的情景，图2是小明锻炼时上半身由位置运动到与底面CD垂直的位置时的示意图，已知米，米，(参考数据：)
（1）求的长
（2）若米，求两点的距离（精确0.01)
2021-2022学年第一学期沪教版九年级期中模拟卷二
（解析版）
学校:___________姓名：___________班级：___________考号：___________
一、单选题(共18分)
1．已知线段 、 、 、 ，如果 ，那么下列式子中一定正确的是（ ）
A．B．C．D．
答案:C
【详解】
试题解析：∵ab=cd，
∴，．
故选C．
2．已知非零向量与，那么下列说法正确的是（ ）
A．如果，那么
B．如果，那么；
C．如果，那么；
D．如果，那么．
答案:D
分析：
根据向量的定义可直接进行排除选项．
【详解】
A、如果，与的大小相等，但方向不一定相同，故错误；
B、如果，与的大小相等，但不一定平行，故错误；
C、如果，与的大小不一定相等，故错误；
D、如果，那么，故正确；
故选D．
【点睛】
本题主要考查向量，正确理解向量的定义是解题的关键．
3．下列命题中，假命题的是（ ）
A．两个等边三角形一定相似；
B．两个全等三角形一定相似；
C．有一个锐角相等的两个直角三角形一定相似；
D．有一个锐角相等的两个等腰三角形一定相似．
答案:D
分析：
根据真命题和假命题的定义判断出各题的真假即可．
【详解】
解：两个等边三角形，三角相等，一定相似，A是真命题；
有一个锐角相等的两个直角三角形，三角相等，一定相似，B是真命题；
全等三角形是特殊的相似三角形，C是真命题；
有一个锐角相等的两个等腰三角形，其它两角不一定相等，不能判定这两个三角形相似．
故选：D．
【点睛】
本题主要考查了命题与定理，正确的命题叫真命题，错误的命题叫做假命题．熟练掌握各定理是解题的关键.．
4．如图，能推出 DE∥BC 的比例式是（ ）
A．B．
C．D．
答案:C
分析：
由DE∥BC，根据平行线分线段成比例定理，可得，继而可求得答案，注意排除法在解选择题中的应用．
【详解】
解： A.由，不能推出DE∥BC，故A错误；
B.由，不能推出DE∥BC，故B错误；
C.因为，∠BAC=∠DAE，所以△ABC∽△ADE.所以∠B=∠D，所以DE∥BC，故C正确；
D.由不能推出DE∥BC，故D错误.
故选：C．
【点睛】
本题考查了平行线分线段成比例定理．注意掌握数形结合思想的应用，注意掌握线段的对应关系．
5．如图，是等边三角形，被一平行于的矩形所截(即：FG∥BC)，若AB被截成三等分，则图中阴影部分的面积是的面积的（ ）
A．B．C．D．
答案:C
分析：
AB被截成三等分，可得AB=3AE，AF=2AE，由EH∥FG∥BC，可得△AEH∽△AFG∽△ABC，则S△AEH：S△AFG：S△ABC=AE2：AF2：AB2，S阴影= S△AFG- S△AEH =S△ABC．
【详解】
∵AB被截成三等分，
∴AB=3AE，AF=2AE，
∵EH∥FG∥BC，
∴△AEH∽△AFG∽△ABC，
∴S△AEH：S△AFG：S△ABC=AE2：AF2：AB2=AE2：（2AE）2：（3AE）2=1:4:9，
∴S△AEH= S△ABC, S△AFG=4 S△AEH，
S阴影= S△AFG- S△AEH=3 S△AEH=3× S△ABC=S△ABC．
故选择：C．
【点睛】
本题考查阴影部分面积问题，关键是利用相似三角形的面积比等于相似比的平方，找到阴影面积与△AEH的关系，由△AEH与△ABC的关系来转化解决问题．
6．在同一直角坐标系中，函数和的图象可能是（ ）
A．B．C．D．
答案:D
分析：
根据的符号，针对二次函数、一次函数的图象位置，开口方向，分类讨论，逐一判断即可．
【详解】
A：由函数的图像可知，即函数开口应向上，与图像不符，故A错误；
B、由函数的图像可知，函数的对称轴，则对称轴应在轴的左侧与图像不符，故B错误；
C：由函数的图像可知，即函数开口应向下，与图像不符，故C错误；
D：由函数的图像可知，即函数开口向上，函数的对称轴，则对称轴应在轴的左侧与图像相符，故D正确；
故选：D．
【点睛】
本题主要考查了一次函数与二次函数图象，关键是熟练掌握一次函数y=kx+b在不同情况下所在的象限，以及熟练掌握二次函数的有关性质：开口方向、对称轴、顶点坐标等．
二、填空题(共36分)
7．△ABC中，，，则△ABC的形状是___________．
答案:直角三角形
分析：
根据特殊的三角函数值，求得∠A，∠B的度数，再进行判断．
【详解】
∵，，
∴ ∠A＝30°，∠B＝60°，
∴∠C＝180°－∠A－∠B＝90°，
故△ABC是直角三角形，
故填：直角三角形．
【点睛】
本题考查特殊的三角函数值，熟练记忆是关键．
8．在比例尺为1：2000的地图上测得AB两地间的图上距离为5 cm，则AB两地间的实际距离为__________m．
答案:100
解析：
试题分析：设AB两地间的实际距离为x，
，
解得x=10000cm=100m．
故答案为100m．
考点：比例线段．
9．如图，已知a∥b∥c，AC：CO：OF＝2：1：4，BE＝35，那么BD＝_____．
答案:10
分析：
根据平行线分线段成比例定理即可得出结论．
【详解】
解：∵a∥b∥c，
∴BD：BE＝AC：AF，
∵AC：CO：OF＝2：1：4，
∴AC：AF＝2：7，
∴BD：BE＝2：7，
∴BD＝BE＝×35＝10，
故答案为10．
【点睛】
此题考查的是平行线分线段成比例定理,根据平行线分线段成比例定理列比例式是解决此题的关键.
10．如图，△ABC中，DE∥FG∥BC，若AD＝DF＝FB，△ADE、梯形DEGF、梯形BCGF的面积分别为S1、S2、S3，则S1：S2：S3是_____．
答案:1：3：5
分析：
根据△ADE∽△AFG，得到＝（）2＝，再根据△ADE∽△ABC，得到＝（）2＝，计算得到答案．
【详解】
解：∵DE∥FG，
∴△ADE∽△AFG，
∴＝（）2＝，
∴S1：S2＝1：3，
∵DE∥BC，
∴△ADE∽△ABC，
∴＝（）2＝，
∴S1：S四边形DBCE＝1：8，
∴S1：S2：S3＝1：3：5，
故答案为：1：3：5．
【点睛】
此题考查的是相似三角形的性质, 掌握相似三角形的面积比等于相似比的平方是解决此题的关键.
11．计算： （_____________________）
答案:
分析：
实数的运算法则同样适用于平面向量的计算，由有理数混合运算法则解答即可．
【详解】
=
故答案为：
【点睛】
考查了平面向量，属于基础计算题．乘法分配律也同样适用于平面向量的计算．
12．将抛物线 y=x2﹣2 向上平移 3 个单位，所得抛物线的函数表达式为_________．
答案:
分析：
根据函数的平移规律“上加下减”的原则进行解答即可．
【详解】
解：根据函数的平移规律“上加下减”的原则可知，
将抛物线y=x2-2向上平移3个单位，所得抛物线的函数表达式为y=x2-2+3，即y=x2+1，
故答案为：y=x2+1．
【点睛】
本题考查的是二次函数的图象与几何变换，熟练掌握函数的平移规律“上加下减，左加右减”的原则是解答此题的关键．
13．已知实数满足则__________．
答案:2
分析：
由于给了，设x=3m，则y=2m，将x，y代入计算即可．
【详解】
∵，
设x=3m，则y=2m，
=2．
故答案为：2．
【点睛】
本题考查比值问题，关键是把x，y转化为统一字母来表示．
14．已知，二次函数的部分对应值如下表，则________．
答案:12
分析：
根据二次函数的对称性结合图表数据可知，x＝−3时的函数值与x＝5时的函数值相同．
【详解】
由图表数据可知，抛物线的对称轴为：x=1
且f（−3）＝f（5）＝12．
故答案为12．
【点睛】
本题考查了二次函数的性质，主要利用了二次函数的对称性，理解图表并准确获取信息是解题的关键．
15．已知在Rt△ABC中，，tanA=，BC=6，则AB的长为__________．
答案:
分析：
先根据tanA的定义和它的值求出AC，然后根据勾股定理即可求出答案．
【详解】
解：∵，tanA==，BC=6，
∴AC=8，
根据勾股定理得AB===10，
故答案为：10．
【点睛】
本题考查了锐角三角函数，勾股定理，求出AC的值是解题关键．
16．在△ABC中，AB＝5，BC＝8，∠B＝60°，则S△ABC＝_____（结果保留根号）
答案:
分析：
先根据AB＝5，∠B＝60°，求出△ABC中BC边上的高，再根据三角形的面积公式代入计算即可．
【详解】
解：∵AB＝5，∠B＝60°，
∴△ABC中，BC边上的高＝sin60°×AB＝×5＝，
∵BC＝8，
∴S△ABC＝×8×＝10；
故答案为：10．
【点睛】
此题考查了解直角三角形，关键是利用解直角三角形求出BC边上的高，用到的知识点是解直角三角形、三角形的面积公式，难度不大．
17．如图，在△ABC 中，∠ABC＝90°，AB＝6，BC＝8．点 M、N分别在边 AB、 BC上，沿直线 MN将△ABC折叠，点 B落在点 P处，如果 AP∥BC且 AP=4，那么 BN=________．
答案:
分析：
证明∠MBO=∠BNO；求出BP、BO的长度；证明△ABP∽△OBN，列出比例式即可解决问题．
【详解】
解：如图，连接BP，交MN于点O；
则BO=PO，BO⊥MN；
∵∠ABC=90°，
∴∠MBO+∠NBO=∠NBO+∠BNO，
∴∠MBO=∠BNO；
∵AP∥BC，且∠ABC=90°，
∴∠BAP=90°；
由勾股定理得：BP2=AB2+AP2，
∵AB=6，AP=4，
∴BP==2 ，BO=，
∵∠ABP=∠BNO，
∴△ABP∽△OBN，
∴ ，即，
解得：BN=．
故答案为：．
【点睛】
该题主要考查了翻折变换的性质、勾股定理、相似三角形的判定与性质等知识,掌握灵活运用勾股定理、相似三角形的判定及其性质等知识进行解答是解题的关键．
18．如图D、E分别是AB、AC上的点，DE∥BC，△ABC的内角平分线AQ交DE于点P，过点P作直线交AB、AC于R、S，若，则DE=________．
答案:6
分析：
由 ，且∠RAS=∠CAB，可证得△ARS∽△ACB，所以∠ARS=∠ACB，再由∠BAP=CAQ可证得△ARP∽△ACQ，，再由DE∥BC，可知，把BC的值代入可求得DE．
【详解】
解：∵，且∠RAS=∠CAB，
∴△ARS∽△ACB，
∴∠ARS=∠ACB，
又∵AQ为角平分线，
∴∠BAP=CAQ，
∴△ARP∽△ACQ，
∴，
∵DE∥BC，
∴，
∵BC=9，
∴，
∴DE=6．
【点睛】
本题主要考查三角形相似的判定和性质，解题的关键是能利用条件两次证得三角形相似，从而得到DE和BC的比值．
三、解答题(共66分)
19．(本题6分)计算：cs245°＋ct230°.
答案:.
分析：
把各特殊角度的三角函数值代入进行计算即可．
【详解】
原式＝2＋()2
＝＋3
＝.
【点睛】
本题考查特殊角的三角函数值，解题关键是熟记各特殊角度的三角函数值．
20．(本题8分)如图，在平行四边形ABCD中，AC=AB．求证：∠ABD=∠DAC．
答案:见解析．
分析：
根据AC＝AB证明，从而可证得△AOB∽△ABC，得对应角相等，同时再利用平行线所截的内错角相等得出结论．
【详解】
证明：∵四边形ABCD是平行四边形，
∴AC＝2AO，AD∥BC，
∵AC＝AB，
∴AO＝AB，
∴，
∵，
∴，
∵∠CAB＝∠CAB，
∴△AOB∽△ABC，
∴∠ABD＝∠ACB，
∵AD∥BC，
∴∠ACB＝∠DAC，
∴∠ABD＝∠DAC．
【点睛】
本题考查了平行四边形的性质，熟练掌握平行四边形边、角、对角线的关系；在证明两角相等时，除了运用平行线、全等三角形外，还可以证明两三角形相似，得对应角相等．
21．(本题10分)如图，在Rt△ABC中，∠ACB = 90°，BC = 6，AC = 8．点D是AB边上一点，过点D作DE // BC，交边AC于E．过点C作CF // AB，交DE的延长线于点F．
（1）如果，求线段EF的长；
（2）求∠CFE的正弦值．
答案:（1）4；（2）.
分析：
（1）根据相似三角形的性质得到 ，求得DE=2，推出四边形BCFD是平行四边形，根据平行四边形的性质得到DF=BC=6，于是得到结论；
（2）根据平行四边形的性质得到∠B=∠F，根据勾股定理得，根据三角函数的定义即可得到结论．
【详解】
解：（1）∵ DE // BC，∴ ．
又∵ BC = 6，∴ DE = 2．
∵ DF // BC，CF // AB，∴ 四边形BCFD是平行四边形．
∴ DF = BC = 6．∴ EF = DF – DE = 4．
（2）∵ 四边形BCFD是平行四边形， ∴ ∠B =∠F．
在Rt△ABC中，∠ACB = 90°，BC = 6，AC = 8，
利用勾股定理，得．
∴ ．∴ ．
【点睛】
本题考查了相似三角形的判定和性质，平行四边形的性质，勾股定理，熟练掌握相似三角形的判定和性质是解题的关键．
22．(本题12分)如图，已知在△ABC中，AB=AC，BC比AB大3，，点G是△ABC的重心，AG的延长线交边BC于点D．过点G的直线分别交边AB于点P、交射线AC于点Q.
（1）求AG的长；
（2）当∠APQ=90º时，直线PG与边BC相交于点M.求的值；
（3）当点Q在边AC上时，设BP=x，AQ=y，求y关于x的函数解析式，并写出它的定义域.
答案:(1)AG=8；（2）；(3).
分析：
（1）根据已知条件和重心的性质得出BD=DC=BC，AD⊥BC，再根据sinB=，求出AB、BC、AD的值，从而求出AG的长；
（2）根据∠GMD+∠MGD=90°和∠GMD+∠B=90°，得出∠MGD=∠B，再根据特殊角的三角函数值求出DM、CM=CD-DM的值，在△ABC中，根据AA求出△QCM∽△QGA，即可求出的值；
（3）过点B作BE∥AD，过点C作CF∥AD，分别交直线PQ于点E、F，则BE∥AD∥CF，得出，求出BE的值，同理可得出CF的值，最后根据BD=CD，求出EG=FG，即可得出CE+BE=2GD，从而得出求y关于x的函数解析式并得出它的定义域．
【详解】
（1）在△ABC中，∵AB=AC，点G是△ABC的重心,
∴，AD⊥BC.
在Rt△ADB中，∵,∴.
∵, ∴AB=15，BC=18.
∴AD="12."
∵G是△ABC的重心，∴.
（2）在Rt△MDG,∵∠GMD+∠MGD=90°，
同理:在Rt△MPB中,∠GMD+∠B=90°,
∴∠MGD=∠B.
∴,
在Rt△MDG中,∵，
∴，∴
在△ABC中，∵AB=AC，AD⊥BC,∴.
∵,
又∵,
∴,
又∵,
∴△QCM∽△QGA.
∴.
（3）过点作,过点作,分别交直线于点E、F，则.
∵,∴,即,
∴
同理可得:,即,
∴.
∵,,∴.
∴,即.
∴,.
23．(本题10分)如图，AD是△ABC中∠BAC的平分线，过A作AE⊥AD交BC的延长线于点E，M为DE的中点．
（1）求证：ME2＝MC•MB；
（2）如果BA2＝BD•BE，求证：
答案:（1）见解析；（2）见解析.
分析：
（1）证明△AMC∽△BMA即可解决问题．
（2）由△AMC∽△BMA，推出＝，推出＝，推出＝，再证明△BAC∽△BMA，推出＝，推出AB2＝BC•BM，即可解决问题．
【详解】
（1）证明：∵AE⊥AD，
∴∠DAE＝90°，
∵DM＝ME，
∴AM＝MD＝ME，
∴∠MAD＝∠MDA，
∴∠MAC+∠DAC＝∠B+∠BAD，
∵∠BAD＝∠CAD，
∴∠MAC＝∠B，
∵∠AMC＝∠AMB，
∴△AMC∽△BMA，
∴＝，
∴AM2＝MC•MB，
∵ME＝MA，
∴ME2＝MC•MB．
（2）证明：∵△MAC∽△BMA，
∴＝，
∴＝，
∴＝，
∵AB2＝BD•BE，
∴＝，
∵∠B＝∠B，
∴△BAD∽△BEA，
∴∠BAD＝∠E，
∵∠AMB＝∠E+∠MAE＝2∠E，∠BAC＝2∠BAD，
∴∠BAC＝∠AMB，∵∠B＝∠B，
∴△BAC∽△BMA，
∴＝，
∴AB2＝BC•BM，
∴＝＝．
【点睛】
此题考查的是相似三角形的判定及性质，根据相似三角形的列比例式并改写比例式是解决此题的关键.
24．(本题10分)已知：如图，在□ABCD中，E、F分别是边 DC、BC上的点，且3BF 2BC ，DE 2CE ．
（1）求证：EF//BD；
（2）设 AB ， AD ，用向量 、 表示向量 ；
答案:(1)见解析；(2)
分析：
（1）根据平行线截线段成比例进行求证；
（2）利用三角形法则首先求得向量 ，然后用向量,表示向量．
【详解】
（1）∵
∴
∵
∴
∴
∴
∴
（2）解：由（1）知，EF∥BD，=，易得FE=DB．
∵AB= ，AD=，
∴=-+
∴
【点睛】
考查了平面向量和平行四边形的性质，解答（2）题时，利用平行线截线段成比例求得线段EF的长度是解题的关键．
25．(本题10分)如图1是小明在健身器材上进行仰卧起坐锻炼时的情景，图2是小明锻炼时上半身由位置运动到与底面CD垂直的位置时的示意图，已知米，米，(参考数据：)
（1）求的长
（2）若米，求两点的距离（精确0.01)
答案:（1）0.8；（2）1.04 m
分析：
（1）已知AC与BD，求AB，为此过D作BE⊥AC于E，可求AE，由∠ABE已知，利用30角所对直角．边等于斜边的一半，可求AB即可，
（2）过N作NF⊥MO交射线MO于F点，则FN∥EB，∠ONF=α=30°，利用外角有∠M=∠MNO=∠FON=30º，在30 º Rt△OFN 中，OF=ON，易求MF，利用Rt△MFN中MN=即可．
【详解】
（1）过B作BE⊥AC于E，则四边形CDBE为矩形，CE=BD=0.26米，AC=0.66米，
∴AE=AC-EC=0.66-0.26=0.40米，
在Rt△AEB中，α=30°，AB=2AE=2×0.40=0.80米，
（2）过N作NF⊥MO交射线MO于F点，则FN∥EB，
∴∠ONF=α=30°，
∵ON=0,6米，
∴OF=ON=0,3米，
∵OM=ON=0.6米，
∴MF=0.9米，
∴∠FON=90º-30º=60º，
∴∠M=∠MNO=∠FON=30º，
在Rt△MFN中，
MN=．
【点睛】
本题考查求斜面长，MN长，关键是掌握把要求的线段置于Rt △中,用三角函数来解决问题．