福建省南平市2023-2024学年高一下学期期末质量检测数学试题

这是一份福建省南平市2023-2024学年高一下学期期末质量检测数学试题，共9页。试卷主要包含了已知向量，，若，则等内容，欢迎下载使用。

（考试时间：120分钟 满分：150分）
注意事项：
1．答卷前，考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名、班级和座号。考生要认真核对答题卡上粘贴条形码的“准考证号、姓名”。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。
第Ⅰ卷（选择题部分）
一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．已知复数，则z在复平面内对应的点位于
A．第一象限 B．第二象限 C．第三象限 D．第四象限
2．如图，水平放置的△ABC用斜二测画法画出的直观图为△A'B'C'，其中，，，则△ABC中，AC＝
A．2 B． C． D．4
3．抛掷两枚质地均匀的硬币，设事件A＝“至多有一枚硬币正面朝上”，事件B＝“两枚硬币正面均朝上”，事件C＝“两枚硬币正面均朝下”，则
A．A与C对立 B．B与C不互斥 C．A与B互斥 D．B与C对立
4．已知向量，，若，则
A． B．1 C． D．2
5．已知α，β为两个不重合的平面，l，m为两条不同的直线，
A．若，，则 B．若，，则
C．若，，则 D．若，，则
6．在△ABC中，，点E是线段AD的中点，则
A． B．
C． D．
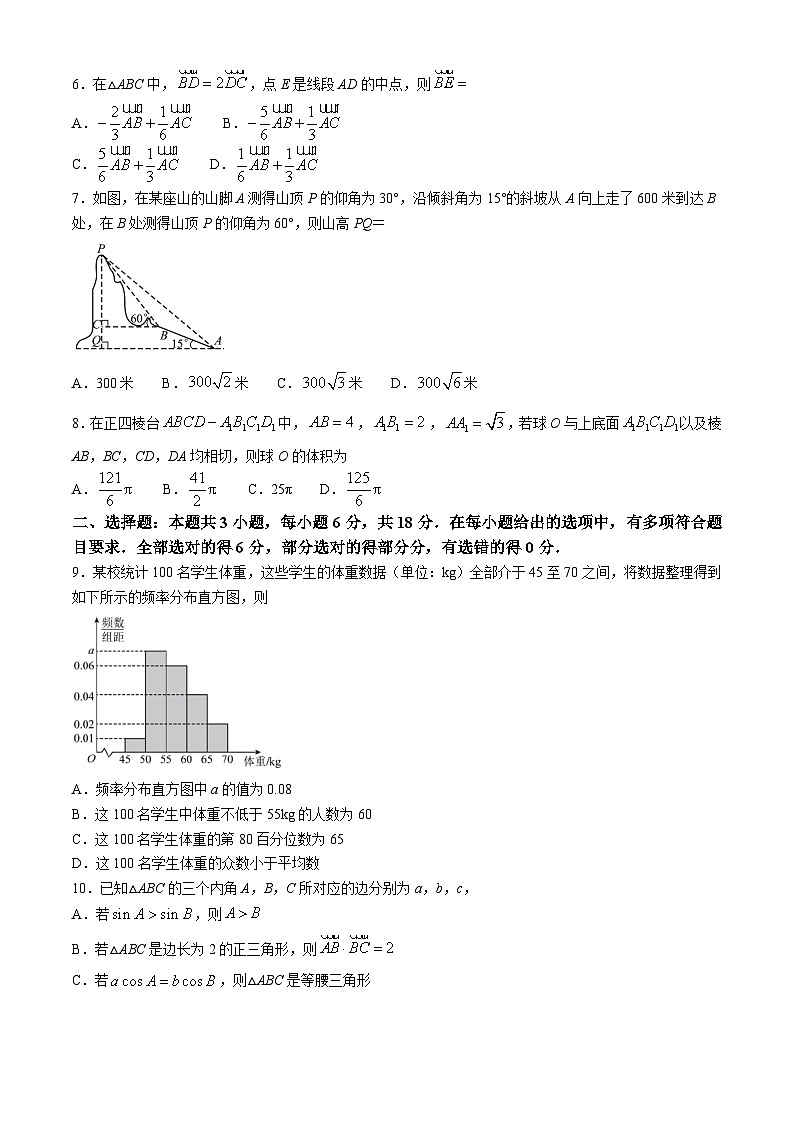
7．如图，在某座山的山脚A测得山顶P的仰角为30°，沿倾斜角为15°的斜坡从A向上走了600米到达B处，在B处测得山顶P的仰角为60°，则山高PQ＝
A．300米 B．米 C．米 D．米
8．在正四棱台中，，，，若球O与上底面以及棱AB，BC，CD，DA均相切，则球O的体积为
A． B． C．25π D．
二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．
9．某校统计100名学生体重，这些学生的体重数据（单位：kg）全部介于45至70之间，将数据整理得到如下所示的频率分布直方图，则
A．频率分布直方图中a的值为0.08
B．这100名学生中体重不低于55kg的人数为60
C．这100名学生体重的第80百分位数为65
D．这100名学生体重的众数小于平均数
10．已知△ABC的三个内角A，B，C所对应的边分别为a，b，c，
A．若，则
B．若△ABC是边长为2的正三角形，则
C．若，则△ABC是等腰三角形
D．若，BC的中线AD长为1，则bc的最大值为
11．如图，圆锥的顶点为S，底面圆心为O，AB为底面直径，，，N是底面圆周上一点，，M是线段SA上的动点，则
A．圆锥SO的体积为
B．当M是SA的中点时，线段MN在圆锥底面上的射影长为
C．存在点M，使得
D．直线MN与平面SAB所成角的正切值的最大值为
第Ⅱ卷（非选择题部分）
三、填空题：本题共3小题，每小题5分，共15分．
12．已知向量，，则在上的投影向量的坐标是________．
13．从长度为1，3，5，7，9的5条线段中任取3条，则这三条线段能构成一个三角形的概率是________．
14．如图，在棱长为6的正方体中，M，N分别为棱，的中点，则过M，N，B三点的平面截此正方体所得截面的周长是________．
四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．
15．（13分）
已知复数（，），为纯虚数，且．
（1）求复数z；
（2）若复数z是关于x的方程的一个根，求实数m，n的值．
16．（15分）
现有3个北方城市，，和3个南方城市，，，旅游爱好者甲计划从中任选2个城市旅游．
（1）求甲选择的2个城市均是北方城市的概率；
（2）若旅游爱好者乙也计划从这6个城市中选2个旅游，由于个人爱好，乙选择的2个城市均是北方城市的概率为，且甲、乙两人的选择互不影响，求甲、乙两人中至少有一人的选择为2个北方城市的概率．
17．（15分）
已知△ABC的三个内角A，B，C所对应的边分别为a，b，c，且．
（1）求A；
（2）若，且△ABC的面积为，求△ABC的周长．
18．（17分）
如图，在正方形ABCD中，点E，F分别是AB，CD的中点．现将△ADE沿DE折起，得到四棱锥A-BCDE．
（1）证明：；
（2）当△ACD为等边三角形时，证明：；
（3）在（2）的条件下，求二面角A-DE-C的余弦值．
19．（17分）
某校高一年级有男生200人，女生100人．为了解该校全体高一学生的身高信息，按性别比例进行分层随机抽样，抽取总样本量为30的样本，并观测样本的指标值（单位：cm），计算得男生样本的身高平均数为169，方差为39．下表是抽取的女生样本的数据：
记抽取的第i个女生的身高为（），样本平均数，方差．
参考数据：，，．
（1）若用女生样本的身高频率分布情况代替该校高一女生总体的身高频率分布情况，试估计该校高一女生身高在[160，165]范围内的人数；
（2）如果女生样本数据在之外的数据称为离群值，试剔除离群值后，计算剩余女生样本身高的平均数与方差；
（3）用总样本的平均数和标准差分别估计该校高一学生总体身高的平均数和标准差，求，的值．
南平市2023—2024学年第二学期高一年级期末质量检测
数学参考答案及评分标准
说明：
1、本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则．
2、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分．
3、只给整数分数．选择题和填空题不给中间分
一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．A 2．A 3．C 4．B 5．D 6．B 7．B 8．D
二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．
9．BD 10．AD 11．BCD
三、填空题：本题共3小题，每小题5分，共15分．
12． 13． 14．
四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．
15．（本题满分13分）
解：（1）因为（且），
且为纯虚数，
于是，且，即，且．
又，故，
因为，所以，于是，
因此复数．
（2）方法1：由（1）知，代入方程，得，化简得，
因为，所以，解得，因此实数，．
方法2：由（1）知，故是关于x的方程的另一个根，
所以由韦达定理得，，，
即，，因此实数，．
16．（本题满分15分）
解：（1）由题意知，从6个城市中任选2个，得到的样本空间为，
则．
设事件A＝“甲选择的2个城市均是北方城市”，
则，所以．
因此，．
（2）设事件C＝“甲、乙两人中至少有一人的选择为2个北方城市”，事件A＝“甲选择的2个城市均是北方城市”，事件B＝“乙选择的2个城市均是北方城市”．
则“甲选择的2个城市不都是北方城市”，“乙选择的2个城市不都是北方城市”，由于甲、乙的选择互不影响，所以A与B，A与，与B，与
都相互独立．
由已知条件及（1）可得，，，，．
方法1：因为，且AB，，两两互斥，
所以
．
．
方法2：由对立事件的性质可知，因为，所以
．
17．（本题满分15分）
解：（1）由正弦定理，得
，
所以，
即，
因为，所以，
从而，化简得，即，
又由，可得，
故，所以．
（2）由已知可得，，
可得，化简得，，即．
又由余弦定理知，，化简得，．
联立解得，，
所以△ABC的周长为．
18．（本题满分17分）
解：（1）证明：在正方形ABCD中，点E，F分别是AB，CD的中点，
所以，且，
故四边形BEDF为平行四边形，于是．
在四棱锥A-BCDE中，，，
所以．
（2）当△ACD为正三角形时，因为点F分别是CD的中点，所以．
在正方形ABCD中，点E，F分别是AB，CD的中点，故．
又，，，故．
因为，所以．
（3）在四棱锥A-BCDE中，过点A作于点O，过点O作于点G，连接AG．
在正方形ABCD中，令，则，．因为△ACD为等边三角形，点F为CD的中点，所以，从而，即．
由（2）知，，，
，故，从而．
又，，，，
故，而，故，
所以为二面角A-DE-C的平面角．
在Rt△EAF中，，．
在Rt△DEF中，，．
因为，所以，于是，
从而在Rt△AOG中，，
故，
因此，二面角A-DE-C的余弦值为．
19．（本题满分17分）
解：（1）抽取的女生身高的在[160，165]之内的频率为，
估计该校女生身高的在[160，165]之内的人数为．
（2）因为，，所以，
故，则169为离群值．
剔除离群值剩下数据的平均数为：，故剩余女生样本身高的平均数为159，
又，剔除169，剩余女生样本身高的方差为：，所以剩余女生样本身高的方差为．
（3）采用分层抽样的方法抽取一个容量为30的样本，则男生20个，女生10个，男生身高样本记为，，…，，均值，方差，女生身高样本为，，…，，均值，方差．
则总样本均值，
又因为，所以，同理可得，
故总样本方差
，
所以，估计学生总体身高的平均数，标准差．抽取次序
1
2
3
4
5
6
7
8
9
10
身高
155
158
156
157
160
161
159
162
169
163