人教版八年级上册12.3 角的平分线的性质精品教学作业课件ppt

这是一份人教版八年级上册12.3 角的平分线的性质精品教学作业课件ppt，文件包含人教版数学八年级上册1231角的平分线的性质教学课件含动画演示pptx、人教版八年级数学上册1231角的平分线的性质教学设计docx、人教版八年级数学上册1231角的平分线的性质分层作业原卷版docx、人教版八年级数学上册1231角的平分线的性质分层作业解析版docx、人教版八年级数学上册1231角的平分线的性质导学案docx等5份课件配套教学资源，其中PPT共25页， 欢迎下载使用。

情境导入Cntext intrductin
知识精讲Knwledge-based lecture
针对训练Fr training
典例解析Analysis f examples
达标测试Test t meet standards
小结梳理Summary and cmbing
1.通过操作、验证等方式，探究并掌握角平分线的性质定理.（难点）2.能运用角的平分线性质解决简单的几何问题. （重点）
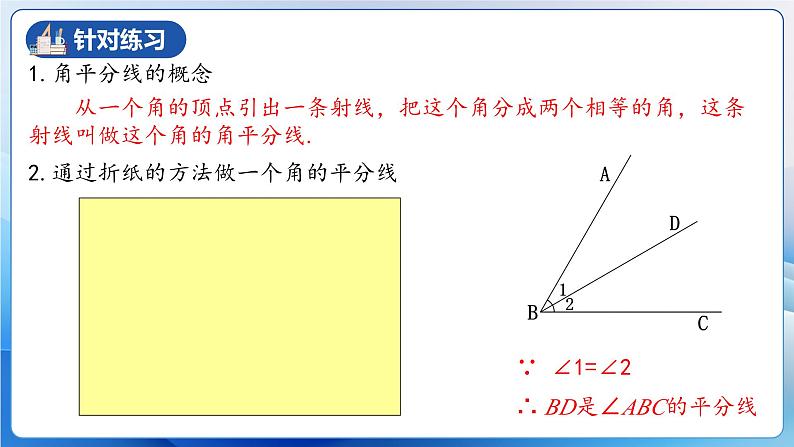
从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的角平分线.
∵ ∠1=∠2 ∴ BD是∠ABC的平分线
2.通过折纸的方法做一个角的平分线
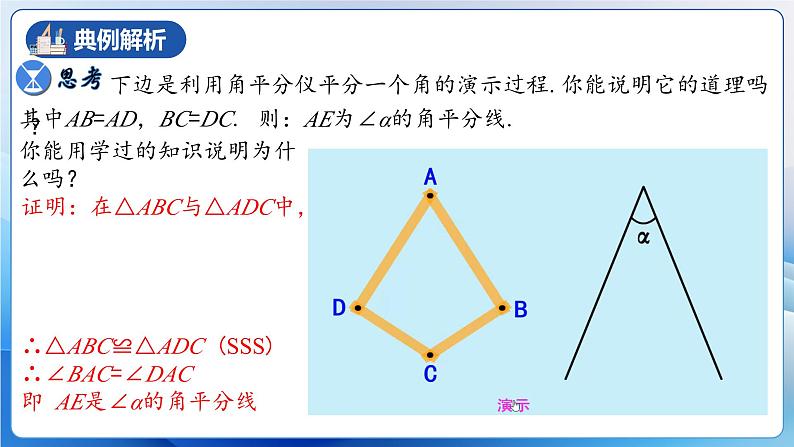
下边是利用角平分仪平分一个角的演示过程.你能说明它的道理吗？
其中AB=AD，BC=DC.
则：AE为∠α的角平分线.
你能用学过的知识说明为什么吗？
证明：在△ABC与△ADC中， ∴△ABC≌△ADC (SSS) ∴∠BAC=∠DAC 即 AE是∠α的角平分线
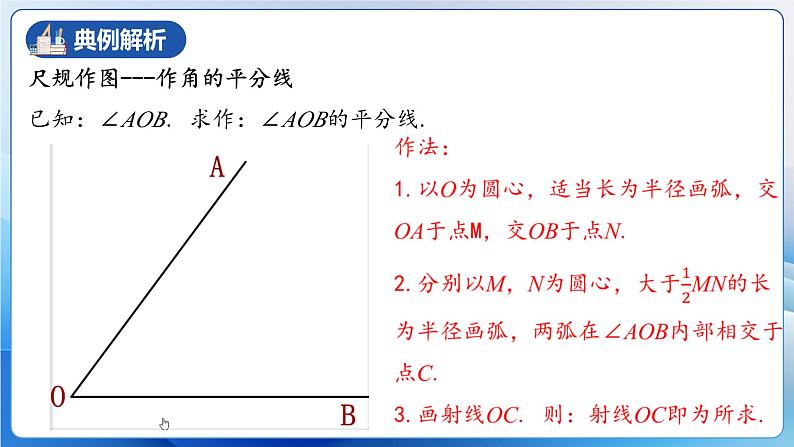
尺规作图---作角的平分线
已知：∠AOB. 求作：∠AOB的平分线.
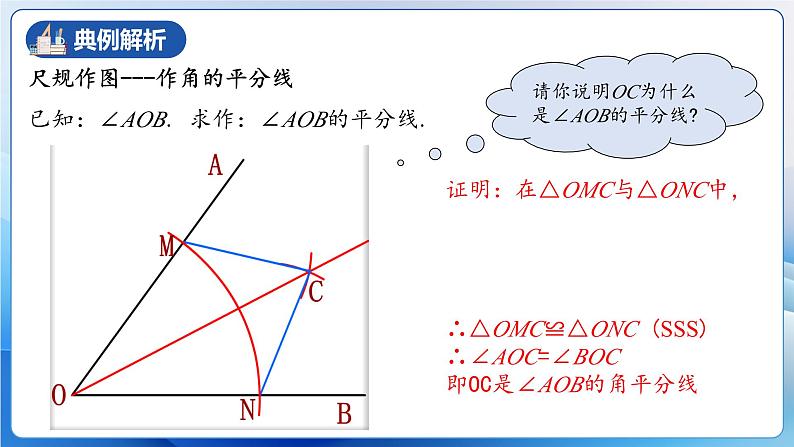
请你说明OC为什么是∠AOB的平分线?
证明：在△OMC与△ONC中， ∴△OMC≌△ONC (SSS) ∴∠AOC=∠BOC 即OC是∠AOB的角平分线
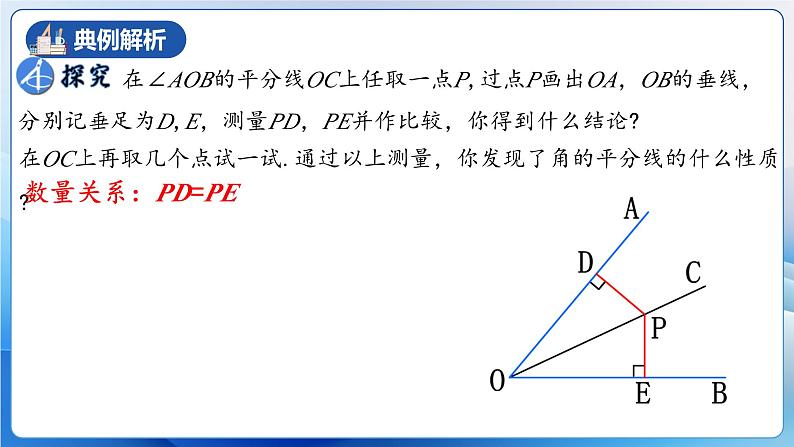
在∠AOB的平分线OC上任取一点P,过点P画出OA，OB的垂线，分别记垂足为D,E，测量PD，PE并作比较，你得到什么结论?
在OC上再取几个点试一试.通过以上测量，你发现了角的平分线的什么性质?
【猜想】角平分线上的点到角的两边的距离相等.
你能利用三角形全等证明这个性质吗？
已知:_________________________________ 求证:_________________________________
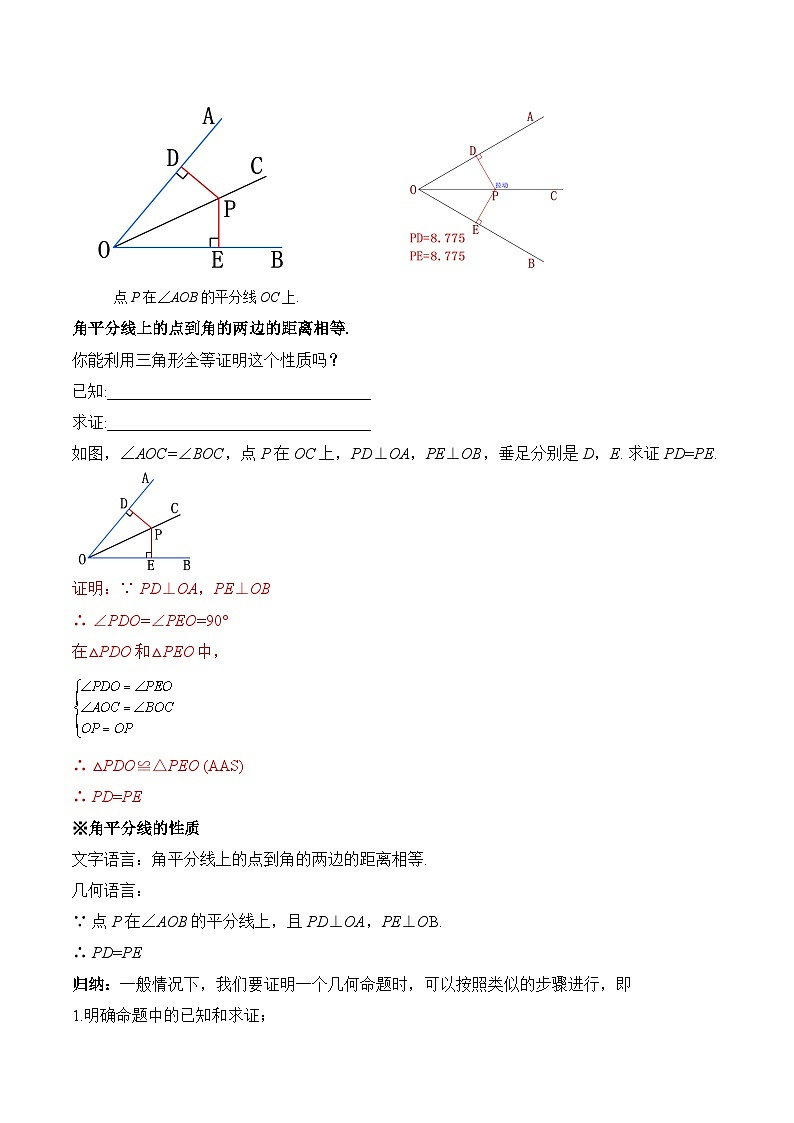
角平分线上的点到角的两边的距离相等.
这个点到这个角两边的距离相等
一个点在一个角的平分线上
如图，∠AOC=∠BOC，点P在OC上，PD⊥OA，PE⊥OB，垂足分别是D，E. 求证PD=PE.
证明：∵PD⊥OA，PE⊥OB ∴∠PDO=∠PEO=90° 在△PDO和△PEO中， ∴△PDO≌△PEO (AAS) ∴PD=PE
文字语言：角平分线上的点到角的两边的距离相等.
∵点P在∠AOB的平分线上，且PD⊥OA，PE⊥OB.∴PD=PE
一般情况下，我们要证明一个几何命题时，可以按照类似的步骤进行，即1.明确命题中的已知和求证；2.根据题意，画出图形，并用数学符号表示已知和求证；3.经过分析，找出由已知推出要证的结论的途径，写出证明过程.
例1.如图，在△ABC中，AD是它的角平分线，且D是BC的中点,DE⊥AB，DF⊥AC，垂足分别是E，F．求证:BE=CF.
如图，D是∠ACG的平分线上的一点．DE⊥AC，DF⊥CG，垂足分别为E，F.求证：CE＝CF.
例2.如图，△ABC中，∠C=90°，AC=BC,AD平分∠CAB交BC于D,问:能否在AB上确定一点E，使△BDE之周长等于AB的长?
解:能在AB上确定一点E,使△BDE的周长等于AB的长.即过点D作DE⊥AB于E，则E点就是所要确定的点.∵AD平分∠CAB，且∠C=90°，DE⊥AB∴DC=DE在Rt△ACD和Rt△AED中,∴Rt△ACD≌Rt△AED(HL)∴AC=AE
∴AC=BC，∴AE=BC∴ C△BDE =BD+DE+BE=BD+DC+BE=BC+BE=AE+BE=AB.
如图，已知AD∥BC，P是∠BAD与∠ABC的平分线的交点，PE⊥AB于E，且PE=3，求AD与BC之间的距离.
解：过点P作MN⊥AD于点M，交BC于点N.∵ AD∥BC，∴ MN⊥BC，MN的长即为AD与BC之间的距离.∵ AP平分∠BAD, PM⊥AD , PE⊥AB，∴ PM=PE.同理， PN=PE.∴ PM= PN= PE=3.∴ MN=6.即AD与BC之间的距离为6.
例3.如图，在△ABC中，D是AB的中点，DE⊥AB，∠ACE+∠BCE=180°，EF⊥AC交AC于F，AC=8，BC=6，则AF=________．
1.如图，∠A=90°，CD平分∠ACB，DE⊥BC于E，且AB=3cm,BD=2cm，则DE=____cm.2.如图，△ABC中，∠C=90°，AD平分∠BAC，AB=5，CD=2，则△ABD的面积为_____.3.如图，△ABC中，∠C=90°，AC=BC，AD平分∠CAB，交BC于点D，DE⊥AB于点E，且AB=6cm，则△DEB的周长为_____cm.
4.如图，在直线MN上求作一点P，使点P到射线OA和OB的距离相等.
5.如图，AD是△ABC的角平分线，DE⊥AB，垂足为E，S△ABC＝7，DE＝2，AB＝4，则AC的长是(　　) A．6 B．5 C．4 D．3
【分析】过点D作DF⊥AC于F，∵AD是△ABC的角平分线，DE⊥AB，∴DF＝DE＝2，∴ ∴AC＝3.
6.如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，且DE＝DG，则∠AED＋∠AGD和是（ ）A．180°B．200°C．210°D．240°
7.如图，OC平分∠AOB，OA=OB，PD⊥AC于D，PE⊥BC于E.求证：PD=PE.