初中数学人教版八年级上册13.1.2 线段的垂直平分线的性质完整版教学作业ppt课件

这是一份初中数学人教版八年级上册13.1.2 线段的垂直平分线的性质完整版教学作业ppt课件，文件包含人教版数学八年级上册1312线段垂直平分线的性质和判定教学课件含动画演示pptx、人教版八年级数学上册1312线段垂直平分线的性质和判定教学设计docx、人教版八年级数学上册1312线段垂直平分线的性质和判定分层作业原卷版docx、人教版八年级数学上册1312线段垂直平分线的性质和判定分层作业解析版docx、人教版八年级数学上册1312线段垂直平分线的性质和判定导学案docx等5份课件配套教学资源，其中PPT共34页， 欢迎下载使用。

情境导入Cntext intrductin
知识精讲Knwledge-based lecture
针对训练Fr training
典例解析Analysis f examples
达标测试Test t meet standards
小结梳理Summary and cmbing
1.理解并掌握线段的垂直平分线的性质和判定方法．(重点）2.会用尺规过一点作已知直线的垂线.3.能够运用线段的垂直平分线的性质和判定解决实际问题．（难点）
如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴.这时，我们也说这个图形关于这条直线(成轴)对称.
像这样，把一个图形沿着某一条直线折叠，如果它能与另一个图形重合，那么就说这两个图形关于这条直线(成轴)对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点.
二、两个图形关于这条直线(成轴)对称
三、垂直平分线经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线.
l⊥AB，垂足为O，且AO=BO，则l是线段AB的垂直平分线.
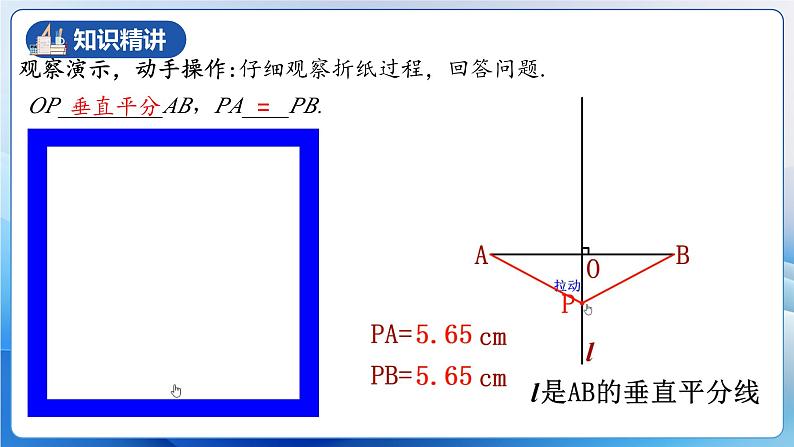
观察演示，动手操作:仔细观察折纸过程，回答问题.
OP_________AB，PA____PB.
线段的垂直平分线的性质：线段垂直平分线上的点与这条线段两个端点的距离相等.
如图，直线l⊥AB，垂足为C，AC=CB，点P在l上.求证PA=PB.
证明：∵ l ⊥AB∴ ∠PCA=∠PCB=90°又∵ AC=BC，PC=PC∴ △PCA≌△PCB (SAS)∴ PA=PB
线段的垂直平分线的性质： 线段垂直平分线上的点与这条线段两个端点的距离相等.
几何符号语言：∵ PC⊥AB，PC平分AB∴ PA=PB
如图，用一根木棒和一根弹性均匀的橡皮筋，做一个简易的“弓”，“箭”通过木棒中央的孔射出去，怎样才能保持射出去的箭的方向与木棒垂直呢？为什么？
如果PA=PB，那么点P是否在线段AB的垂直平分线上呢？
与线段两个端点距离相等的点在这条线段的垂直平分线上.
如图，线段AB，PA=PB. 求证：点P在AB的垂直平分线上.
证法1：过点P作线段AB的垂线PC.∴ ∠PCA=∠PCB=90°又∵ PA=PB，PC=PC∴ Rt△PAC≌Rt△PBC (HL)∴ AC=BC∴ PC是线段AB的垂直平分线∴ 点P在AB的垂直平分线上
证法2：取AB的中点C，过P，C作直线.∴ AC=BC又∵ PA=PB，PC=PC∴ △PAC≌△PBC (SSS)∴ ∠PCA=∠PCB=180°÷2=90°即 PC⊥AB∴ PC是线段AB的垂直平分线∴ 点P在AB的垂直平分线上
线段的垂直平分线的判定：
几何符号语言：∵ PA=PB∴ 点P在AB的垂直平分线上
【性质】线段垂直平分线上的点与这条线段两个端点的距离相等.【判定】与线段两个端点距离相等的点在这条线段的垂直平分线上.
从上面两个结论可以看出：在线段AB的垂直平分线 l 上的点与点A、B的距离都相等；反过来，与A、B的距离相等的点都在直线 l 上，所以直线 l 可以看成与两点A、B的距离相等的所有点的集合.
例1.尺规作图：经过已知直线外一点作这条直线的垂线.
已知：如图，直线AB和AB外一点C.  求作：AB的垂线，使它经过点C.
∵ CD=CE，FD=FE∴ C、F都在DE的垂直平分线上∴ CF垂直平分DE∴ CF⊥AB
想一想，为什么直线CF就是所求作的垂线？
例2.如图，在△ABC中，AB＝AC＝20cm，DE垂直平分AB，垂足为E，交AC于D，若△DBC的周长为35cm，则BC的长为(　　)A.5 cm B.10 cm C.15 cm D.17.5 cm
【分析】∵△DBC的周长为BC＋BD＋CD＝35 cm，又∵DE垂直平分AB，∴AD＝BD，故BC＋AD＋CD＝35 cm.∵AC＝AD＋DC＝20 cm，∴BC＝35－20＝15(cm).故选C.
【点睛】利用线段垂直平分线的性质，实现线段之间的相互转化，从而求出未知线段的长．
1.如图①所示，直线CD是线段AB的垂直平分线，点P为直线CD上的一点，且PA=5，则线段PB的长为（ ）A.6 B.5 C.4 D.3
2.如图②所示，在△ABC中，BC=8cm,边AB的垂直平分线交AB于点D，交边AC于点E, △BCE的周长等于18cm,则AC的长是 .
例3.如图，在△ABC中，AB，AC边的垂直平分线交BC于E，F,垂足分别为M,N，若△ABC周长为18cm,且AB:BC:CA=2:4:3,求△AEF的周长.
解:ME，NF分别是AB，AC的垂直平分线∴AE=BE，AF=CF∴C△AEF=AE+EF+AF=BE+EF+CF=BC设AB=2x，则BC=4x，CA=3x则2x+4x+3x=18解得x=2∴BC=8cm 即△AEF的周长为8cm.
例4.已知：如图，点E是∠AOB的平分线上一点，EC⊥OA,ED⊥OB,垂足分别为C,D，连接CD.求证：OE是CD的垂直平分线.
证明：∵OE平分∠AOB,EC⊥OA,ED⊥OB,∴DE=CE又∵OE=OE，∴Rt△OED≌Rt△OEC. ∴DO=CO.∴OE是CD的垂直平分线.
例5.如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F.求证：(1)FC＝AD；(2)AB＝BC＋AD.
【分析】(1)根据AD∥BC可知∠ADC＝∠ECF，再根据E是CD的中点可得出△ADE≌△FCE，根据全等三角形的性质即可解答；(2)先根据线段垂直平分线的性质得出AB＝BF，再结合（1）即可解答．
证明：(1)∵AD∥BC，∴∠ADC＝∠ECF.∵E是CD的中点，∴DE＝EC.又∵∠AED＝∠CEF，∴△ADE≌△FCE，∴FC＝AD.
(2)∵△ADE≌△FCE，∴AE＝EF，AD＝CF.∵BE⊥AE，∴BE是线段AF的垂直平分线，∴AB＝BF＝BC＋CF.∵AD＝CF，∴AB＝BC＋AD.
2．如图，△ABC中，∠C＝90°，ED垂直平分AB，若AC＝12，EC＝5，且△ACE的周长为30，则BE的长为（     ）A．5 B．10 C．12 D．13
3．如图，在Rt△ABC中，∠B＝90°，ED是AC的垂直平分线，交AC于点D，交BC于点E．已知∠C＝7∠BAE，则∠C的度数为（　 ）A．41° B．42°C．43° D．44°
5．如图，点P为∠AOB内一点，分别作出P点关于OA，OB的对称点P1，P2，连结P1P2交OA于M，交OB于N，若线段P1P2的长为12 cm，则△PMN的周长为_____cm．
6．如图，在△ABC中，AB＝9，BC＝7，AC＝4，直线m是△ABC中BC边的垂直平分线，P是直线上的一动点，△APC周长的最小值为____．
线段的垂直平分的性质和判定
到线段的两个端点距离相等的点在线段的垂直平分线上
线段的垂直平分线上的点到线段的两个端点的距离相等
见垂直平分线，得线段相等
判断一个点是否在线段的垂直平分线上