数学八年级上册13.4课题学习 最短路径问题完美版教学作业ppt课件

这是一份数学八年级上册13.4课题学习 最短路径问题完美版教学作业ppt课件，文件包含人教版数学八年级上册134课题学习最短路径问题教学课件pptx、人教版八年级数学上册134课题学习最短路径问题教学设计docx、人教版八年级数学上册134课题学习最短路径问题分层作业原卷版docx、人教版八年级数学上册134课题学习最短路径问题分层作业解析版docx、人教版八年级数学上册134课题学习最短路径问题导学案docx等5份课件配套教学资源，其中PPT共29页， 欢迎下载使用。

情境导入Cntext intrductin
知识精讲Knwledge-based lecture
针对训练Fr training
典例解析Analysis f examples
达标测试Test t meet standards
小结梳理Summary and cmbing
1.能利用轴对称解决简单的最短路径问题.（难点）2.体会图形的变化在解决最值问题中的作用，感悟转化思想．（重点）
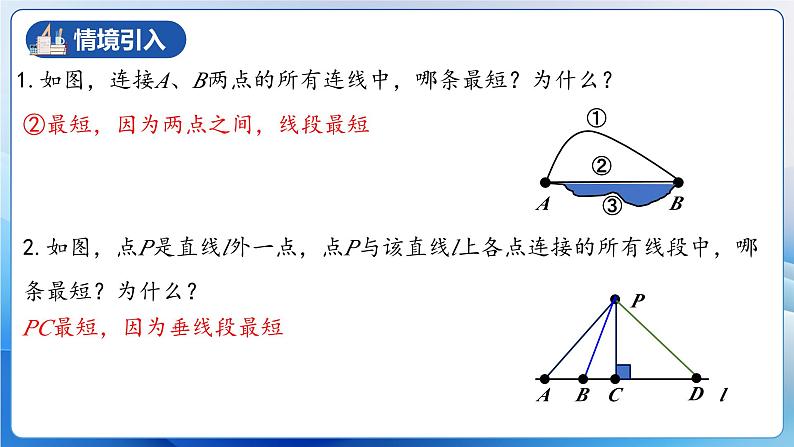
1.如图，连接A、B两点的所有连线中，哪条最短？为什么？
②最短，因为两点之间，线段最短
2.如图，点P是直线l外一点，点P与该直线l上各点连接的所有线段中，哪条最短？为什么？
PC最短，因为垂线段最短
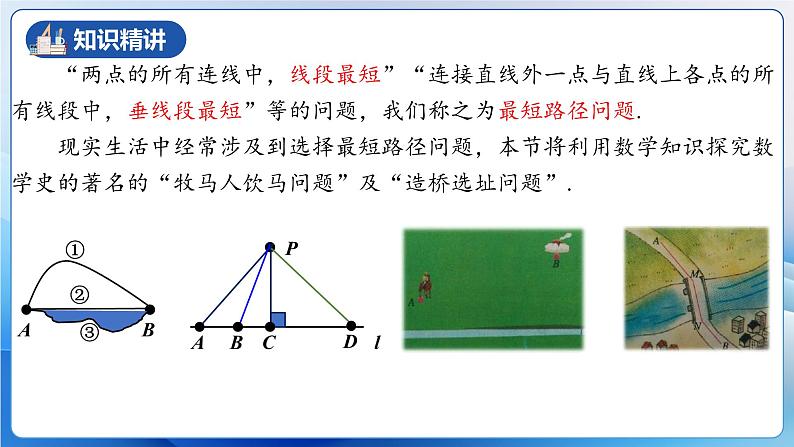
“两点的所有连线中，线段最短”“连接直线外一点与直线上各点的所有线段中，垂线段最短”等的问题，我们称之为最短路径问题. 现实生活中经常涉及到选择最短路径问题，本节将利用数学知识探究数学史的著名的“牧马人饮马问题”及“造桥选址问题”.
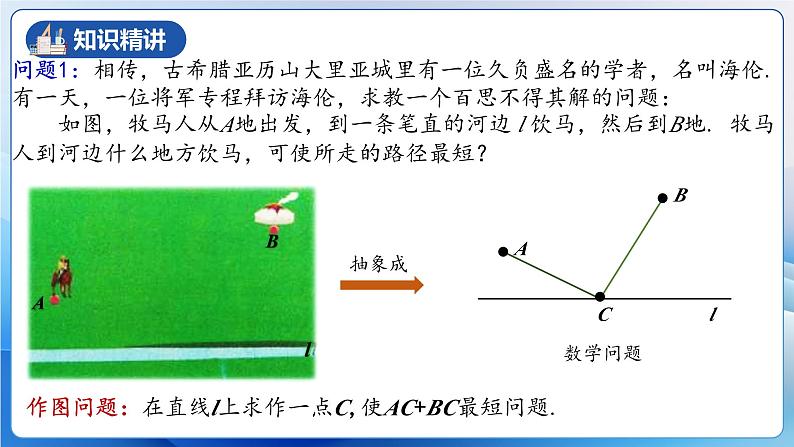
问题1：相传，古希腊亚历山大里亚城里有一位久负盛名的学者，名叫海伦. 有一天，一位将军专程拜访海伦，求教一个百思不得其解的问题： 如图，牧马人从A地出发，到一条笔直的河边 l 饮马，然后到B地. 牧马人到河边什么地方饮马，可使所走的路径最短？
作图问题：在直线l上求作一点C,使AC+BC最短问题.
现在假设点A,B分别是直线l 异侧的两个点，如何在l上找到一个点,使得这个点到点A，点B的距离的和最短？
根据是“两点之间，线段最短”，可知这个交点即为所求.
连接AB,与直线l相交于一点C.
点A，B分别是直线 l 同侧的两个点，如何在 l 上找到一个点，使得这个点到点A、点B的距离的和最短？
思考：1.通过怎样的操作可以把同侧两点转化为异侧两点来解决呢？2.CB 与CB′的长度相等吗？
你能用所学的知识证明AC+BC最短吗？
证明：如图，在直线 l 上任取一点C′(与点C不重合)，连接AC′，BC′，B′C′.由轴对称的性质知，BC=B′C，BC′=B′C′.∴ AC+BC=AC+B′C=AB′ AC′+BC′=AC′+B′C′在△AB′C′中，AB′＜AC′+B′C′∴ AC+BC＜AC′+BC′即AC+BC最短.
例1.如图，已知点D、点E分别是等边三角形ABC中BC、AB边的中点，AD=5，点F是AD边上的动点，则BF+EF的最小值为（　　）A．7.5 B．5 C．4 D．不能确定
解析：△ABC为等边三角形，点D是BC边的中点，即点B与点C关于直线AD对称.∵点F在AD上，故BF=CF.即BF+EF的最小值可转化为求CF+EF的最小值，故连接CE即可，线段CE的长即为BF+EF的最小值.
【点睛】此类求线段和的最小值问题，找准对称点是关键，而后将求线段长的和转化为求某一线段的长，而再根据已知条件求解.
例2.如图，在直角坐标系中，点A，B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A，B，C三点不在同一条直线上，当△ABC的周长最小时点C的坐标是（　　）A．（0，3） B．（0，2） C．（0，1） D．（0，0）
解析：作B点关于y轴对称点B′，连接AB′，交y轴于点C′，此时△ABC的周长最小，然后依据点A与点B′的坐标可得到BE、AE的长，然后证明△B′C′O为等腰直角三角形即可．
【点睛】求三角形周长的最小值，先确定动点所在的直线和固定点，而后作某一固定点关于动点所在直线的对称点，而后将其与另一固定点连线，连线与动点所在直线的交点即为三角形周长最小时动点的位置.
问题2：(造桥选址问题)如图，A和B两地在一条河的两岸，现要河上造一座桥MN. 桥造在何处可使从A到B的路径AMNB最短？(假定河的两岸是平行的直线，桥要与河垂直.)
我们可以把河的两岸看成两条平行线a和b，N为直线b上的一个动点，MN垂直于直线b，交直线a于点M，这样，上面的问题可以转化为下面的问题：当点N在直线b的什么位置时，AM+MN+NB最小？
由于河岸宽度是固定的，因此当AM+NB最小时，AM+MN+NB最小. 这样问题就进一步转化为：当点N在直线b的什么位置时，AM+NB最小？
能否通过图形的变化(轴对称、平移等)，把右图的情况转化为左图的情况？
如图，将AM沿与河岸垂直的方向平移，点M移动到点N，点A移动到点A′，则AA′=MN，AM+NB=A′N+NB. 这样问题就转化为：当点N在直线b的什么位置时，A′N+NB最小？
在连接A′，B两点线中，线段A′B最短. 因此，线段A′B与直线b的交点N的位置即为所求，即在点N处造桥MN，所得路径AMNB是最短的.
你能用所学的知识证明AM+MN+NB最短吗？
为了证明点N的位置即为所求，我们不妨在直线b上另外任意取一点N′，过N′作N′M′⊥a，垂足为M′，连接AM′，A′N′，N′B，证明：AM+MN+NB＜AM′+M′N′+N′B.
证明：如图，由平移的性质可知：AM=A′N，AM′=A′N′，MN=M′N′在△A′BN′中，A′B＜A′N′+N′B∴ A′N+NB＜AM′+N′B∴ AM+NB＜AM′+N′B∴ AM+MN+NB＜AM′+M′N′+N′B
在解决最短路径问题时，我们通常利用轴对称、平移等变化把已知问题转化为容易解决的问题，从而作出最短路径的选择.
例3.如图，荆州古城河在CC′处直角转弯，河宽相同，从A处到B处，须经两座桥：DD ′,EE ′（桥宽不计），设护城河以及两座桥都是东西、南北方向的,怎样架桥可使ADD ′E ′EB的路程最短？
解：作AF⊥CD，且AF=河宽，作BG ⊥CE，且BG=河宽，连接GF，与河岸相交于E ′,D′.作DD′,EE′即为桥.
理由：由平移的性质可知，AD//FD′，AD=FD′.同理，BE=GE′.由两点之间线段最短可知，GF最小.
1.如图，直线l是一条河，P、Q是两个村庄．欲在l上的某处修建一个水泵站,向P、Q两地供水，现有如下四种铺设方案,图中实线表示铺设的管道，则所需管道最短的是( )
2.如图，在△ABC中，AB=AC，AD、CE是△ABC的两条中线，P是AD上一个动点,则下列线段的长度等于BP+EP最小值的是( )A.BC B.CE C.AD D.AC
3.有一条以互相平行的直线a、b为岸的河流，其两侧有村庄A和村庄B，现要在河上建一座桥梁MN(桥与河岸垂直)，使两村庄之间的距离最短，从作图痕迹上来看，正确的是( )
4.如图，在△ABC中，AB=5，BC=4，AC=3.(1)用直尺和圆规作边AB的垂直平分线MN;(2)在直线MN上找一点D，使△ADC的周长最小，并求出△ADC的最小周长.
解:(1)边AB的垂直平分线MN如图所示;
(2)由轴对称确定最短路线问题，点D为MN与BC的交点.∵MN垂直平分AB∴AD=BD∴△ADC的最小周长为:AC+BC=3+4=7
5.甲、乙、丙、丁四人做接力游戏，开始时，甲和乙分别站在∠AOB内的点P与点Q处，丙站在OA上，丁站在OB上.游戏规则:甲将接力棒传给乙，乙将接力棒传给丙，丙将接力棒传给丁，最后丁跑到终点P处.如果甲、乙、丙、丁四人速度相同，试作图求出丙、丁必须站在何处，他们比赛所用时间最短.
解:如图，分别作点P与点Q关于0B、OA的对称点P'、Q'，连接PQ'交OA于点C，交0B于点D，则点C、点D就是丙、丁所站的位置.
6.如图，如果A，B两地之间有两条平行的河流，现要在河上分别建一座桥，且建的桥都是与河岸垂直的．桥建在何处才能使从A到B的路径最短?(保留作图痕迹,不写作法)
解:如图所示，点M、N、P、Q为所求,AMNPQB路径最短.
7.如图，已知∠MON=40°，P为∠MON内一定点，OM上有一点A，ON上有一点B，当△PAB的周长取最小值时，求∠APB的度数.
解:如图，依题意,分别作点P关于ON、OM的对称点P1、P2,连接P1P2交ON于点B，交OM于点A，依次连接A、B、P，此时△PAB的周长为最小值.
由四边形内角和360°可得:∠P1PP2=360°-90°-90°-40°=140°∵BP=BP1，AP=AP2. ∴∠P1=∠BPP1，∠P2=∠APP2∵∠P1+∠P2=180°-140°=40°∴∠BPP1+ ∠APP2=40°∴∠APB=∠P1PP2-∠BPP1-∠APP2=100°