





还剩8页未读,
继续阅读
成套系列资料,整套一键下载
人教版数学八年级上册 第十四章 整式的乘除与因式分解(单元解读)课件
展开
这是一份人教版数学八年级上册 第十四章 整式的乘除与因式分解(单元解读)课件,共16页。
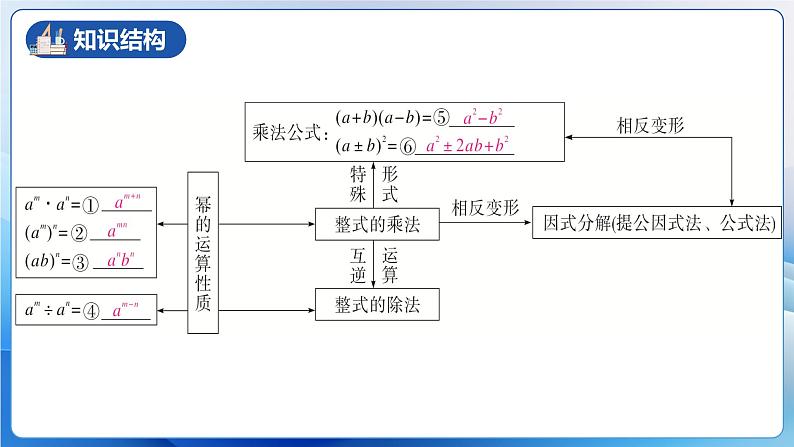
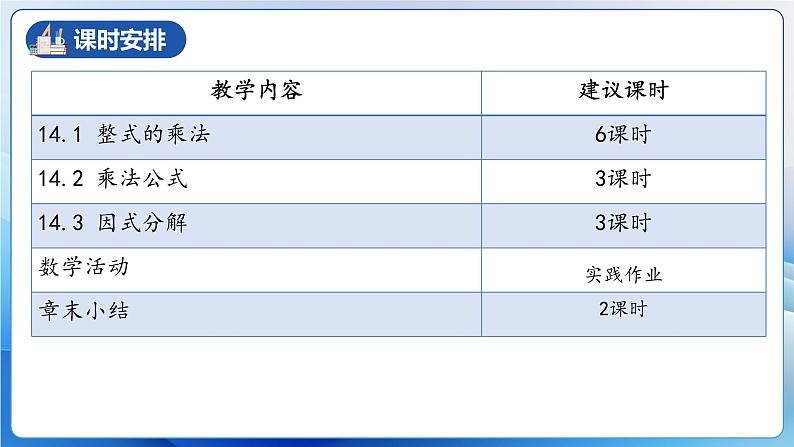
单元解读第十四章 整式的乘除与因式分解课标解读教材内容知识结构课时安排编写意图教学建议1.掌握正整数幂的乘、除运算性质,能用文字和符号语言正确地表述这些性质并能运用它们熟练地进行运算.2.会推导乘法公式(平方差公式和完全平方公式),了解公式的几何意义,能利用公式进行乘法运算.3.掌握整式的加、减、乘、除、乘方的比较简单的混合运算,并能灵活地运用运算律与乘法公式简化运算.4.理解因式分解的意义,并感受因式分解与整式乘法是相反方向的运算,了解因式分解的方法和一般步骤,能熟练运用方法进行多项式的因式分解.1.本章内容建立在已经学习了的有理数运算,列简单的代数式、一次方程及不等式、整式的加减运算等知识的基础上.2.整式的乘法运算和因式分解是基本而重要的代数初步知识,这些知识是以后学习分式和根式运算、函数等知识的基础,在后续的数学学习中具有重要的意义.3.同时,这些知识也是学习物理、化学等学科及其他科学技术不可缺少的数学基础知识.重点:熟练掌握整式乘法的计算和因式分解的解题方法。难点:灵活的应用乘法公式进行运算或进行因式分解。---强调重要思想方法的渗透1.教材渗透了“类比”的思想方法.2.整式乘法法则的教学和整式除法的教学,教科书注意渗透“转化”的思想方法、方程思想和逆向思维的思想方法.3.乘法公式的教学法则渗透了整体思想.例如完全平方公式的常用变形公式.4.本章教材注意了代数与几何之间的联系,体现了“数形结合”的重要思想.---从具体到抽象再到具体的认知过程教材从具体的实际问题出发,归纳出相关的数学概念,或抽象出隐含在具体问题中的数学思想和规律,这是本章的一个突出特点.同时,从多项式乘法到乘法公式体现了从一般到特殊的认知过程.同底数幂相乘、幂的乘方、积的乘方、整式乘法,都是从具体、简单题目的运算出发,最后归纳出运算性质,然后再用归纳得出的结果进一步指导比较复杂的实际问题.这种从具体到抽象,再由抽象到具体的编排方式,可以循序渐进地向学生呈现教学内容,有助于学生的理解和掌握,符合现阶段学生的认知水平.---循序渐进地安排教学内容本章所涉及的教学内容之间不仅具有密切的联系,且具有很强的逻辑关系。因此,在教学中应该注意本章知识之,间的这种逻辑关系,使学生能从整体上把握本章知识.如整式的乘法中,多项式的乘法要利用分配律转化为单项式的乘法,而单项式的乘法要利用交换律和结合律转化为幂的运算,整式的除法与乘法互为逆运算,乘法公式是具有特殊形式的整式乘法问题,因式分解是与整式乘法方向相反的恒等变形.幂的运算是基础,单项式的乘法是关键,学好一般整式乘法的知识是进一步学习本章其他知识的前提.---明确重点、突破难点,把握好教学要求整式的乘法,尤其乘法公式是进一步学 习因式分解、分式及其运算的基础,是第十四章的重点.在整式的乘除中,单项式的乘法是关键,幂的运算是基础.乘法公式的结构特征以及字母的广泛含义学生不容易掌握,运用时容易混淆,因此乘法公式的灵活运用是本章的难点.要突破这一难点, 教学要引导学生分析公式的结构特征,用通俗易懂的语言揭示公式的本质.---重视运算性质和公式的发生和归纳过程的教学整式乘除这部分内容一般都是从特殊到一般,从具体到抽象的过程,学生只有经历了这样的过程,才能更好地理解、记忆公式.---重视新旧知识的联系,引导学生理解运算法则一方面,从本质上来说,有理数的乘法、除法和乘方运算法则与整式乘除运算法则有许多类似之处。在学习式的运算的时候,类比数的运算,可以使学生更好地理解、掌握运算法则.另一方面,本章内容自身之间也有着密切的联系.同底数幂乘法、幂的乘方和积的乘方三种运算,对于理解幂的除法非常有帮助;公式法分解因式完全可以看成乘法公式的逆用.有意识的做好铺垫,可以为后续学习提供方便.---注意纠正学生在运算中的易错点熟练掌握整式乘除和因式分解这两项基本技能,必然需要一定量的练习。然而这种练习并不意味着简单机械的重复.引导学生及时发现并改正自己的计算错误,可以使学生纠正错误认识,正确的理解、运用运算法则,从而提高练习的效率.进行积的乘方运算时,常见的错误有:底数为多个因数时,漏掉某个因式的乘方.进行积的乘方时,系数直接与幂指数相乘,符号易出现错误,如易忽略号:---根据实际情况,适当补充一些内容有一些与本章密切相关的内容,是非常值得加以补充的,如:十字相乘法;分组分解法;配方法.课程结束
单元解读第十四章 整式的乘除与因式分解课标解读教材内容知识结构课时安排编写意图教学建议1.掌握正整数幂的乘、除运算性质,能用文字和符号语言正确地表述这些性质并能运用它们熟练地进行运算.2.会推导乘法公式(平方差公式和完全平方公式),了解公式的几何意义,能利用公式进行乘法运算.3.掌握整式的加、减、乘、除、乘方的比较简单的混合运算,并能灵活地运用运算律与乘法公式简化运算.4.理解因式分解的意义,并感受因式分解与整式乘法是相反方向的运算,了解因式分解的方法和一般步骤,能熟练运用方法进行多项式的因式分解.1.本章内容建立在已经学习了的有理数运算,列简单的代数式、一次方程及不等式、整式的加减运算等知识的基础上.2.整式的乘法运算和因式分解是基本而重要的代数初步知识,这些知识是以后学习分式和根式运算、函数等知识的基础,在后续的数学学习中具有重要的意义.3.同时,这些知识也是学习物理、化学等学科及其他科学技术不可缺少的数学基础知识.重点:熟练掌握整式乘法的计算和因式分解的解题方法。难点:灵活的应用乘法公式进行运算或进行因式分解。---强调重要思想方法的渗透1.教材渗透了“类比”的思想方法.2.整式乘法法则的教学和整式除法的教学,教科书注意渗透“转化”的思想方法、方程思想和逆向思维的思想方法.3.乘法公式的教学法则渗透了整体思想.例如完全平方公式的常用变形公式.4.本章教材注意了代数与几何之间的联系,体现了“数形结合”的重要思想.---从具体到抽象再到具体的认知过程教材从具体的实际问题出发,归纳出相关的数学概念,或抽象出隐含在具体问题中的数学思想和规律,这是本章的一个突出特点.同时,从多项式乘法到乘法公式体现了从一般到特殊的认知过程.同底数幂相乘、幂的乘方、积的乘方、整式乘法,都是从具体、简单题目的运算出发,最后归纳出运算性质,然后再用归纳得出的结果进一步指导比较复杂的实际问题.这种从具体到抽象,再由抽象到具体的编排方式,可以循序渐进地向学生呈现教学内容,有助于学生的理解和掌握,符合现阶段学生的认知水平.---循序渐进地安排教学内容本章所涉及的教学内容之间不仅具有密切的联系,且具有很强的逻辑关系。因此,在教学中应该注意本章知识之,间的这种逻辑关系,使学生能从整体上把握本章知识.如整式的乘法中,多项式的乘法要利用分配律转化为单项式的乘法,而单项式的乘法要利用交换律和结合律转化为幂的运算,整式的除法与乘法互为逆运算,乘法公式是具有特殊形式的整式乘法问题,因式分解是与整式乘法方向相反的恒等变形.幂的运算是基础,单项式的乘法是关键,学好一般整式乘法的知识是进一步学习本章其他知识的前提.---明确重点、突破难点,把握好教学要求整式的乘法,尤其乘法公式是进一步学 习因式分解、分式及其运算的基础,是第十四章的重点.在整式的乘除中,单项式的乘法是关键,幂的运算是基础.乘法公式的结构特征以及字母的广泛含义学生不容易掌握,运用时容易混淆,因此乘法公式的灵活运用是本章的难点.要突破这一难点, 教学要引导学生分析公式的结构特征,用通俗易懂的语言揭示公式的本质.---重视运算性质和公式的发生和归纳过程的教学整式乘除这部分内容一般都是从特殊到一般,从具体到抽象的过程,学生只有经历了这样的过程,才能更好地理解、记忆公式.---重视新旧知识的联系,引导学生理解运算法则一方面,从本质上来说,有理数的乘法、除法和乘方运算法则与整式乘除运算法则有许多类似之处。在学习式的运算的时候,类比数的运算,可以使学生更好地理解、掌握运算法则.另一方面,本章内容自身之间也有着密切的联系.同底数幂乘法、幂的乘方和积的乘方三种运算,对于理解幂的除法非常有帮助;公式法分解因式完全可以看成乘法公式的逆用.有意识的做好铺垫,可以为后续学习提供方便.---注意纠正学生在运算中的易错点熟练掌握整式乘除和因式分解这两项基本技能,必然需要一定量的练习。然而这种练习并不意味着简单机械的重复.引导学生及时发现并改正自己的计算错误,可以使学生纠正错误认识,正确的理解、运用运算法则,从而提高练习的效率.进行积的乘方运算时,常见的错误有:底数为多个因数时,漏掉某个因式的乘方.进行积的乘方时,系数直接与幂指数相乘,符号易出现错误,如易忽略号:---根据实际情况,适当补充一些内容有一些与本章密切相关的内容,是非常值得加以补充的,如:十字相乘法;分组分解法;配方法.课程结束
相关资料
更多











