（12）图形的相似——2024年中考数学真题专项汇编

这是一份（12）图形的相似——2024年中考数学真题专项汇编，共25页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
一、单选题
1．[2024年重庆中考真题]若两个相似三角形的相似比为，则这两个三角形面积的比是( )
A.B.C.D.
2．[2024年内蒙古赤峰中考真题]如图，中，，.将绕点A顺时针旋转得到，点与点B是对应点，点与点C是对应点.若点恰好落在BC边上，下列结论：①点B在旋转过程中经过的路径长是；②；③；④.其中正确的结论是( )
A.①②③④B.①②③C.①③④D.②④
3．[2024年湖南中考真题]如图，在中，点D，E分别为边，的中点.下列结论中，错误的是( )
A.B.C.D.
4．[2024年山东枣庄中考真题]如图，点为的对角线上一点，，，连接并延长至点F，使得，连接，则为( )
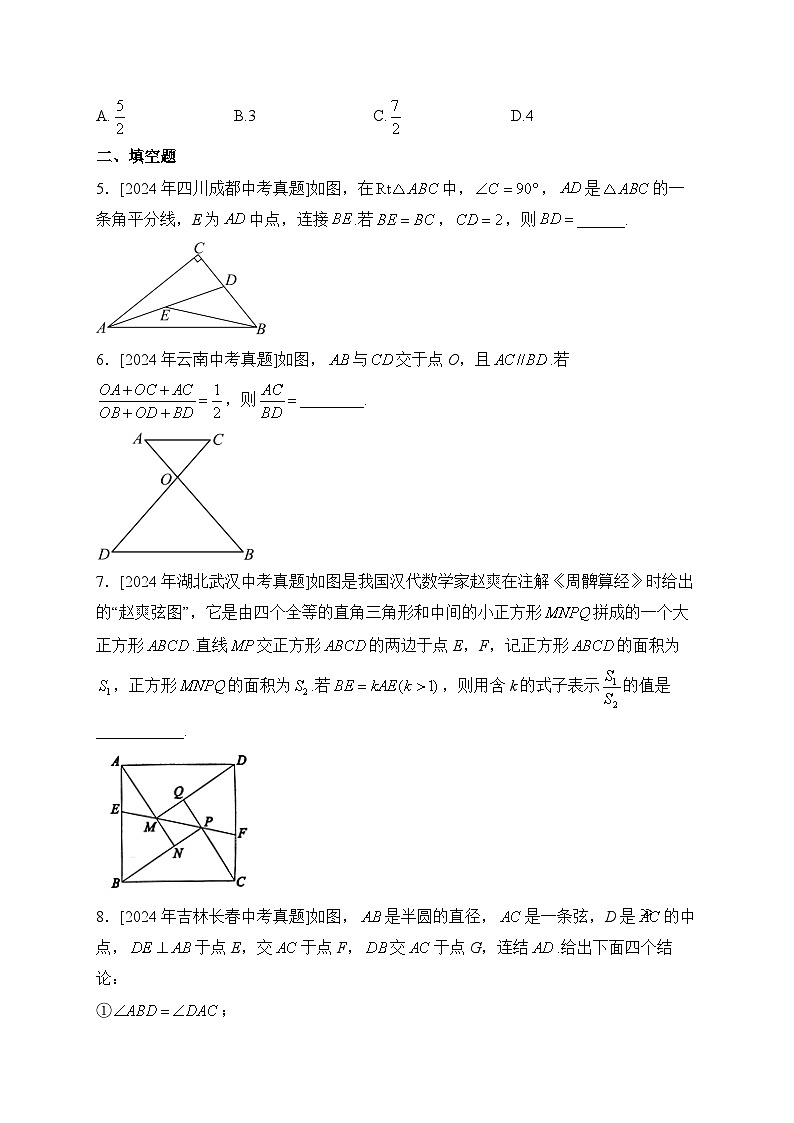
A.B.3C.D.4
二、填空题
5．[2024年四川成都中考真题]如图，在中，，是的一条角平分线，E为中点，连接.若，，则______.
6．[2024年云南中考真题]如图，与交于点O，且.若，则________.
7．[2024年湖北武汉中考真题]如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.直线交正方形的两边于点E，F，记正方形的面积为，正方形的面积为.若，则用含k的式子表示的值是___________.
8．[2024年吉林长春中考真题]如图，是半圆的直径，是一条弦，D是的中点，于点E，交于点F，交于点G，连结.给出下面四个结论：
①；
②；
③当，时，；
④当，时，的面积是.
上述结论中，正确结论的序号有_________.
9．[2024年吉林中考真题]如图，正方形的对角线，相交于点O，点E是的中点，点F是上一点.连接.若，则的值为______.
三、解答题
10．[2024年河北中考真题]如图，的面积为2，为边上的中线，点A，，，是线段的五等分点，点A，，是线段的四等分点，点A是线段的中点.
（1）的面积为______；
（2）的面积为______.
11．[2024年湖北中考真题]如图，矩形中，E，F分别在，上，将四边形沿翻折，使E的对称点P落在上，F的对称点为G，交于H.
（1）求证：.
（2）若P为中点，且，，求长.
（3）连接，若P为中点，H为中点，探究与大小关系并说明理由.
12．[2024年贵州中考真题]综合与探究：如图，，点P在的平分线上，于点A.
（1）【操作判断】
如图①，过点P作于点C，根据题意在图①中画出，图中的度数为______度；
（2）【问题探究】
如图②，点M在线段上，连接，过点P作交射线于点N，求证：；
（3）【拓展延伸】
点M在射线上，连接，过点P作交射线于点N，射线与射线相交于点F，若，求的值.
13．[2024年四川广元中考真题]数学实验，能增加学习数学的乐趣，还能经历知识“再创造”的过程，更是培养动手能力，创新能力的一种手段.小强在学习《相似》一章中对“直角三角形斜边上作高”这一基本图形（如图1）产生了如下问题，请同学们帮他解决.
在中，点D为边上一点，连接.
（1）初步探究
如图2，若，求证：；
（2）尝试应用
如图3，在（1）的条件下，若点D为中点，，求的长；
（3）创新提升
如图4，点E为中点，连接，若，，，求的长.
14．[2024年四川南充中考真题]如图，正方形边长为，点E为对角线上一点，，点P在边上以的速度由点A向点B运动，同时点Q在边上以的速度由点C向点B运动，设运动时间为t秒（）.
（1）求证：.
（2）当是直角三角形时，求t的值.
（3）连接，当时，求的面积.
15．[2024年内蒙古赤峰中考真题]数学课上，老师给出以下条件，请同学们经过小组讨论，提出探究问题.如图1，在中，，点D是上的一个动点，过点D作于点E，延长交延长线于点F.
请你解决下面各组提出的问题：
（1）求证：；
（2）探究与的关系；
某小组探究发现，当时，；当时，.
请你继续探究：
①当时，直接写出的值；
②当时，猜想的值（用含m，n的式子表示），并证明；
（3）拓展应用：在图1中，过点F作，垂足为点P，连接，得到图2，当点D运动到使时，若，直接写出的值（用含m，n的式子表示）.
参考答案
1．答案：D
解析：两个相似三角形的相似比为，这两个三角形面积的比是，故选：D.
2．答案：A
解析：，，
，，
由旋转的性质得，，，，，
，
，
，
，
由旋转的性质得，
，
①点B在旋转过程中经过的路径长是；①说法正确；
②，；②说法正确；
③，
，
；③说法正确；
④，，
，
.④说法正确；
综上，①②③④都是正确的，
故选：A.
3．答案：D
解析：点D，E分别为边，的中点，
，，故A、C正确；
，
，故B正确；
，
，
，故D错误；
故选：D.
4．答案：B
解析：延长和，交于G点，
四边形是平行四边形，
，即，
，
，，
，
，
又，，
，
，，
，
，
，
，
，
.
故选：B.
5．答案：
解析：连接，过E作于F，设，，
，E为中点，
，又，
，，，
，，
，
，则，又，
，
，，
，
则；
是的一条角平分线，
，又，
，
，
，则，
，即，
解得（负值已舍去），
故答案为：.
6．答案：
解析：，
，
，
故答案为：.
7．答案：
解析：作交于点G，不妨设，设，
四边形是正方形，
，
，
，
在和中，，，
，
，
，
，
，
，
由题意可知，，
，
，
，
，
，
正方形的面积，
正方形的面积，
，
，
，
.
8．答案：①②③
解析：如图：连接，
D是的中点，
，
，即①正确；
是直径，
，
，
，
，
，
，
，，
，
，
，
，
，即②正确；
在和，
，
，
，即，
，即，
，
，
，即③正确；
如图：假设半圆的圆心为O，连接，，，
，，D是的中点，
，
，
，是等边三角形，
，即是菱形，
，
，
，即，解得：，
，
，
，即④错误.
故答案为：①②③.
9．答案：
解析：正方形的对角线，相交于点O，
，，
点E是的中点，
，
，
，
，
，即，
故答案为：.
10．答案：（1）1
（2）7
解析：（1）连接、、、、，
的面积为2，为边上的中线，
，
点A，，，是线段的五等分点，
，
点A，，是线段的四等分点，
，
点A是线段的中点，
，
在和中，
，
，
，，
的面积为1，
故答案为：1；
（2）在和中，
，
，
，，
，
，
、、三点共线，
，
，
，
，，
，
在和中，
，，
，
，
，
，
，
，
的面积为7，
故答案为：7.
11．答案：（1）见详解
（2）
（3）
解析：（1）如图：
四边形是矩形，，，E，F分别在，上，将四边形沿翻折，使A的对称点P落在上，，，，；
（2）如图：
四边形是矩形，，，，P为中点，，设，，在中，，即，解得，，，，，，解得，，；
（3）如图：延长，交于一点M，连接，E，F分别在，上，将四边形沿翻折，使A的对称点P落在上，，直线，，，，，是等腰三角形，，P为中点，设，，H为中点，，，，，
，，，在中，，，，在中，，，，，，，.
12．答案：（1）画图见解析，90
（2）见解析
（3）或
解析：（1）如图，即为所求，
，，，
四边形是矩形，
，
故答案为：90；
（2）证明：过P作于C，
由（1）知：四边形是矩形，
点P在的平分线上，，，
，
矩形是正方形，
，，
，
，
又，，
，
，
；
（3）①当M在线段上时，如图，延长、相交于点G，
由（2）知，
设，则，，
，
，，
，
，
，，
，
，
，
，
；
②当M在的延长线上时，如图，过P作于C，并延长交于G
由（2）知：四边形是正方形，
，，，
，
，
又，，
，
，
，
，，
，
，
，即，
，
，
，
，
，
；
综上，的值为或.
13．答案：（1）证明见解析
（2）
（3）
解析：
14．答案：（1）见解析
（2）秒或2秒
（3）
解析：（1）证明：四边形是正方形，
.
，，，
，
.
（2）过点E作于点M，过点E作于点N.
由题意知，
，
，
，
，，
由已知，
，，，，，.
，即，
，即，
，即.
①当时，有.
即，整理得.
解得，（不合题意，舍去）.
②当时，有.
即，整理得，解得.
③当时，有.
即，整理得，该方程无实数解.
综上所述，当是直角三角形时，t的值为秒或2秒.
（3）过点A作，交的延长线于点F，连接交于点G.
，，
.
又，
，
.
，
，
，
，
，
，
，
，
，
即，
是等腰直角三角形.
，
.
15．答案：（1）见解析
（2）①②，证明见解析
（3）
解析：（1）证明：，
，
，
，
，，且，
，
；
（2）①当时，；当时，，
总结规律得：是的2倍，
当时，；
②当时，猜想，
证明：作于点G，
，
，
，
，
，
由（1）知，又，
，即，
；
（3），理由如下：
过点D作，
，，
，
由（2）知，当时，，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
由（1）知，
.