（新知衔接）专题07 分数的混合运算（三）（三大考点讲练+难度分层练）（含答案）2024年新六年级数学暑假衔接讲义（北师大版）

这是一份（新知衔接）专题07 分数的混合运算（三）（三大考点讲练+难度分层练）（含答案）2024年新六年级数学暑假衔接讲义（北师大版），文件包含新知衔接专题07分数的混合运算三新知讲练+高频易错点+三大考点讲练+难度分层练原卷版2024年新六年级数学暑假衔接讲义北师大版docx、新知衔接专题07分数的混合运算三新知讲练+高频易错点+三大考点讲练+难度分层练解析版2024年新六年级数学暑假衔接讲义北师大版docx等2份试卷配套教学资源，其中试卷共41页， 欢迎下载使用。
（新知讲练+高频易错点+三考点讲练+难度分层练）
编者的话：
同学你好，这份讲义包含：
①新课讲授知识精讲：从复习到预习，典例精讲，理解知识点运用方法，逐步掌握新课内容！结合变式训练提升知识点应用能力，自学效果也很好！
②高频易错点拨精讲：对常考题型易错点内容指点，强化学生对知识点的理解和运用，查漏补缺，给出解决方案，提高学生的解题谨慎度、细心度！
③考点精讲练：对本节内容进行细致划分，逐个学习新知，学生理解更透彻，结合变式演练，举一反三训练，掌握知识点的运用技巧！
④【基础夯实+冲刺拔高】真题练：结合近两年常考真题，易错题，经典题型等进一步巩固所学内容，提升解题能力，熟悉考点考察题型，达到事半功倍！
TOC \ "1-3" \h \u \l "_Tc2785" 考点01：已知比一个数多或少几分之几是多少，求这个数 PAGEREF _Tc2785 \h 6
\l "_Tc25083" 考点02：已知一部分量占总量的几分之几及另一部分量，求总量 PAGEREF _Tc25083 \h 9
\l "_Tc9479" 考点03：用转化法或倒推法解决稍复杂的分数应用题 PAGEREF _Tc9479 \h 11
\l "_Tc24005" 基础达标练 PAGEREF _Tc24005 \h 15
\l "_Tc23830" 能力拔高练 PAGEREF _Tc23830 \h 22
1.用方程表达分数混合运算问题中的等量关系。
2.解决相应的实际问题，发展分析和解决问题的能力。
3.构建数学模型，教育学生节约用水，培养勤俭节约的好习惯。
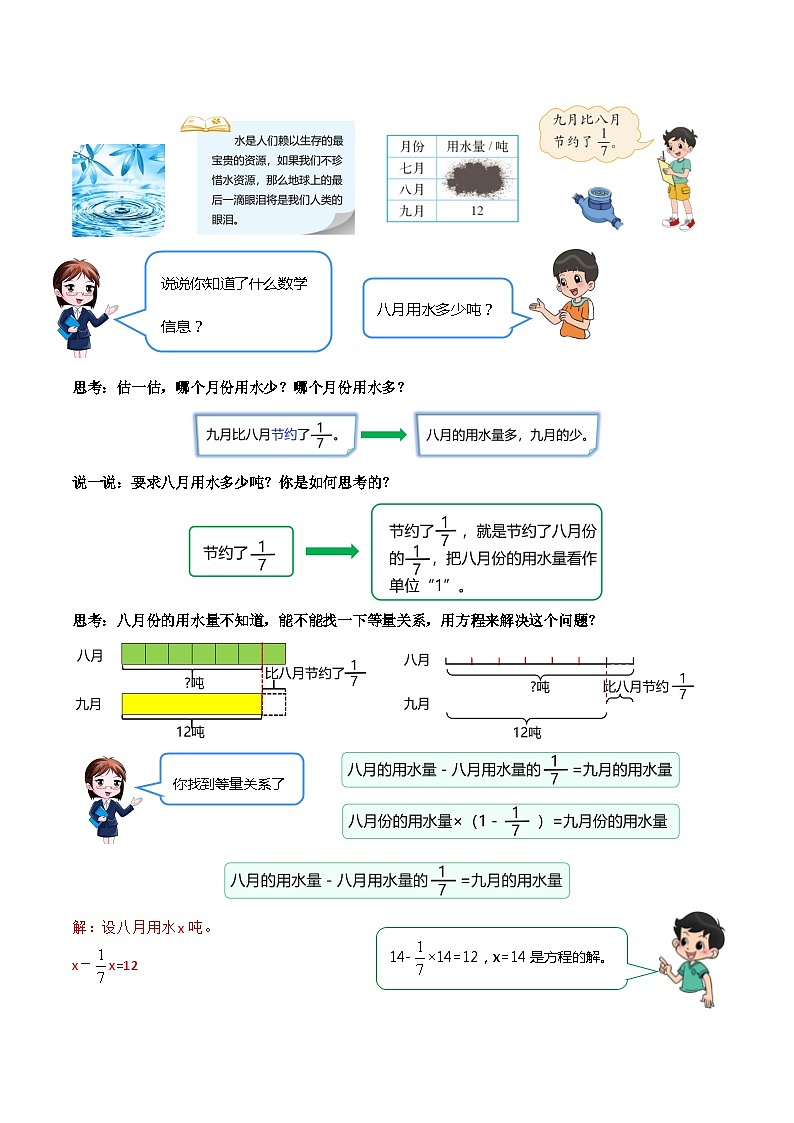
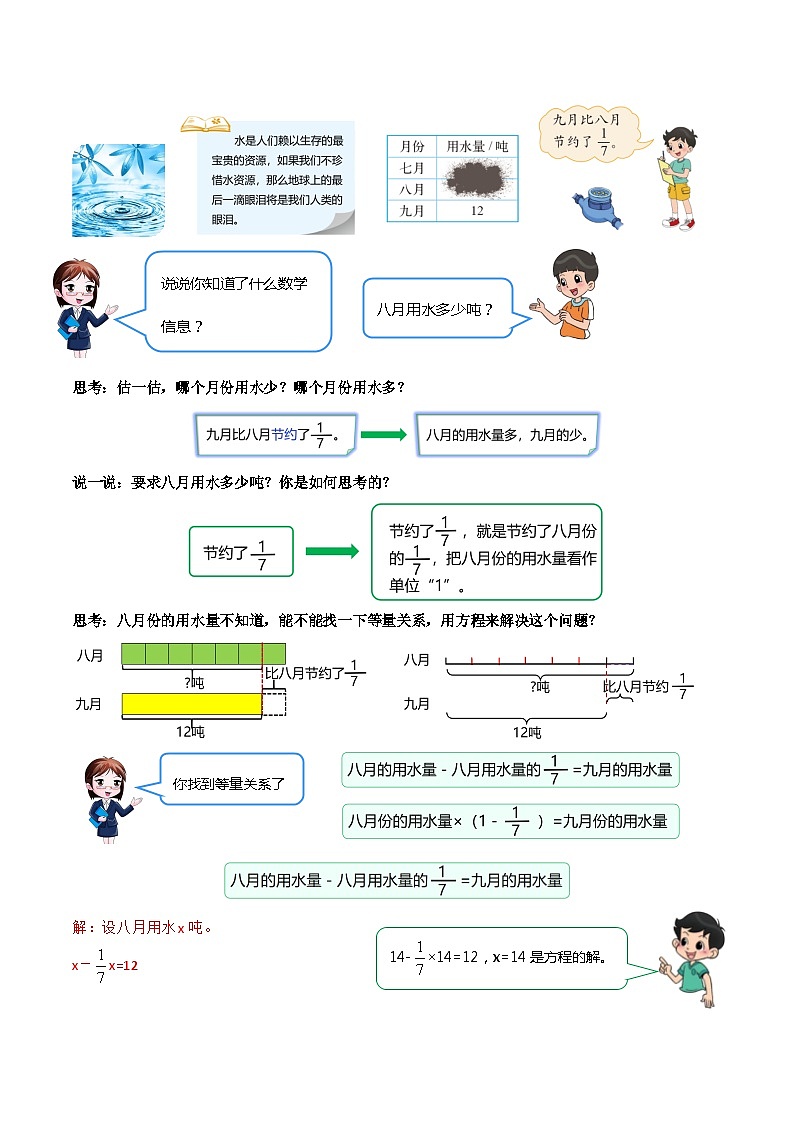
八月用水多少吨？

说说你知道了什么数学信息？
思考：估一估，哪个月份用水少？哪个月份用水多？
说一说：要求八月用水多少吨？你是如何思考的？
思考：八月份的用水量不知道，能不能找一下等量关系，用方程来解决这个问题？

你找到等量关系了吗？

14-×14=12，x=14是方程的解。
解：设八月用水x吨。
x－x=12
x=12
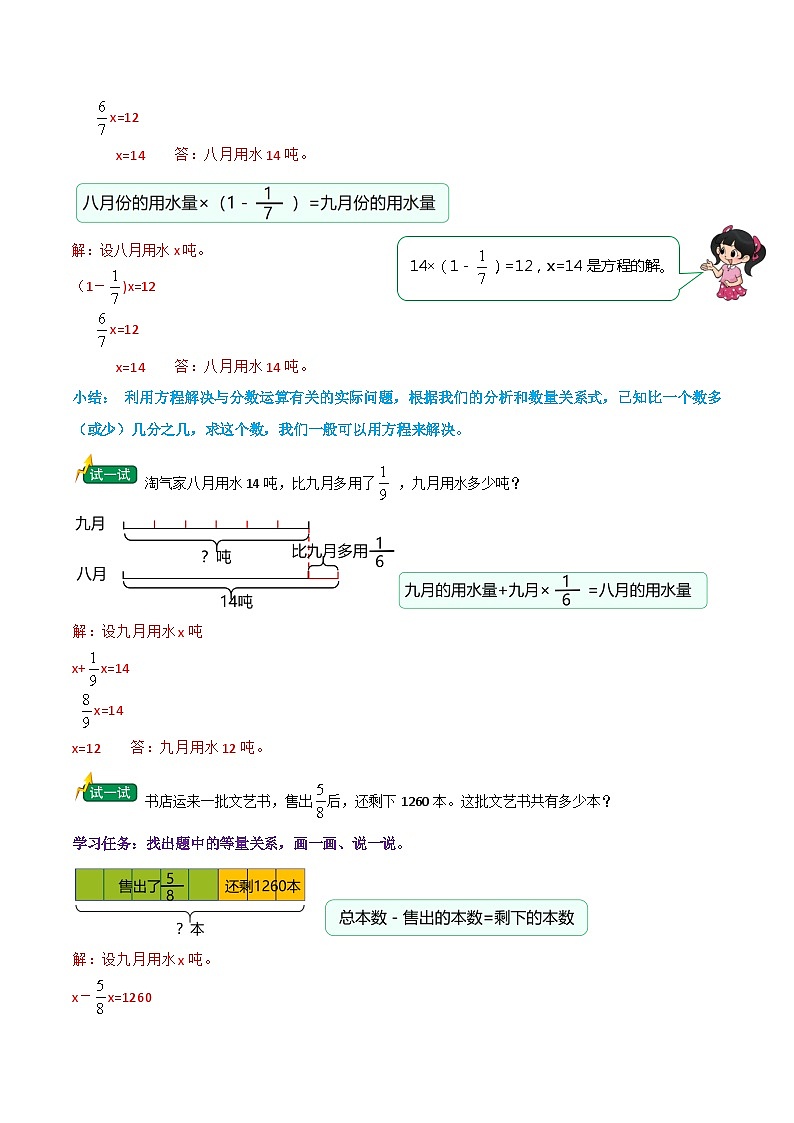
x=14 答：八月用水14吨。
14×（1－）=12，x=14是方程的解。
解：设八月用水x吨。
（1－)x=12
x=12
x=14 答：八月用水14吨。
小结： 利用方程解决与分数运算有关的实际问题，根据我们的分析和数量关系式，已知比一个数多（或少）几分之几，求这个数，我们一般可以用方程来解决。
淘气家八月用水14吨，比九月多用了 ，九月用水多少吨？
解：设九月用水x吨
x+x=14
x=14
x=12 答：九月用水12吨。
书店运来一批文艺书，售出后，还剩下1260本。这批文艺书共有多少本？
学习任务：找出题中的等量关系，画一画、说一说。

解：设九月用水x吨。
x－x=1260
x=1260
x=3360 答：这批文艺书共有3360本。
解：设九月用水x吨。
（1－）x=1260
x=1260
x=3360 答：这批文艺书共有3360本。
知识点01：已知比一个数多或少几分之几是多少，求这个数
这个知识点主要考察的是对分数增减运算的逆向应用。题目通常会给出某个数比另一个数多或少几分之几，然后给出具体的结果，要求求出原来的数。
解题步骤：
理解题意：明确题目中给出的“多几分之几”或“少几分之几”以及具体的结果。
设立未知数：设原来的数为x。
建立方程：根据题目描述，建立包含x的方程。
解方程：解出x的值。
知识点02：已知一部分量占总量的几分之几及另一部分量，求总量
这个知识点主要考察的是对分数比例的应用。题目会给出总量中的一部分量所占的比例以及另一部分量的具体数值，要求求出总量。
解题步骤：
理解题意：明确题目中给出的比例和具体数值。
设立未知数：设总量为x。
建立方程：根据题目描述，利用比例关系建立包含x的方程。
解方程：解出x的值。
知识点03：运用转化法或倒推法解决稍复杂的分数应用题
在解决稍复杂的分数应用题时，转化法和倒推法是非常有效的解题技巧。
转化法：
转化法是将题目中的复杂条件或问题转化为简单、易于理解的形式。例如，可以将分数转化为小数，或将复杂的比例关系转化为简单的等式。
倒推法：
倒推法是从问题的结果出发，逆向推导出问题的初始条件或已知条件。这种方法在解决逆向思维问题时特别有效。
易错知识点01：已知比一个数多或少几分之几是多少，求这个数
易错点：
理解题意不清：学生可能没有正确理解题目中的“多几分之几”或“少几分之几”的含义，导致解题方向错误。
设立方程错误：在设立未知数时，学生可能会将未知数设立在错误的位置，导致方程建立不正确。
计算错误：在解方程的过程中，学生可能会出现计算错误，导致最终答案不正确。
解题策略：
仔细审题，明确题目中的“多几分之几”或“少几分之几”是指哪个数与哪个数之间的关系。
设立未知数，通常设要求的数为未知数。
根据题目描述，建立包含未知数的方程。
解方程，得出未知数的值。
易错知识点02：已知一部分量占总量的几分之几及另一部分量求总量
易错点：
比例关系理解不清：学生可能没有正确理解题目中给出的比例关系，导致解题方向错误。
计算错误：在根据比例关系计算总量时，学生可能会出现计算错误。
解题策略：
仔细审题，明确题目中给出的比例关系以及另一部分量的具体数值。
设立未知数，通常设总量为未知数。
根据比例关系，建立包含未知数的方程。
解方程，得出未知数的值，即总量。
易错知识点03：运用转化法或倒推法解决稍复杂的分数应用题
易错点：
转化方法不当：学生可能没有找到合适的转化方法，导致问题复杂化。
倒推步骤错误：在使用倒推法时，学生可能会出现步骤错误，导致最终答案不正确。
解题策略：
转化法：
仔细审题，找出题目中的关键信息。
尝试将题目中的复杂条件或问题转化为简单、易于理解的形式。
转化后，按照常规方法解题。
倒推法：
从问题的结果出发，逆向推导出问题的初始条件或已知条件。
逐步倒推，每一步都要确保正确无误。
得出最终答案后，检查是否符合题目要求。
考点01：已知比一个数多或少几分之几是多少，求这个数
【典例精讲】（23-24六年级上·广东湛江·期末）学校图书馆有故事书420本，______，科技书有多少本？为了解决这个问题，乐乐补充一条信息后，设科技书有x本，列出的方程是“”，乐乐补充的信息是（ ）。
A．故事书比科技书少B．故事书比科技书多
C．科技书比故事书少D．科技书比故事书多
【答案】A
【思路点拨】A．如果补充“故事书比科技书少”，科技书本数是单位“1”，故事书是科技书的（1－），设科技书有x本，根据科技书本数×故事书对应分率＝故事书本数，列方程；
B．如果补充“故事书比科技书多”， 科技书本数是单位“1”，故事书是科技书的（1＋），设科技书有x本，根据科技书本数×故事书对应分率＝故事书本数，列方程；
C．如果补充“科技书比故事书少”，故事书本数是单位“1”，科技书是故事书的（1－），故事书本数×科技书对应分率＝科技书本数；
D．如果补充“科技书比故事书多”， 故事书本数是单位“1”，科技书是故事书的（1＋），故事书本数×科技书对应分率＝科技书本数。
【规范解答】A．补充“故事书比科技书少”，设科技书有x本，可以列出方程：；
B．补充“故事书比科技书多”，设科技书有x本，可以列出方程：；
C．补充“科技书比故事书少”，可以直接列式：420×（1－）；
D．补充“科技书比故事书多”，可以直接列式：420×（1＋）。
乐乐补充的信息是故事书比科技书少。
故答案为：A
【变式演练01】（23-24六年级上·辽宁·课后作业）说一说图意，再列式计算。
【答案】说一说见详解；20支
【思路点拨】从图中可知，钢笔有25支，钢笔比中性笔的支数多，把中性笔的支数看作单位“1”，则钢笔的支数是中性笔的（1＋），单位“1”未知，用钢笔的支数除以（1＋），即可求出中性笔的支数。
【规范解答】图意：钢笔有25支，钢笔比中性笔的支数多，中性笔有多少支？
25÷（1＋）
＝25÷
＝25×
＝20（支）
即中性笔有20支。
【变式演练02】（23-24六年级上·陕西商洛·期末）元旦假期，奇奇和爸爸妈妈一起去姥姥家。请你根据下面的信息帮奇奇解决问题。
（1）如果今年还坐火车去姥姥家，那么需要用（ ）小时。
（2）如果今年坐高铁去姥姥家，那么需要用多长时间？
【答案】（1）20
（2）8小时
【思路点拨】（1）去年乘火车用了24小时，今年火车比去年提前的时间到达。把去年乘火车用的时间看作单位“1”，则今年乘火车用的时间是去年的（1－），根据“求一个数的几分之几是多少，用乘法计算”，用24乘（1－），即可求出今年坐火车需要的时间。
（2）现在火车比高铁多花的时间，把坐高铁花的时间看作单位“1”，则现在坐火车需要的时间是高铁时间的（1＋），根据“已知一个数的几分之几是多少，求这个数，用除法计算”，用求得的现在坐火车需要的时间除以（1＋），即可求出坐高铁需要的时间。
【规范解答】（1）24×（1－）
＝24×
＝20（小时）
则如果今年还坐火车去姥姥家，需要用20小时。
（2）20÷（1＋）
＝20÷
＝20×
＝8（小时）
答：如果今年坐高铁去姥姥家，需要8小时。
【变式演练03】（23-24六年级上·广东湛江·期末）“面人”是一种民间传统的手工艺品。手工课上淘气捏一个唐僧用了250克面粉，捏一个唐僧需要的面粉比捏一个猪八戒少。捏一个猪八戒需要多少克面粉？
【答案】300克
【思路点拨】把捏一个猪八戒需要的面粉看作单位“1”，捏一个唐僧需要的面粉是捏一个猪八戒的（1－），根据分数除法的意义，用250÷（1－）即可求出捏一个猪八戒需要多少克面粉。
【规范解答】250÷（1－）
＝250÷
＝250×
＝300（克）
答：捏一个猪八戒需要300克面粉。
考点02：已知一部分量占总量的几分之几及另一部分量，求总量
【典例精讲】（22-23六年级上·山西忻州·期末）一堆货物，运走了，还剩30吨，这堆货物原来有 吨。
【答案】180
【思路点拨】将原来吨数看作单位“1”，运走了，还剩（1－），剩下的吨数÷对应分率＝原来的吨数，据此列式计算。
【规范解答】30÷（1－）
＝30÷
＝30×6
＝180（吨）
这堆货物原来有180吨。
【变式演练01】（23-24六年级上·福建莆田·期末）为了丰富学生的课余生活，逸夫小学开展了学生课后社团活动。六年级原来参加围棋社的女生人数是男生人数的，后来又增加了10名女生，这时男生人数是女生的。原来参加围棋社的女生有多少名？
【答案】10名
【思路点拨】男生人数没变，将男生人数看作单位“1”，后来又增加了10名女生，这时男生人数是女生的，则女生人数是男生人数的，增加的女生人数对应分率是（－），增加的女生人数÷对应分率＝男生人数，男生人数×原来女生对应分率＝原来女生人数，据此列式解答。
【规范解答】10÷（－）
＝10÷
＝10×
＝15（名）
15×＝10（名）
答：原来参加围棋社的女生有10名。
【变式演练02】（23-24六年级上·河南南阳·期中）为美化校园环境，学校粉刷宣传长廓，已刷了，还剩50平方米没有刷，宣传长廓的总面积是多少平方米？
【答案】300平方米
【思路点拨】由题意可知，已刷了是将整个宣传长廊需要粉刷的面积看作单位“1”，没有刷的面积占总面积的（），已知还剩50平方米没有刷，求单位“1”的量，总面积等于没有刷的面积除以没有刷的部分所占的分率，据此解答。
【规范解答】
（平方米）
答：宣传长廓的总面积是300平方米。
【变式演练03】（23-24六年级上·河南周口·期末）食堂新买来一批大米，第一周吃了总数的，后来又吃了总数的，现在还剩130kg，食堂新买来的这批大米有（ ）kg。
A．360B．290C．450D．440
【答案】C
【思路点拨】第一周吃了总数的，后来又吃了总数的，则剩下的大米所占的分率为1－－，将大米总数量看作单位“1”，根据分数除法的意义，已知剩下大米所占的分率，也知道剩下大米的具体数值，求单位“1”用除法，即用剩下大米的具体数值除以其所占的分率，即可求出这批大米的总数量。
【规范解答】由分析可得：
130÷（1－－）
＝130÷（－）
＝130÷（－）
＝130÷
＝130×
＝450（kg）
食堂新买来的这批大米有450kg。
故答案为：C
考点03：用转化法或倒推法解决稍复杂的分数应用题
【典例精讲】三个袋中各装一些球，现从甲袋中取出的小球放入乙袋，然后乙袋中取出现在的放入丙袋，最后再从丙袋中取出现在的放入甲袋，那么各袋中的球都是18个，原来甲袋中有（ ）个球。
A．21B．24C．27D．40
【答案】B
【思路点拨】各袋中的球数都是18个为突破口，已知从丙袋中取出放入甲袋后，丙袋球数是18个，则丙袋把球拿走之前是18÷（1－）＝20（个），则可知从丙袋中放入甲袋的球的是20×＝2（个）；
因为现在各袋中的球都是18个，则甲袋放入2个球之前是18－2＝16（个）球，又知先从甲袋中取出了的小球放入乙袋，即从甲袋中拿走后是16个球，那么甲袋中原有球的个数是16÷（1－）＝24（个）球。
【规范解答】18÷（1－）
＝18÷
＝18×
＝20（个）
18－20×
＝18－2
＝16（个）
16÷（1－）
＝16÷
＝16×
＝24（个）
则原来甲袋中有球24个。
故答案为：B
【考点评析】本题重在区分好拿走前和放入后的单位“1”，是不同的，还要灵活应用倒推法。
【变式演练01】（21-22六年级上·山东德州·期末）有一根绳子，第一次剪下一半又1米，第二次剪下剩下的一半又1米，还剩1米。这根绳子原来有多长？（ ）
A．7米B．8米C．9米D．10米
【答案】D
【思路点拨】假设原来有x米，根据题意可列方程为：（x÷2－1）÷2－1＝1，据此解出方程即可。
【规范解答】解：设绳子原来有x米。
（x÷2－1）÷2－1＝1
（x÷2－1）÷2－1＋1＝1＋1
（x÷2－1）÷2＝2
（x÷2－1）÷2×2＝2×2
x÷2－1＝4
x÷2－1＋1＝4＋1
x÷2＝5
x÷2×2＝5×2
x＝10
绳子原来有10米。
故答案为：D
【考点评析】本题可用列方程解决问题，也可用逆推法解决问题。
【变式演练02】（21-22六年级上·湖南永州·期中）修一段路，第一天修了300米，第二天修了余下的一半少200米，第三天修了余下的多100米，这时还余下500米没有修。这段路全长多少米？
【答案】4700米
【思路点拨】先把第二天修完后余下的长度看作单位“1”，则（500＋100）米占它的（1－），单位“1”未知，用除法求出第二天修完后余下的长度；
再把第一天修完后余下的长度看作单位“1”，则第二天修完后余下长度减去200米的长度占它的（1－），单位“1”未知，用除法求出第一天修完后余下的长度；
最后用第一天修的长度加上第一天修完后余下的长度，即是这段路的全长。
【规范解答】第二天修完后余下的长度：
（500＋100）÷（1－）
＝600÷
＝600×4
＝2400（米）
第一天修完后余下的长度：
（2400－200）÷（1－）
＝2200÷
＝2200×2
＝4400（米）
全长：4400＋300＝4700（米）
答：这段路全长4700米。
【考点评析】本题考查分数除法的应用，利用“倒推法”解题，找出单位“1”，区分单位“1”的不同，单位“1”未知，根据分数除法的意义解答。
【变式演练03】（21-22六年级上·湖北武汉·期末）风采大赛之后，老师拿了一箱奖品发给获奖的同学们。将其中的发给一等奖的同学，剩下的发给二等奖的同学，一、二等奖发完后剩下的发给三等奖的同学，这时箱子里还剩下15份奖品，问箱子里原来有多少份奖品？
【答案】45份
【思路点拨】先把一、二等奖发完后剩下奖品的份数看作单位“1”，那么箱子里还剩下15份奖品占它的，单位“1”未知，用除法计算，求出一、二等奖发完后剩下奖品的份数；
再把一等奖发完后剩下奖品的份数看作单位“1”，那么一、二等奖发完后剩下奖品的份数占它的，单位“1”未知，用除法计算，求出一等奖发完后剩下奖品的份数；
最后把箱子里原来有奖品的总数看作单位“1”，那么一等奖发完后剩下奖品的份数占它的，单位“1”未知，用除法计算，求出箱子里原来有奖品的总数。
【规范解答】一、二等奖发完后剩下：
（份）
一等奖发完后剩下：
（份）
原来的奖品总数：
（份）
答：箱子里原来有45份奖品。
【考点评析】本题考查复杂的分数除法的应用，找出单位“1”，单位“1”未知，根据分数除法的意义列式计算；注意三个单位“1”的不同，采用倒推法解答。
基础达标练
1．（2024六上·慈溪期末）修一段100米长的路，甲单独修10天完成，乙单独修15天完成。现在甲、乙合作6天，下列说法正确的是（ ）。
A．还没有完成B．正好完成
C．已经提前完成D．无法确定
【答案】B
【规范解答】解：（100÷10＋100÷15）×6
=×6
=100（米）
故答案为：B。
【思路点拨】工作总量÷甲独修用的时间=甲的工作效率，工作总量÷乙独修用的时间=乙的工作效率，（工作总量÷甲独修用的时间+工作总量÷乙独修用的时间）×合作时间=甲乙合修的工作总量，最后比较合修的工作总量与要修的路长进行比较即可解答。
2．（2024六上·天台期末）甲商品的单价是360元，乙商品的单价与甲商品单价的关系如图所示。关于甲乙两件商品单价之间的关系，下列说法正确的是（ ）。
A．乙和甲的单价比是6：5B．乙的单价是
C．乙的单价比甲少D．甲的单价比乙多
【答案】D
【规范解答】解：A项中，乙和甲的单价比是5：6；
B项中， 乙的单（6-5）÷6=价是360×；
C项中，（6-5）÷6=，所以乙的单价比甲少；
D项中，（6-5）÷5=，所以甲的单价比乙多。
故答案为：D。
【思路点拨】甲商品是6份，乙商品是5份，所以乙和甲的单价比是5：6；
乙的单价=甲的单价×乙是甲的几分之几；
乙的单价比甲少几分之几=（甲的单价占的份数-乙的单价占的份数）÷甲的单价占的份数；
甲的单价比乙多几分之几=（甲的单价占的份数-乙的单价占的份数）÷乙的单价占的份数。
3．（2024六上·印江期末） 加工400个零件，师傅单独加工要8小时才能完成，徒弟单独加工要10小时才能完成。如果列式为“”，要解决的问题是（ ）。
A．师徒合作1小时完成这批零件的几分之几
B．师徒合作1小时加工多少个零件
C．师徒合作完成400个零件需要多少小时
【答案】C
【规范解答】解：(+)表示师傅和徒弟两人合作的工作效率，1表示工作总量，工作总量÷工作效率=工作时间，因此，1÷(+)表示师徒合作完成400个零件需要多少小时；
故答案为：C。
【思路点拨】把工作总量看做单位“1”，因此，表示师傅的工作效率，表示徒弟的工作效率，据此解答。
4．（2024六上·象山期末）一项工程，甲队单独做需20天完成，乙队单独做需30天完成。甲、乙的工作效率之比是 。甲、乙两队合做， 天可以完成这项工程的。
【答案】3：2；8
【规范解答】解：第一问：：=3：2；
第二问：
÷（+）
=÷
=8（天）。
故答案为：3：2；8。
【思路点拨】第一问：把这项工程看作“1”，用分子是1的分数表示出两队的工作效率，写出工作效率的比并化成最简整数比；
第二问：用需要完成的工作量除以两队的工作效率和即可求出完成的天数。
5．（2024六上·丹江口期末）在通常情况下，物体都具有热胀冷缩的特性。但是水是一种特殊的液体，温度在4℃ 以上时，遵循热胀冷缩规律。4℃以下时，水会热缩冷胀。温度低于0℃，水会凝固成冰，体积会明显变大。所以在生活中，我们不能把瓶装饮料和啤酒放到冰箱冷冻，否则会冻裂。
（1）夏季常温下1 L水，放入冰箱后水温变成了3℃，这是水的体积 1 L。（填大于、等于、小于）
（2）体积相等的冰和水，冰的质量比水的质量少。现在有一块重9kg的冰，如果一桶水的体积和这块冰的体积相同，这桶水重 kg。
【答案】（1）大于
（2）10
【规范解答】解：（1）这时水的体积大于1L；
（2）9÷（1-）
=9÷
=10（kg）。
故答案为：（1）大于；（2）10。
【思路点拨】（1）因为放入冰箱后水温变成了3℃，小于4℃，水会热缩冷胀，那么这时水的体积大于1L；
（2）这桶水的重量=等体积的冰的重量÷（1-等体积的冰的质量比水的质量少几分之几），据此作答即可。
6．（2024六上·泽普期末）图书馆共有科技书和故事书630本，其中科技书的本数是故事书的，科技书有 本，故事书有 本。
【答案】140；490
【规范解答】解：故事书的本数看做7份，科技书的本数是7×=2；
630÷（7+2）
=630÷9
=70（本）
70×2=140（本）
70×7=490（本）
故答案为：140；490。
【思路点拨】科技书和故事书的总本数÷总份数=一份的本数，一份的本数×2=科技书的本数，一份的本数×7=故事书的本数。
7．（2024六上·义乌期末）递等式计算，能简便的要简便计算。


【答案】解：
=×48+×48-×48
=12+8-4
=16
=÷[×2]
=÷
=
=58×+×43-
=×（58+43-1）
=×100
=80
=7.8×+2.2×
=（7.8+2.2）×
=10×
=2.5
=×
=
=×15×17+×15×17
=17+15
=32
【思路点拨】（1）（3）（4）（6）运用乘法分配律计算；
（2）先算加法，再算乘法，最后算除法；
（5）从左到右依次计算。
8．（2024六上·平湖期末）张师傅带了一些钱去购买办公桌椅。这些钱如果全部用来购买桌子，可以买20张；如果全部用来购买椅子，可以买30把。这些钱可以买多少套办公桌椅？（一张桌子和一把椅子是1套）
【答案】解：1÷(+)
=1÷
=12(套)
答：这些钱可以买12套办公桌椅。
【思路点拨】把总钱数看作单位“1”，那么一张桌子的钱数就占总钱数的，一把椅子的钱数就占总钱数的；一套桌椅的钱数就占总钱数的(+)，用单位“1”除以一套桌椅的分率即可解答。
9．（2024六上·郓城期末）C919大型客机是中国首款完全按照最新国际适航标准研制的单通道大型干线客机，具有中国完全的自主知识产权。C919大型客机的翼展约36m， 翼展比机身的长度短。C919大型客机的机身的长度约多少米？
【答案】解：36÷（1-）
=36÷
=39（米）
答：C919大型客机的机身的长度约39
【思路点拨】C919大型客机的机身的长度=C919大型客机的翼展的长度÷（1-翼展比机身的长度短几分之几），据此代入数值作答即可。
10．（2024六上·黄岩期末）“一年好景君须记，最是橙黄橘绿时”，果园里橘子大丰收了！今年王奶奶还尝试了“直播带货”，销量大增，一共卖出了3500千克，其中通过直播卖出的橘子数量是线下的。线上直播卖出了多少千克?
【答案】解：3500÷（1＋）×
=3500÷×
=2000×
=1500（千克）
答：线上直播卖出了1500千克。
【思路点拨】线上直播卖出的质量=卖出的总质量÷（1＋线上直播占的分率）×线上直播占的分率。
11．（2024六上·确山期末）两位师傅给一间房贴地砖。张师傅单独做5天可以贴完，李师傅单独做4天可以贴完，他们合做2天后，还剩下8平方米没有贴。这间房有多少平方米?
【答案】解：（+）×2
=×2
=
8÷（1-）
=8÷
=80（平方米）
答：这间房有80平方米。
【思路点拨】他们合做2天，完成这间房几分之几=张师傅和李师傅每天一共贴几分之几×2，他们合做2天后还剩这间房的几分之几=1-他们合做2天完成这间房的几分之几，所以所以这间房的面积=还剩的面积÷他们合做2天后还剩这间房的几分之几。
12．（2024六上·凉州期末）一项工程，甲队单独做10天完成，乙队的工作效率是甲队的。如果甲、乙两队合做，几天可以完成这项工程的？
【答案】解：×=
÷（+）
=÷
=5（天）
答：5天可以完成这项工程的。
【思路点拨】乙队的工作效率=甲队的工作效率×乙队的工作效率是甲队的几分之几，把这项工程看成单位“1”，那么完成这项工程的需要的天数=÷甲队和乙队的工作效率之和，据此代入数值作答即可。
13．（2024六上·亭湖期末）为迎接新年，实验小学六(3)班布置教室，买了一个大灯笼和12个小灯笼，一共花费112元.已知一个小灯笼是一个大灯笼单价的。小灯笼和大灯笼的单价各是多少元?
【答案】解：1÷=4（个）
112÷（4+12）
=112÷16
＝7（元）
7÷=28（元）
答：小灯笼的单价是7元，大灯笼的单价是28元。
【思路点拨】一个大灯笼相当于小灯笼的个数=1÷一个小灯笼是一个大灯笼单价的几分之几，所以小灯笼的单价=一个大灯笼和12个小灯笼一共的钱数÷（12+4），大灯笼的单价=小灯笼的单价÷乙个小灯笼是一个大灯笼单价的几分之几，据此代入数值作答即可。
能力拔高练
14．（2023六上·郯城月考）今年的产量比去年多，今年的产量相当于去年的（ ）。
A．B．C．D．
【答案】C
【规范解答】解：1＋=
÷1=。
故答案为：C。
【思路点拨】把去年的产量看作单位“1”，今年的产量=1＋=，今年的产量相当于去年的分率=今年的产量÷去年的产量。
15．（2023六上·龙岗期中）一瓶牛奶，如果喝掉后，连瓶重800g；如果喝掉一半后，连瓶重700g。则瓶子重（ ）g
A．300B．400C．500D．600
【答案】B
【规范解答】解：（800-700）÷（-）
=100÷
=600（克）
700-600×
=700-300
=400（克）。
故答案为：B。
【思路点拨】瓶子的质量=喝掉一半后连瓶的总质量-总质量×；其中，总质量=（喝掉后连瓶的质量-喝掉一半后连瓶的质量）÷（-）。
16．学校一次课外活动，缺勤人数是出勤人数的10％，后来又有2人因病请假，这时缺勤人数是出勤人数的 ，这个学校课外活动小组共有（ ）
A．99人B．90人C．100人
【答案】A
【规范解答】解：10＋1=11
8＋1=9
2÷（-）
=2÷
=99（人）。
故答案为：A。
【思路点拨】学校组织这次课外活动的总人数是一定的，原来缺勤人数是出勤人数的10%（即），也就是缺勤人数是出勤人数的，后来又有2人因病请假，这时缺勤人数是出勤人数的 ，这时缺勤人数占总人数的，那么这个学校课外活动小组共有的人数=2÷（-）。
17．（2024六上·沐川期末）在一个减法算式里，被减数、减数和差的和是140，减数是差的。这个减法算式的差是 ，减数是 。
【答案】42；28
【规范解答】解：（1+）++1=，140÷=42，所以减法算式的差是42；42×=28，所以减数是28。
故答案为：42；28。
【思路点拨】把差看成单位“1”，减数则是，所以被减数是1+=，所以差=被减数、减数和差的和÷（++1），减数=差×减数是差的几分之几。
18．（2023六上·如皋月考）六（1）班的同学上体育课时整齐的排列成两队，乐乐数了数，排在他前面的人数是总人数的，排在他后面的人数是总人数的。乐乐这一队一共有 人，从前往后数，乐乐排在第 位。
【答案】15；7
【规范解答】解：1÷（1--）
=1÷（-）
=1÷
=15（人）
15×＋1
=6＋1
=7（位）。
故答案为：15；7。
【思路点拨】乐乐这一队的总人数=乐乐1人÷（1-乐乐前面人数占的分率-乐乐后面人数占的分率）；乐乐排的位次数=乐乐这一队的总人数×乐乐前面人数占的分率＋1人。
19．（2023六上·汉川期中）印度也像中国一样有着灿烂的文化，古代印度有这样一道有趣的数学题：有一群蜜蜂，其中落在牡丹花上，落在栀子花上，这两者的差的三倍，飞向月季花，最后剩下一只小蜜蜂在芳香的茉莉花和玉兰花之间飞来飞去，共有 只蜜蜂。
【答案】15
【规范解答】解：（-）×3
=×3
=
1---
=--
=-
=
1÷=15（只）。
故答案为：15。
【思路点拨】共有蜜蜂的只数=最后剩下蜜蜂的只数÷最后一只蜜蜂占的分率；其中，最后一只蜜蜂占的分率=1-落在牡丹花上的分率-落在栀子花上的分率-飞向月季花的分率。
20．（2020六上·武侯期末）用递等式计算。
（1）（3.5+ ）÷ -1.5
（2）[ +（ -1.21× ）]÷40%
【答案】（1）（3.5+ ）÷ -1.5
=（+）×-1.5
=（+）×-1.5
=×-1.5
=-1.5
=0
（2）[ +（ -1.21×）]÷40%
= [21.15+（5.4 -0.55）]÷0.4
= [21.15+4.85]÷0.4
=26÷0.4
=65
【思路点拨】（1）将带分数化为假分数，再根据分数四则混合运算，先算括号里的，再算括号外的，能够约分的要约分；（2）将带分数化为小数进行计算，再根据小数四则混合运算，先算小括号里的，再算中括号里的，最后算括号外的，能约分的要约分。
21．（2024·一外）在某大坝截流时，用载重卡车将一堆石料运到围堰龙口，第一次运了这堆石料的少2万方，第二次运了剩下的多3万方，此时还剩下12万方未运，则这堆石料共有多少万方？
【答案】解：（12＋3）÷（1-）
=15÷
=30（万方）
（30-2）÷（1-）
=28÷
=42（万方）
答：这堆石料共有42万方。
【思路点拨】用逆推法：先把余下的质量看作单位“1”，假设第二天运来剩下的，则还剩下余下的1-=，还剩12＋3=15万方，则余下15÷=30万方；进而把这堆石料看作单位“1”，第一次运了这堆石料的少2万方，然后用除法求出这堆石料共有多少万方。
22．（2024六上·英山期末）小明看一本书，第一次看的比全书的少7页，第二次看的比全书的多5页，还剩下267页没看。这本书一共有多少页？
【答案】解：（267-7+5）÷（1--）
=265÷
=300（页）
答：这本书一共有300页。
【思路点拨】这本书一共的页数=（还剩下的页数-7页＋5页）÷（1-第一次看的分率-第二次看的分率）。
23．（2024六上·莲湖期末）快递公司配送一批加急件，已配送的件数与剩下的件数比是3：4，如果再配送80件，剩下的比已经配送的少 ，这批加急件一共有多少件？
【答案】解：3÷（3＋4）
=3÷7
=
1-=
1÷（1＋）
=1÷
=
80÷（-）
=80÷
=280（件）
答：这批加急件一共有280件。
【思路点拨】这批加急件一共的件数=再配送的件数÷所占的分率，其中，再配送的件数所占的分率=-原来配送的占的分率。
24．（·渝北）有一条线段AB，以端点A为起点量出全长的 在线段上做记号M，以端点B为起点量出全长的 在线段上做记号N．如果M和N之间的长度是14cm，那么整条线段AB的长度是多少？
【答案】解：1﹣ ＝
1﹣ ＝
14÷（1﹣ ﹣ ）
＝14÷
＝30（厘米）
答：整条线段AB的长度是30厘米。
【思路点拨】此题可以借助画图的方法，关键是找准14厘米线段的对应分率，把线段AB的全长看作单位“1”，已知AM占，则MB占1-=，已知BN占，则NA占1-=，那么线段MN占全长的1--，最后用线段MN的长度÷线段MN占全长的分率=线段AB的长度，据此列式解答。
25．（2023六上·玉环期中）一件工程，如果甲队单独做要15天完成，乙队2天可以完成这件工程的，甲队单独做5天后，甲乙合作还需要几天完成？
【答案】解：÷2=
（1-×5）÷（＋）
=（1-）÷
=÷
=4（天）
答：甲乙合作还需要4天完成。
【思路点拨】甲、乙合作完成还需要的天数=（1-甲队的工作效率×甲单独做的天数）÷（甲队的工作效率＋乙队的工作效率）。