






还剩14页未读,
继续阅读
成套系列资料,整套一键下载
第五章 一元一次方程章末小结 课件 2024-2025学年人教版七年级数学上册
展开
这是一份第五章 一元一次方程章末小结 课件 2024-2025学年人教版七年级数学上册,共22页。
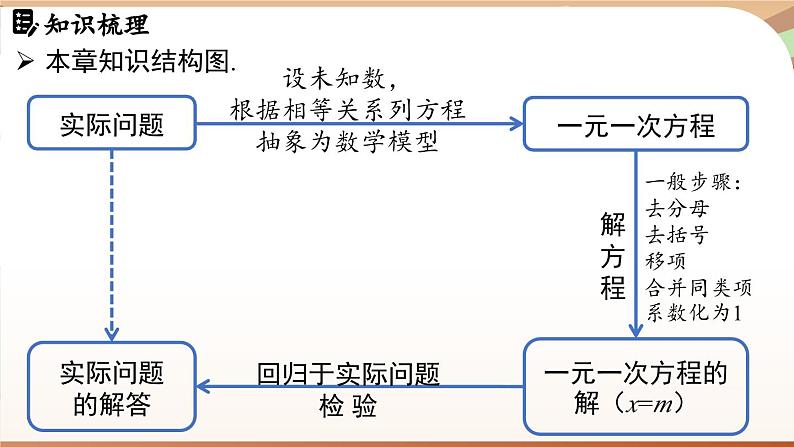
第五章 一元一次方程章末小结实际问题实际问题的解答一元一次方程一元一次方程的解(x=m)设未知数,根据相等关系列方程抽象为数学模型解方程回归于实际问题检 验本章知识结构图.一般步骤:去分母去括号移项合并同类项系数化为1一元一次方程方程:含有未知数的等式.一元一次方程:只含有一个未知数(元),且含有未知数的式子都是整式,未知数的次数都是1的方程.方程的解:使方程左、右两边的值相等的未知数的值.概念等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.性质等式的基本事实:等式两边可以交换. 相等关系可以传递.解一元一次方程的一般步骤:去分母.去括号.移项.合并同类项.系数化为1. 45%n+110=n.1.列方程表示下列语句中的相等关系:(3)一种商品每件进价为a元,售价为进价的1.1倍,现每件的售价又降低10元,现售价为每件210元;(4)在5天中,第一小组共植树60棵,第二小组共植树x(x<60)棵,平均每天第一小组比第二小组多植2棵树.1.1a-10=210. 2.已知x=-1是方程ax3+bx-3=2的解,则当x=1时,求代数式ax3+bx-3的值.解:将x=-1代入方程a(-1)3+b(-1)-3=2,即a+b=-5.当x=1时,原式=a·13+b·1-3=a+b-3=-8. (2)移项,得0.5x+1.3x=6.5+0.7合并同类项,得1.8x=7.2.系数化为1,得 x=4. 用一元一次方程解决实际问题的基本过程如下:审:审清题意,找相等关系;设:设未知数;列:列方程;解:解方程;检:检验所得结果;答:确定答案.正确分析问题中的相等关系是列方程的基础.列一元一次方程解决实际问题的类型1. 配套问题 列一元一次方程解决实际问题的类型2.工程问题工程问题中的基本数量关系:工作量=工作效率×工作时间(或人均效率×时间×人数);合作的效率=各部分单独做的效率和;总工作量=各部分工作量之和.列一元一次方程解决实际问题的类型3.销售问题 列一元一次方程解决实际问题的类型4.比赛中的积分问题在比赛积分问题中,常见的等量关系:某个队的参赛场数=该队的胜场数+该队的负场数+该队的平场数;某个队的总积分=该队的胜场积分+该队的负场积分+该队的平场积分.列一元一次方程解决实际问题的类型5.方案选择问题审题更优惠费用相同列方程用未知数表示费用设未知数选择最优方案问题的一般步骤:4.(我国古代问题)跑得快的马每天走240里,跑得慢的马每天走150里.慢马先走12天,快马几天可以追上慢马?解:设快马x天可以追上慢马.由题意,得240x=150(12+x). 解得x=20.答:快马20天可以追上慢马.5.某车间每天能制作甲种零件500只,或者制作乙种零件250只,甲、乙两种零件各一只配成一套产品,现要在30天内制作最多的成套产品,则甲、乙两种零件各应制作多少天?解:设甲种零件应制作x天,则乙种零件应制作(30-x)天.依题意,得500x=250(30-x).解得x=10.那么30-x=20.答:甲种零件应制作10天,乙种零件应制作20天. 6.某中学的学生自己动手整修操场,如果让七年级学生单独工作,需要7.5h完成;如果让八年级学生单独工作,需要5h完成.如果让七、八年级学生一起工作1h,再由八年级学生单独完成剩余部分,共需多少时间完成?7.现对某商品降价20%促销,为了使销售总金额不变,销售量要比按原价销售时增加百分之几?解:设销售量要比按原价销售时增加x%.依题意,得(1-20%)(1+x%)=1.解得x=25.答:销售量要比按原价销售时增加25%.8.学校组织知识竞赛,共设20道选择题,各题分值相同,每题必答.下表记录了5名参赛同学的得分情况.(1)同学F得76分,他答对了几道题?(2)同学G说他得了80分,你认为可能吗?为什么?解:由参赛者A知,答对一题得5分,再由参赛者B知,答错一题扣1分.(1)设同学F答对了x道题.依题意,得5x-(20-x)= 76.解得x=16.答:同学F答对了16 道题. 8.学校组织知识竞赛,共设20道选择题,各题分值相同,每题必答.下表记录了5名参赛同学的得分情况.(1)同学F得76分,他答对了几道题?(2)同学G说他得了80分,你认为可能吗?为什么?9.一家游泳馆每年6月一8月出售夏季会员证,每张会员证120元,只限本人使用,凭会员证购入场券每张15元,不凭会员证购入场券每张20元.试讨论并回答下列问题:(1)在什么情况下,使用会员证与不使用会员证付一样的钱?(2)在什么情况下,使用会员证比不使用会员证更合算?(3)在什么情况下,不使用会员证比使用会员证更合算?解:设游泳x次时,使用会员证与不使用会员证付一样的钱.根据题意,得120+15x=20x ,解得x=24.答:(1)去游泳馆24次时,使用会员证与不使用会员证付一样的钱. (2)去游泳馆的次数大于24次时,使用会员证比不使用会员证更合算.(3)去游泳馆的次数少于24次时,不使用会员证比使用会员证更合算.
第五章 一元一次方程章末小结实际问题实际问题的解答一元一次方程一元一次方程的解(x=m)设未知数,根据相等关系列方程抽象为数学模型解方程回归于实际问题检 验本章知识结构图.一般步骤:去分母去括号移项合并同类项系数化为1一元一次方程方程:含有未知数的等式.一元一次方程:只含有一个未知数(元),且含有未知数的式子都是整式,未知数的次数都是1的方程.方程的解:使方程左、右两边的值相等的未知数的值.概念等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.性质等式的基本事实:等式两边可以交换. 相等关系可以传递.解一元一次方程的一般步骤:去分母.去括号.移项.合并同类项.系数化为1. 45%n+110=n.1.列方程表示下列语句中的相等关系:(3)一种商品每件进价为a元,售价为进价的1.1倍,现每件的售价又降低10元,现售价为每件210元;(4)在5天中,第一小组共植树60棵,第二小组共植树x(x<60)棵,平均每天第一小组比第二小组多植2棵树.1.1a-10=210. 2.已知x=-1是方程ax3+bx-3=2的解,则当x=1时,求代数式ax3+bx-3的值.解:将x=-1代入方程a(-1)3+b(-1)-3=2,即a+b=-5.当x=1时,原式=a·13+b·1-3=a+b-3=-8. (2)移项,得0.5x+1.3x=6.5+0.7合并同类项,得1.8x=7.2.系数化为1,得 x=4. 用一元一次方程解决实际问题的基本过程如下:审:审清题意,找相等关系;设:设未知数;列:列方程;解:解方程;检:检验所得结果;答:确定答案.正确分析问题中的相等关系是列方程的基础.列一元一次方程解决实际问题的类型1. 配套问题 列一元一次方程解决实际问题的类型2.工程问题工程问题中的基本数量关系:工作量=工作效率×工作时间(或人均效率×时间×人数);合作的效率=各部分单独做的效率和;总工作量=各部分工作量之和.列一元一次方程解决实际问题的类型3.销售问题 列一元一次方程解决实际问题的类型4.比赛中的积分问题在比赛积分问题中,常见的等量关系:某个队的参赛场数=该队的胜场数+该队的负场数+该队的平场数;某个队的总积分=该队的胜场积分+该队的负场积分+该队的平场积分.列一元一次方程解决实际问题的类型5.方案选择问题审题更优惠费用相同列方程用未知数表示费用设未知数选择最优方案问题的一般步骤:4.(我国古代问题)跑得快的马每天走240里,跑得慢的马每天走150里.慢马先走12天,快马几天可以追上慢马?解:设快马x天可以追上慢马.由题意,得240x=150(12+x). 解得x=20.答:快马20天可以追上慢马.5.某车间每天能制作甲种零件500只,或者制作乙种零件250只,甲、乙两种零件各一只配成一套产品,现要在30天内制作最多的成套产品,则甲、乙两种零件各应制作多少天?解:设甲种零件应制作x天,则乙种零件应制作(30-x)天.依题意,得500x=250(30-x).解得x=10.那么30-x=20.答:甲种零件应制作10天,乙种零件应制作20天. 6.某中学的学生自己动手整修操场,如果让七年级学生单独工作,需要7.5h完成;如果让八年级学生单独工作,需要5h完成.如果让七、八年级学生一起工作1h,再由八年级学生单独完成剩余部分,共需多少时间完成?7.现对某商品降价20%促销,为了使销售总金额不变,销售量要比按原价销售时增加百分之几?解:设销售量要比按原价销售时增加x%.依题意,得(1-20%)(1+x%)=1.解得x=25.答:销售量要比按原价销售时增加25%.8.学校组织知识竞赛,共设20道选择题,各题分值相同,每题必答.下表记录了5名参赛同学的得分情况.(1)同学F得76分,他答对了几道题?(2)同学G说他得了80分,你认为可能吗?为什么?解:由参赛者A知,答对一题得5分,再由参赛者B知,答错一题扣1分.(1)设同学F答对了x道题.依题意,得5x-(20-x)= 76.解得x=16.答:同学F答对了16 道题. 8.学校组织知识竞赛,共设20道选择题,各题分值相同,每题必答.下表记录了5名参赛同学的得分情况.(1)同学F得76分,他答对了几道题?(2)同学G说他得了80分,你认为可能吗?为什么?9.一家游泳馆每年6月一8月出售夏季会员证,每张会员证120元,只限本人使用,凭会员证购入场券每张15元,不凭会员证购入场券每张20元.试讨论并回答下列问题:(1)在什么情况下,使用会员证与不使用会员证付一样的钱?(2)在什么情况下,使用会员证比不使用会员证更合算?(3)在什么情况下,不使用会员证比使用会员证更合算?解:设游泳x次时,使用会员证与不使用会员证付一样的钱.根据题意,得120+15x=20x ,解得x=24.答:(1)去游泳馆24次时,使用会员证与不使用会员证付一样的钱. (2)去游泳馆的次数大于24次时,使用会员证比不使用会员证更合算.(3)去游泳馆的次数少于24次时,不使用会员证比使用会员证更合算.
相关资料
更多









