2024年华东师大版七年级数学暑期提升精讲 第06讲 有理数的乘方(知识点+练习)

这是一份2024年华东师大版七年级数学暑期提升精讲 第06讲 有理数的乘方(知识点+练习)，文件包含2024年华东师大版七年级数学暑期提升精讲第06讲有理数的乘方原卷版docx、2024年华东师大版七年级数学暑期提升精讲第06讲有理数的乘方解析版docx等2份试卷配套教学资源，其中试卷共44页， 欢迎下载使用。

1.乘方
2.科学记数法
【考点一 有理数幂的概念理解】
例1．（23-24七年级上·广西北海·阶段练习）对于式子，下列说法不正确的是（ ）
A．指数是3B．底数是C．结果为D．表示3与相乘
变式1-1．（23-24七年级上·湖南长沙·期中）比较和，下列说法正确的是（ ）
A．它们底数相同，指数也相同B．它们底数相同，但指数不相同
C．D．
变式1-2．（23-24七年级上·河北唐山·期中）计算（ ）
A．B．C．D．
变式1-3．（23-24七年级上·陕西渭南·期中）已知的底数为，指数为，的底数为，幂为，则 ．
变式1-4．（23-24七年级上·河南周口·阶段练习）仔细观察下列算式：，．
(1) ；
(2) ；
(3) ．
【考点二 有理数运算的符号规律】
例2．（23-24七年级上·河南郑州·阶段练习）在，，，中负数有（ ）
A．1个B．2个C．3个D．4个
变式2-1．（21-22七年级上·江苏扬州·期末）下列代数式的值一定是正数的是（ ）
A．B．C．D．
变式2-2．（23-24七年级上·江苏常州·阶段练习）若，则的值是（ ）
A．B．1C．0D．
变式2-3．（23-24七年级上·安徽淮北·阶段练习）若字母各表示一个有理数，则下列结论错误的是（ ）
A．若，则B．若，则
C．若，则D．若，则
变式2-4．（23-24七年级上·浙江绍兴·阶段练习） ．
变式2-5．（23-24七年级上·河南漯河·阶段练习）当整数为 时，；若是正整数，则 ．
【考点三 有理数乘方的运算】
例3．（23-24七年级上·江苏连云港·阶段练习）已知，，且，求的值．
变式3-1．（23-24七年级上·四川泸州·阶段练习）已知，求的值．
变式3-2．（23-24七年级上·江苏无锡·期中）现有一组数：、、、、、，请回答下列问题：
(1)这组数中所有负数的和为______；
(2)若一组数中的服大值与最小值的差称为极差，则这组数的极差为______；
(3)画出数轴，并在数轴上表示这一组数，再用“1? 1a>1bD．
7．（23-24六年级下·全国·假期作业）若，则有理数a在数轴上的对应点一定在（ ）
A．原点左侧B．原点或原点左侧C．原点右侧D．原点或原点右侧
8．（23-24六年级下·全国·假期作业）用科学记数法表示为（ ）
A．B．C．D．
9．（2024·河北廊坊·二模）已知：，则（ ）
A．B．C．D．
10．（2024·河南郑州·三模）“北斗系统”是我国自主建设运行的全球卫星导航系统，国内多个导航地图采用北斗优先定位．目前，北斗定位服务日均使用量已超过万亿次，万亿用科学记数法表示为( )
A．B．C．D．
11．（2024·河北邯郸·三模）杭州亚运会开幕式上，约105800000名“数字火炬人”和现场火炬手共同点燃了主火炬塔，实现了首个“数实融合”的点火仪式，将数据105800000用科学记数法表示为的形式，则a的值为（ ）
A．0.1058B．1.058C．10.58D．1058
二、填空题
12．（24-25七年级上·全国·假期作业）计算： ， ， ．
13．（23-24七年级下·四川成都·期中）已知a，b满足，那么 ．
14．（23-24六年级下·上海普陀·期中）9个2相乘的结果用幂的形式表示为 ．
15．（23-24九年级下·山东青岛·期中）利用如图1的二维码可以进行身份识别，某校建立了一个身份识别系统，图2是某个学生的识别图案，黑色小正方形表示1，白色小正方形表示0，将第一行数字从左到右依次记为，，，，那么可以转换为该生所在班级序号，其序号为，如图2第一行数字从左到右依次为0，1，0，1，序号为，表示该生为5班学生．表示6班学生的识别图案是 ．
16．（23-24七年级下·江苏盐城·期中）如果，则，例如，则．根据规定，若，则 ．
17．（23-24七年级上·河南郑州·期中）2023年国庆期间，郑州新彩虹桥顺利通车．通车当天搜索“郑州新彩虹桥”，找到相关结果用科学记数法表示为个，则原数是 个．
三、解答题
18．（23-24六年级下·全国·假期作业）下列用科学记数法表示的数，原数分别是什么？
(1)；
(2)；
(3)．
19．（23-24七年级下·广东佛山·阶段练习）计算：
20．（24-25七年级上·全国·假期作业）把下列各式写成乘方的形式，并指出底数和指数各是什么．
(1)；
(2)
21．（23-24六年级下·全国·假期作业）阅读下面的材料，然后按照材料中提供的方法计算．
计算：．
解：设，
则，
所以
，
即．
按照上面的方法，计算：．
22．（23-24七年级下·河北石家庄·期中）观察下列算式：
①
②
③
…
(1)请你按以上规律写出第4个算式；
(2)把这个规律用含字母n的式子表示出来，并用学过的整式乘法的有关知识，说明其成立的理由．
23．（23-24六年级下·山东烟台·期中）阅读材料，回答问题．
材料一：因为，所以．
材料二：求的值．
解：设①，
①两边同时乘以3得，则②
用得，
所以，
即，
所以．
这种方法我们称为“错位相减法”．
(1)填空：_________，_________；
(2)“棋盘摆米”是一个著名的数学故事：阿基米德与国王下棋，国王输了，国王问阿基米德要什么奖赏．阿基米德对国王说：“我只要在棋盘上第一格放一粒米，第二格放二粒，第三格放四粒，第四格放八粒…按这个方法放满整个棋盘就行”国王以为要不了多少粮食，就随口答应了．
①国际象棋共有64个格子，则在第64格中应放_________粒米（用幂表示）；
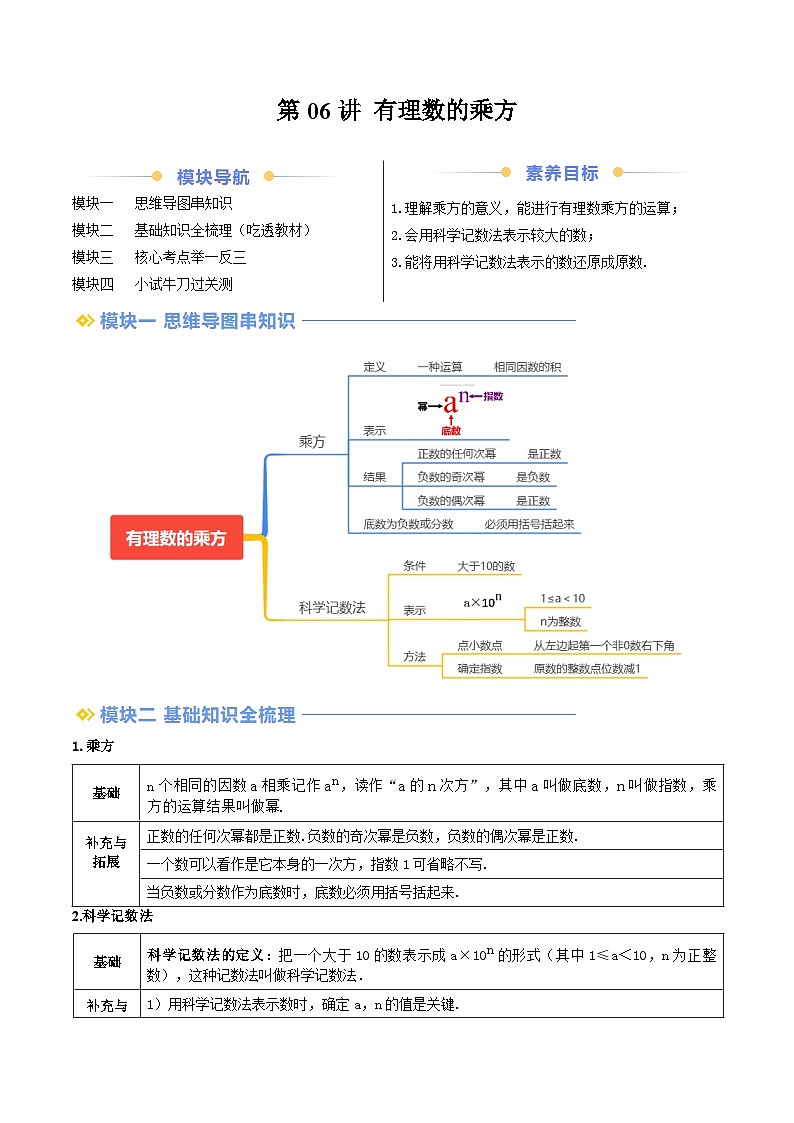
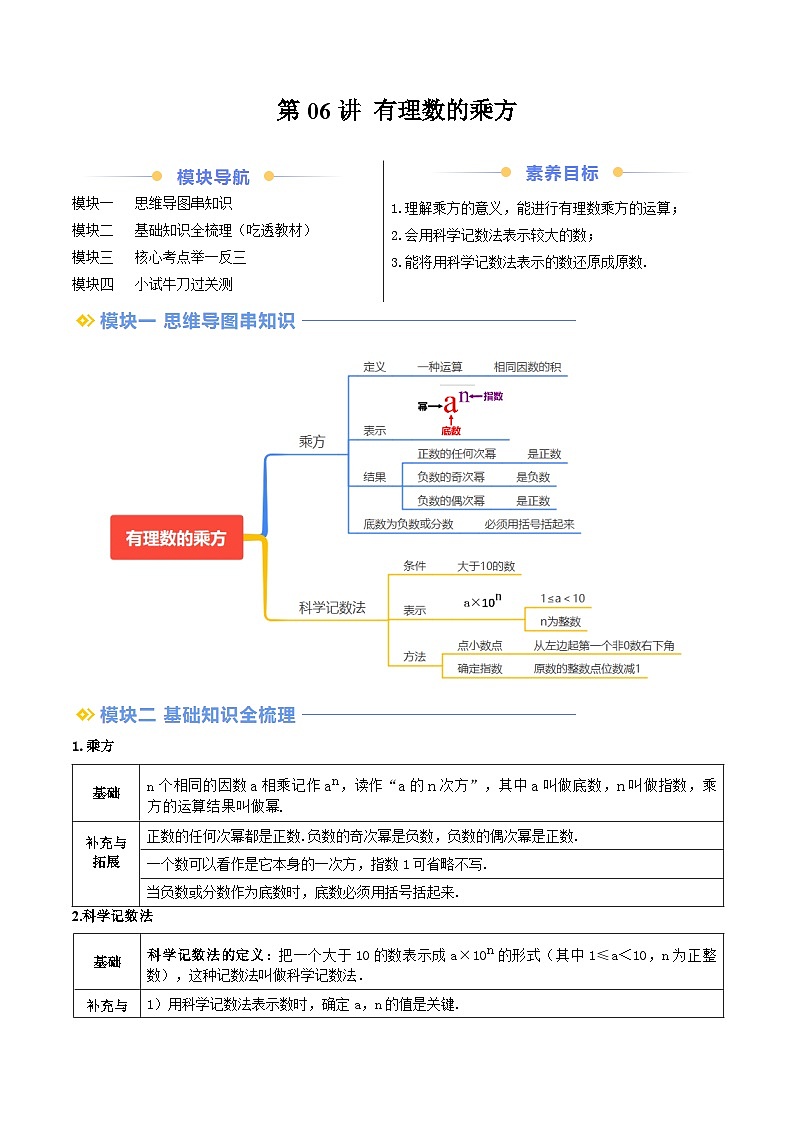
②设国王输给阿基米德的总米粒数为S，求S．模块一 思维导图串知识
模块二 基础知识全梳理（吃透教材）
模块三 核心考点举一反三
模块四 小试牛刀过关测
1.理解乘方的意义，能进行有理数乘方的运算；
2.会用科学记数法表示较大的数；
3.能将用科学记数法表示的数还原成原数.
基础
n个相同的因数a相乘记作an，读作“a的n次方”，其中a叫做底数，n叫做指数，乘方的运算结果叫做幂.
补充与拓展
正数的任何次幂都是正数.负数的奇次幂是负数，负数的偶次幂是正数.
一个数可以看作是它本身的一次方，指数1可省略不写.
当负数或分数作为底数时，底数必须用括号括起来.
基础
科学记数法的定义：把一个大于10的数表示成a×10n的形式（其中1≤a＜10，n为正整数），这种记数法叫做科学记数法．
补充与拓展
1）用科学记数法表示数时，确定a，n的值是关键.
①a是一个整数数位只有一位的数，即1≤a＜10;
②确定n的方法：当原数绝对值大于10时，则n等于原数的整数位数减1；
2）还原用科学记数法表示的数时，n＞0时，小数点就向右移动n位得到原数；
小技巧：1万=104，1亿=1万*1万=108
个位数
0
1
2
3
4
5
6
7
8
9
个位数
0
1
4
9
6
5
6
9
4
1
个位数
0
1
8
7
4
5
6
3
2
9
个位数
0
1
6
1
6
5
6
1
6
1
······