2024年华东师大版七年级数学暑期提升精讲 第10讲 有理数中规律和新定义综合应用的八大题型(知识点+练习)

这是一份2024年华东师大版七年级数学暑期提升精讲 第10讲 有理数中规律和新定义综合应用的八大题型(知识点+练习)，文件包含2024年华东师大版七年级数学暑期提升精讲第10讲有理数中规律和新定义综合应用的八大题型原卷版docx、2024年华东师大版七年级数学暑期提升精讲第10讲有理数中规律和新定义综合应用的八大题型解析版docx等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。


【题型一 数列型规律探究 - 等差数列】
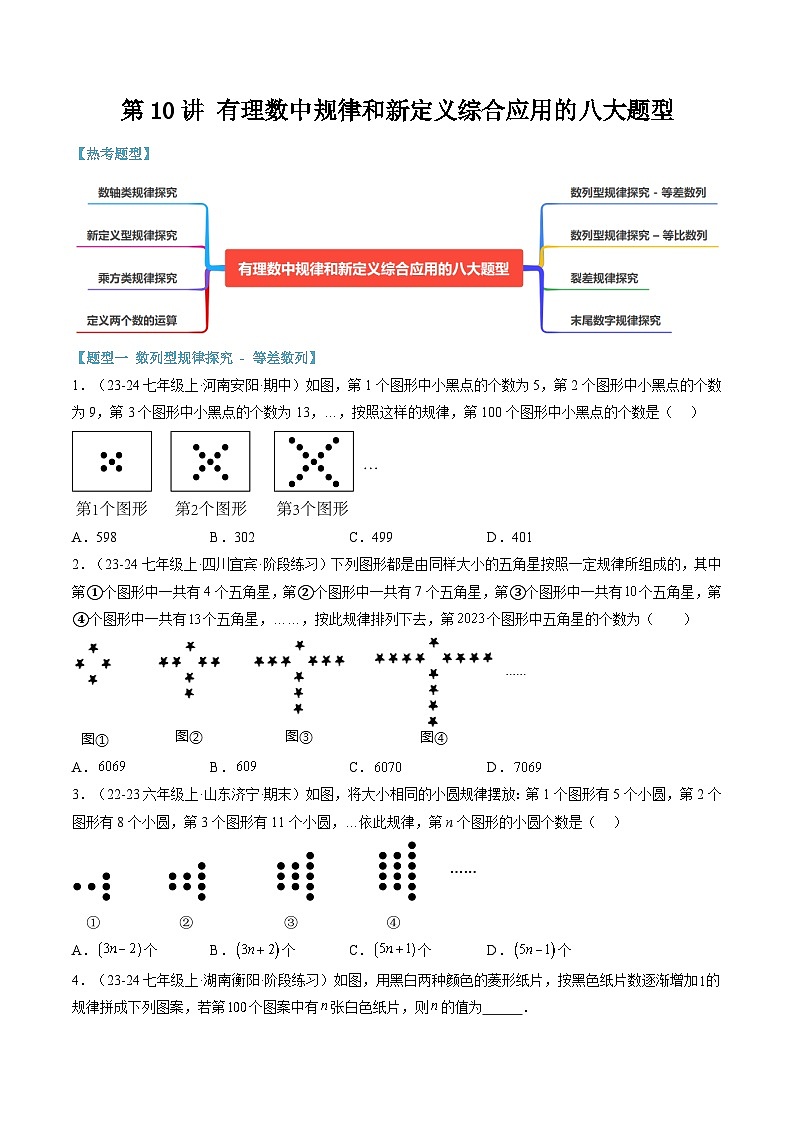
1．（23-24七年级上·河南安阳·期中）如图，第1个图形中小黑点的个数为5，第2个图形中小黑点的个数为9，第3个图形中小黑点的个数为13，…，按照这样的规律，第100个图形中小黑点的个数是（ ）

A．598B．302C．499D．401
【答案】D
【分析】本题考查图形变化的规律，有理数的混合运算，能发现每个图形中小黑点的个数除去中间一个后，其余的小黑点个数是4的倍数进行解题即可．
【详解】解：由题知：
第1个图形中小黑点的个数为：，
第2个图形中小黑点的个数为：，
第3个图形中小黑点的个数为：，
则第100个图形中小黑点的个数为：，
故选：D．
2．（23-24七年级上·四川宜宾·阶段练习）下列图形都是由同样大小的五角星按照一定规律所组成的，其中第①个图形中一共有4个五角星，第②个图形中一共有7个五角星，第③个图形中一共有个五角星，第④个图形中一共有个五角星，……，按此规律排列下去，第个图形中五角星的个数为（ ）
A．B．C．D．
【答案】C
【分析】根据图形的变化即可写出规律式，进而求解．
【详解】解：观察图形的变化可知：
第①个图形中一共有4个五角星，即；
第②个图形中一共有7个五角星，即；
第③个图形中一共有个五角星，即；
第④个图形中一共有个五角星，即；
……，按此规律排列下去，
第n个图形中一共有五角星个数为，
第个图形中五角星的个数为，
故选：C．
【点睛】本题考查了图形的变化类，以及有理数的加法和乘法运算，解决本题的关键是观察图形的变化寻找规律．
3．（22-23六年级上·山东济宁·期末）如图，将大小相同的小圆规律摆放：第1个图形有5个小圆，第2个图形有8个小圆，第3个图形有11个小圆，…依此规律，第n个图形的小圆个数是（ ）
A．个B．个C．个D．个
【答案】B
【分析】观察图形的变化先计算出前几个图形的小圆的个数，进而可得第n个图形的小圆个数．
【详解】解：观察图形的变化可知：第1个图形有5个小圆，即，
第2个图形有8个小圆，即，
第3个图形有11个小圆，即，
依此规律，第n个图形的小圆个数是： ，
故选：B．
【点睛】本题考查了图形的变化规律，解题的关键是先计算出前几个图形的小圆的个数，找到规律．
4．（23-24七年级上·湖南衡阳·阶段练习）如图，用黑白两种颜色的菱形纸片，按黑色纸片数逐渐增加的规律拼成下列图案，若第个图案中有张白色纸片，则的值为 ．

【答案】
【分析】根据图形的排序和数量关系，列式计算即可求解．
【详解】解：由图可得，
第个图案中白色纸片的个数为：，
第个图案中白色纸片的个数为：，
第个图案中白色纸片的个数为：，
……，
第个图案中白色纸片的个数为：，
故答案为：．
【点睛】本题主要考查图形规律，理解图示中排序和图形数量关系，掌握有理数的混合运算是解题的关键．
5．（22-23八年级下·云南红河·期末）下列图形是由一些大小相同的十字星按一定规律组合而成的，按此规律排列的第个图中共有 个十字星．

【答案】
【分析】先根据题中的图形进行研究，分析出图形规律即可作答．
【详解】解：第一个图的十字星是2个；
第二个图的十字星是（个）；
第三个图的十字星是（个）；
第四个图的十字星是（个）；
……
依次类推，则第n个图的十字星是（个）；
所以第个图中，即，
故第个图的十字星是（个），
故答案为：．
【点睛】本题考查了图形规律，涉及有理数的乘法和加减法运算，解题的关键是研究出图形的规律．
6．（23-24七年级上·广西南宁·期中）如图是一组有规律的图案，它们是由边长相同的正方形和等边三角形镶嵌而成，按照这样的规律继续摆下去，第 个图案有个三角形．
【答案】
【分析】此题考查图形的变化规律，由题意可知：第（1）个图案有个三角形，第（2）个图案有个三角形，第（3）个图案有个三角形，…依此规律，第n个图案有个三角形，进而得出方程解答即可．找出图形之间的运算规律，利用规律解决问题．
【详解】解：∵第（1）个图案有个三角形，
第（2）个图案有个三角形，
第（3）个图案有个三角形，
第（4）个图案有个三角形，
…，
∴第n个图案有个三角形．
根据题意可得：，
解得：，
∴第个图案有个三角形，
故答案为：．
7．（23-24七年级上·湖北黄石·阶段练习）根据下面的图形中圆个数的变化规律，第个图形中有( )个圆，第个图形中有( )个圆．

【答案】
【分析】根据图形的排序、数量找出规律，即可求解．
【详解】解：第个图形的数量为；
第个图形的数量为；
第个图形的数量为；
……
∴第个图形的数量为；
∴第个图形的数量为；
故答案为：，．
【点睛】本题主要考查图形规律，有理数的混合运算，理解题目中图形的排序，数量的关系，掌握有理数的混合运算法则是解题的关键．
【题型二 数列型规律探究 – 等比数列】
8．（23-24七年级上·黑龙江绥化·阶段练习）观察一组按规律排列的数：1，2，4，8，，…，则第个数是（ ）．
A．B．C．D．以上答案都不对
【答案】C
【分析】根据1，2，4，8，，…，得出第个数为，把代入即可作答．
【详解】解：观察所给的数据，
得第个数为，
当时，，
故选：C．
【点睛】本题考查了数字规律，解题的关键找出第个数为，难度较小．
9．（22-23七年级上·重庆江津·阶段练习）下列一组按规律排列的数：1，2，4，8，16，…第2021个数是（ ）
A．B．
C．D．以上答案都不对
【答案】C
【分析】通过计算得到，是第1个数；，是第2个数；，是第3个数；，是第4个数；，是第5个数，则数的序号比指数大1，于是得到第2021个数是．
【详解】解：∵一组按规律排列的数：1，2，4，8，16，…，
∴这些数变为：，…，
∴第2021个数是．
故选：C．
【点睛】本题考查了规律型—数字的变化类：通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．
【题型三 裂差规律探究】
10．（23-24七年级上·江苏南京·阶段练习）如图，把一个面积为1的正方形等分成两个面积为的长方形，接着把面积为的长方形等分成两个面积为的正方形，再把面积为的正方形等分成两个面积为的长方形……如此进行下去，试利用图形揭示的规律计算： ．

【答案】
【分析】结合图象发现计算方法：，，即计算面积等于总面积减去剩余面积．
【详解】解：根据图示可知，
，
，
，
∴．
故答案为：．
【点睛】本题主要考查了平面图形的有规律变化，要求学生通过观察图形，分析、归纳并发现其中的规律，并应用规律解决问题，是解题的关键．
11．（22-23七年级上·广东韶关·期末）已知：，，，……
（1）请按以上规律接着写出： ；
（2）计算： ．
【答案】
【分析】（1）依据题干规律直接列式即可；
（2）依据题干给出的等式，将原式变型，再计算即可．
【详解】（1）依据题干规律直接列式为：，
故答案为：；
（2）
，
故答案为：．
【点睛】本题主要考查了有理数的混合运算，准确分析计算是解题的关键．
12．（22-23八年级上·山东潍坊·期末）观察下列各式：，，，……根据你发现的规律，计算： ．
【答案】2022
【分析】根据题目中式子的特点，通过裂项抵消的方法可以解答本题．
【详解】解：由题意，归纳类推得：，
∴
．
故答案为：2022．
【点睛】本题考查数字的变化类、有理数的混合运算，解答本题的关键是明确题意，发现题目中式子的特点，求出所求式子的值．
13．（22-23七年级下·湖南永州·开学考试）如图所示，将形状、大小完全相同的“•”和线段按照一定规律摆成下列图形，第1幅图形中“•”的个数为，第2幅图形中“•”的个数为，第3幅图形中“•”的个数为，以此类推，则的值为 .

【答案】
【分析】首先根据图形中“•”的个数得出数字变化规律，进而求出即可．
【详解】解：，
，
，
，
；
故答案为：．
【点睛】此题考查图形的变化规律，找出图形之间的联系，找出规律解决问题．
14．（23-24七年级·江苏·假期作业）观察下列等式：；；……，，请根据上面计算规律计算= ．
【答案】
【分析】根据所给的等式的形式，对所求的式子进行整理，从而可求解．
【详解】解：
＝
＝
＝
＝；
故答案为：．
【点睛】本题主要考查数字的变化规律，有理数的混合运算，解答的关键是理解清楚所给的式子的规律并灵活运用．
15．（23-24七年级上·广西南宁·阶段练习）观察下列各式：，，，，……，按照上面的规律，计算： ．
【答案】
【分析】根据式子的规律得出，进而化简式子，根据有理数的加减进行计算，最后求绝对值即可求解．
【详解】解：∵，，，，……，
∴，
∴
，
故答案为：．
【点睛】本题考查了有理数的加减混合运算，找到规律是解题的关键．
16．（21-22七年级上·浙江丽水·期中）观察下列等式：
第1个等式：；
第2个等式：；
第3个等式：；
第4个等式：．
解答下列问题：
（1）按以上规律写出第5个等式： ；
（2） ．
【答案】
【分析】（1）根据题目所给规律，直接可写出第5个等式．
（2）利用题目的规律，进行等式变形，提取，括号里面的前一项和后一项数可以抵消掉，最后求得结果．
【详解】（1）解：由上述规律可知：
故答案为：．
（2）解：原式=



．
故答案为：．
【点睛】本题主要是考查了数字的规律以及利用规律进行计算，通过题目所给条件，找到对应的规律，并应用规律进行求解，是解决本题的关键．
17．（22-23七年级上·四川达州·期末）如图所示，将形状大小完全相同的“”按照一定规律摆成下列图形，第1幅图中“”的个数为，第2幅图中“”的个数为，第3幅图中“”的个数为…，以此类推，的值为 ．
【答案】
【分析】先根据已知图形得出，代入再利用裂项化简可得答案．
【详解】解：由图形知，，，
，
，
，
故答案为：．
【点睛】本题主要考查图形的变化规律，解题的关键是根据已知图形得出及．
18．（21-22七年级上·云南德宏·阶段练习）观察下面的一列数，按某种规律在横线上填上适当的数：、、、，…，第6个数是 ，第100个数是 ．
【答案】
【分析】观察数的规律可知，每一项都是分数，且分子为1，分母为该数的序号与比该数的序号多1的数的积，即第n个数为；利用计算即可．
【详解】解：第1个数：；
第2个数：；
第3个数：；
…
∴第6个数是
∴第100个数：；
故答案为：，．
【点睛】本题考查了数字的变化规律及有理数的加法运算，解题的关键是学会从特殊到一般的探究方法，属于中考常考题型．
【题型四 末尾数字规律探究】
19．（22-23七年级上·河南洛阳·期中）计算：，，，…归纳计算结果中的个位数字的规律，猜测个位数字是 ．
【答案】0
【分析】通过观察所给的运算结果，发现每4次运算结果的尾数循环一次出现，则可知个位数字与3的个位数字相同，由此求解即可．
【详解】解：∵，，，，，…，
∴每4次运算结果的尾数循环一次出现，
∵……2，
∴个位数字与的个位数字相同，是9，
∴个位数字是0，
故答案为：0．
【点睛】本题考查的是有理数的乘方，通过观察所给的运算结果，探索出结果的尾数的循环规律是解题的关键．
20．（20-21七年级上·海南省直辖县级单位·期中）观察下列算式发现规律：，，，，，，……，则的个位数字是 ．
【答案】1
【分析】根据7的指数从1到5，末位数字从7，9，3，1，7进行循环，再用2020除以4得出余数，再写出72020个位数字．
【详解】解：∵71=7，72=49，73=343，74=2401，75=16807，76=117649，上述的几个式子，易知1次方为末位数字是7，2次方末位数字是为9，3次方末位数字是为3，4次方末位数字是为1，5次方末位数字是为7，
∴个位数字的变化是以7，9，3，1为周期，即周期为4，
∵2020÷4=505，
∴72020的个位数字为1，
故答案为：1．
【点睛】此题主要考查了尾数特征，观察出结果个位数字的特点是解本题的关键．
21．（20-21七年级上·辽宁铁岭·期末）观察下列等式：31＝3，32＝9，33＝27，34＝81，35＝243，36＝729，37＝2187，38＝6561，39＝19683，…，它们的个位数字有什么规律，用你发现的规律直接写出31+32+33+34+…+3366的个位数字是 ．
【答案】2
【分析】根据题目中的数字和数字，可以写出前几个式子的值，从而可以发现这些式子结果的个位数字的变化特点，从而可以得到所求式子的个位数字．
【详解】解：由题意可得，
31＝3，
31+32＝12，
31+32+33＝39，
31+32+33+34＝120，
31+32+33+34+35＝363，
31+32+33+34+35+36＝1092，
…，
由上可得，这列式子的结果的个位数字依次以3，2，9，0循环出现，
∵366÷4＝91…2，
∴31+32+33+34+…+3366的个位数字是2，
故答案为：2．
【点睛】本题考查数字的变化类、尾数特征，解答本题的关键是明确题意，发现式子的结果个位数字的变化特点，求出所求式子的结果的个位数字．
22．（20-21七年级上·甘肃白银·期中）观察下列算式：，，，，，，，…通过观察，用你所发现的规律写出22020+1的末位数字是 ．
【答案】7
【分析】先找出规律，再求出2020÷4的值，根据规律得出即可．
【详解】解：∵21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256，…
∴尾数每4个循环一次，
2020÷4=505，
∴22020的末位数字是6，22020+1的末位数字是7，
故答案为：7．
【点睛】本题考查了有理数的乘方的应用，关键是找出已知算式所反映的规律．
【题型五 数轴类规律探究】
23．（23-24七年级上·广东云浮·期末）如图所示，数轴上O，A两点的距离为12，一动点P从点A出发，按以下规律跳动：第1次跳动到的中点处，第2次从点跳动到的中点处，第3次从点跳动到的中点处．按照这样的规律继续跳动到点，，…（，n是整数）处，问经过这样2023次跳动后的点与的中点的距离是（ ）．
A．B．
C．D．
【答案】B
【分析】本题主要考查了图形类的规律，数轴上两点的距离，，准确分析计算是解题的关键．根据题意得出表示的数为，则点表示的数为，在得出的中点表示的数为9，即可解答．
【详解】解：根据题意可得：
∵数轴上O，A两点的距离为12，
∴点A表示的数为12，
表示的数为，
表示的数为，
表示的数为，
表示的数为，
……
表示的数为，
∴经过这样2023次跳动后的点表示的数为，
∵点A表示的数为12，表示的数为6，
∴的中点表示的数为，
∴经过这样2023次跳动后的点与的中点的距离为，
故选：B．
24．（23-24七年级上·辽宁丹东·期中）一个动点P从数轴上原点O出发开始移动，第1次向右移动1个单位长度到达点，第2次向右移动2个单位长度到达点，第3次向左移动3个单位长度到达点，第4次向左移动4个单位长度到达点，第5次向右移动5个单位长度到达点，…，点P按此规律移动，则移动第次后到达点在数轴上表示的数为（ ）
A．B．C．D．
【答案】B
【分析】本题考查数字的变化规律，分别求出部分点表示的数，发现规律为每移动四次相当于向左移动4个单位长度，再由，可得，即为在数轴上表示的数．
【详解】解：∵表示的数为，表示的数为，表示的数为0，表示的数为，表示的数为，，
∴每移动四次相当于向左移动4个单位长度，
∵，
∴，
∴在数轴上表示的数为，
故选：B．
25．（22-23七年级上·山西晋中·期中）点，，，……，（为正整数）都在数轴上，点在原点点的左边，且；点在点的右边，且；点在点的左边，且；点在点点的右边，且；……，依照上述规律，点，所表示的数分别为（ ）
A．，B．，C．，D．，
【答案】B
【分析】依据表示的数为，表示的数为，表示的数为，表示的数为，……，即可得出规律：当n为奇数时，表示的数为；当为偶数时，表示的数为，进而得到答案．
【详解】解：由题意可得：表示的数为，表示的数为，表示的数为，表示的数为，……，
当n为奇数时，表示的数为，
当为偶数时，表示的数为，
∴点表示的数分别为，所表示的数分别为．
故选：B．
【点睛】本题考查数轴，规律型：数字的变化类，认真观察、仔细思考，善用联想是解决这类问题的方法，通常将数字与序号建立数量关系或者与前后数字进行简单运算，从而得出公式．
26．（23-24七年级上·湖北荆门·期末）如图，在数轴上，点A表示1，现将点A沿x轴做如下移动，第一次点A向左移动3个单位长度到达点，第二次将点向右移动6个单位长度到达点，第三次将点向左移动9个单位长度到达点，按照这种移动规律移动下去，第n次移动到点，若点与原点的距离是3035，则 ．
【答案】2023
【分析】本题考查了数轴上点的数字的变化规律，根据数轴上点的运动规律归纳出当n为奇数时，，，当n为偶数时，，，即可解答．
【详解】解：根据题意可得：，
，
，
，
……
当n为奇数时，，，
当n为偶数时，，
当，解得：，
当，解得：（舍去），
故答案为：2023．
27．（23-24七年级上·福建泉州·期中）如图，在数轴上，点表示，现将点沿数轴做如下移动：第一次点向左移动个单位长度到达点，第二次将点向右移动个单位长度到达点，第三次将点向左移动个单位长度到达点，按照这种移动规律移动下去，第次移动到点，当时，对应的数为 ，如果点与原点的距离大于，那么的值至少是 ．
【答案】
【分析】本题考查了数字的变化规律探究，根据点的移动规律，通过计算，由所表示的数找到规律，把代入即可解答；根据点与原点的距离大于，分是奇数和偶数两种情况列出对应的不等式，解之即可求解；通过计算探究出移动后的点表示的数字的变化规律是解题的关键．
【详解】解：由题可得：表示的数是，表示的数是，表示的数是，表示的数是，，
第次移动表示的数为，当是奇数时，表示的数是；当是偶数时，表示的数是；
∴时，，
故答案为：；
当时，解得，此时的最小值 为；
当时，解得，此时的最小值 为；
∴的最小值 为，
故答案为：．
【题型六 新定义型规律探究】
28．（23-24七年级上·湖北襄阳·期末）探究规律，完成相关题目，王老师说：我定义了一种新的运算，叫“※”运算．王老师写了一些按照“※”运算法则进行运算的式子：；；；；；．请你按照王老师定义的运算法则计算的结果为（ ）
A．B．C．D．
【答案】D
【分析】此题考查了实数的新定义问题，解题的关键是得出新定义的运算法则．根据题意可以得“※”的运算法则为：两数进行“※”运算时，同号得负，异号得正，并把绝对值相加，和任何数进行运算都等于这个数的相反数，任何数与进行运算都等于这个数的相反数，由此求解即可．
【详解】解：
故选：D．
29．（20-21九年级上·湖南常德·期末）符号“”表示一种运算，它对一些数的运算结果如下：
····
····
利用以上规律计算：等于（ ）
A．B．C．D．
【答案】B
【分析】根据题意，分析可得，，据此计算即可．
【详解】解：∵，
，
分析可得：，，
∴==2014，
故选B．
【点睛】此题主要考查了有理数的混合运算，数字变化规律，通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题．
30．（23-24七年级上·安徽池州·期中）规定“g”表示一种运算，它对一些数的运算结果如下：
（1），，，，……
（2），，，，……
利用以上规律计算：① ；
②根据（1）的规律求 （n为正整数）．
【答案】
【分析】本题考查了数字类规律探索，根据已知运算结果，得出相应的规律：、，据此计算即可得到答案．
【详解】解：由（1）可知，当是奇数时，符号为正，当是偶数时，符号为负，且数值为，
即；
由（2）可知，数值为的倒数减1，
即，
①，
故答案为：；
②根据（1）的规律求（n为正整数），
故答案为：．
31．（23-24七年级上·浙江杭州·期中）探究规律，完成相关题目：
小明说：“我定义了一种新的运算，叫※（加乘）运算．”
然后他写出了一些按照※（加乘）运算的运算法则进行运算的算式：
；；
；；
；；；．
小亮看了这些算式后说：“我知道你定义的※（加乘）运算的运算法则了．”
聪明的你也明白了吗？
(1)观察以上式子，类比计算：
① ， ；
(2)计算：；（括号的作用与它在有理数运算中的作用一致，写出必要的运算步骤）
(3)若．计算：的值．
【答案】(1)①；②；
(2)
(3)
【分析】本题考查了有理数的新定义运算，正确理解新定义掌握有理数的运算法则是解题的关键．
（1）根据题意得出：同号得正，异号得负，并把绝对值相加的运算法则依次计算即可．
（2）根据零与任意数※（加乘）或任何数同零※（加乘），都得这个数的绝对值，结合前面的运算计算即可；
（3）根据题意得出，确定，然后代入式子进行计算即可．
【详解】（1）解：①
=，
故答案为：．
②
=，
故答案为：．
（2）解：
=
．
（3）∵，
∴，
∴，
∴
．
32．（23-24七年级上·河南郑州·阶段练习）探究规律，完成相关题目．
定义“（环加）”运算：；；；；；．
(1)归纳运算的法则：两数进行运算时，____________，特别地，0和任何数进行运算，或任何数和0进行运算，____________．
(2)计算：______．
(3)是否存在有理数a，b，使得，若存在，求出a，b的值，若不存在，说明理由．
【答案】(1)同号得正，异号得负，并把它们的绝对值相加；都得这个数的绝对值；
(2)
(3)存在，．
【分析】（1）根据定义得出法则即可；
（2）根据法则计算即可；
（3）根据法则和非负数的性质，即可证得．
【详解】（1）解：归纳⊕运算的法则：两数进行运算时，同号得正，异号得负，并把它们的绝对值相加．特别地，0和任何数进行运算，或任何数和进行运算，都得这个数的绝对值．
故答案为：同号得正，异号得负，并把它们的绝对值相加；都得这个数的绝对值；
（2）
（3）当时，，
根据法则：，根据非负数的性质，只有时，．
【点睛】本题考查了新定义运算，理解题意是解题的关键．
33．（23-24七年级上·江苏南京·阶段练习）课堂上，老师说：“我定义了一种新的运算，叫☆运算．”老师根据规律，写出了几组按照☆运算法则进行运算的式子：
第一组：；；
第二组：；；
第三组：；；；．
小明说：我知道老师定义的☆运算法则了，聪明的你看出来了吗？请你帮忙归纳☆运算法则：
(1)归纳☆运算法则，填写下列空白部分：
①同号两个数进行☆运算时，结果的符号为负，数值部分取绝对值相加；
②异号两个数进行☆运算时，____________；
③特别地，0和任何数进行☆运算，或是任何数和0进行☆运算都等于______；
(2)填空：______；______；
(3)若，求的值．
【答案】(1)结果的符号为正，数值部分取绝对值相加；该数的绝对值
(2)；
(3)或1
【分析】（1）从题中分别观察同号运算，异号运算，以及与0进行运算时的结果，进行总结即可；
（2）结合新定义的运算法则，求解即可；
（3）分为负数、为正数和为0三种情况，分别求解即可．
【详解】（1）解：归纳☆运算法则，填写下列空白部分：
①同号两个数进行☆运算时，结果的符号为负，数值部分取绝对值相加；
②异号两个数进行☆运算时，结果的符号为正，数值部分取绝对值相加；
③特别地，0和任何数进行☆运算，或是任何数和0进行☆运算都等于该数的绝对值．
故答案为：结果的符号为正，数值部分取绝对值相加；该数的绝对值；
（2）；
．
故答案为：；；
（3）若为负数，即，
则有，
解得；
若为正数，即，
则有，
解得；
若为0，
则有，
解得，不符合题意，舍去．
综上所述，的值为或1．
【点睛】本题主要考查了新定义运算、有理数运算、化简绝对值以及解一元一次方程等知识，理解新定义的运算是解题关键．
【题型七 乘方类规律探究】
34．（22-23七年级上·广东深圳·期中）任意大于1的正整数的三次幂均可“分裂”成个连续奇数的和，如：，按此规律，若分裂后，其中有一个奇数是2023，则的值是（ ）
A．46B．45C．44D．43
【答案】B
【分析】观察可知，分裂成的奇数的个数与底数相同，然后求出到的所有奇数的个数的表达式，再求出奇数2023的是从3开始的第1011个数，然后确定出1011所在的范围即可得解．
【详解】解：∵底数是2的分裂成2个奇数和，底数为3的分裂成3个奇数和，底数为4的分裂成4个奇数和，
∴分裂成m个奇数，
所以，从到的奇数的个数为：，
，
，
∴奇数2023是从3开始的第1011个奇数，
，，
∴第1011个奇数是底数为45的数的立方分裂的奇数的其中一个，
即．
故选：B．
【点睛】本题考查了数字变化规律，有理数的混合运算，观察出分裂的奇数的个数与底数相同是解题的关键，还要熟练掌握求和公式．
35．（23-24七年级上·河北唐山·期中）通过计算器计算发现：，，……，按照以上的规律计算的结果是（ ）
A．123454321B．1234564321
C．1234567654321D．123456787654321
【答案】C
【分析】根据已知条件可以得到这样的规律：对于由1组成的数字，当平方后最中间的数字是几，这个数字就是由几个1组成．
【详解】解：根据已知条件可以得到这样的规律： 11的平方是121，中间的数字是2，111的平方是12321，中间的数字是3，…… 由此可以推断出：对于由1组成的数字，当平方后最中间的数字是几，这个数字就是由几个1组成；所以的结果是1234567654321，
故选C．
【点睛】本题主要考查了观察式子找规律，找到对于由1组成的数字，当平方后最中间的数字是几，这个数字就是由几个1组成的规律是解题的关键．
36．（20-21七年级上·安徽亳州·期中）“数形结合”是一种重要的数学思维，观察下面的图形和算式：
解答下列问题：请用上面得到的规律计算：（ ）
A．2010B．2015C．2020D．2025
【答案】D
【分析】观察图形和算式的变化发现规律，进而根据得到的规律计算即可．
【详解】解：观察以下算式：
发现规律：，
∵2n-1=89
解得n=45，
∴，
故选D．
【点睛】本题考查了规律型——图形的变化类，有理数的乘方．解题的关键是根据图形和算式的变化寻找规律．
37．（23-24七年级上·江苏常州·期中）我们根据乘方运算，得出了一种新的运算，如下表是两种运算对应关系的一组实例：
根据上表规律，某同学写出了三个式子： ①，②，③．其中正确的是 ．
【答案】/③①
【分析】本题考查了有理数的混合运算、新定义，根据题中的新定义法则判断即可，解题的关键是理解题中的新定义，熟练掌握有理数的混合运算法则．
【详解】解：，
，故①计算正确，符合题意；
，
，故②计算错误，不符合题意；
，
，故③计算正确，符合题意；
综上所述，正确的有，
故答案为：．
38．（20-21七年级上·北京西城·期末）观察下列等式，探究其中的规律并回答问题：
，
，
，
，
……
（1）第4个等式中正整数的值是 ；
（2）第5个等式是： ；
（3）第个等式是： （其中是正整数）．
【答案】 9
【分析】（1）计算有理数加法求值即可；
（2）根据已知等式的规律直接得到答案即可；
（3）根据已知等式发现规律：此列数是从1加到，等于连续奇数的平方，此奇数表示为，由此列式即可．
【详解】解：（1），
∴或（舍去），
故答案为：9；
（2）第个等式是，
故答案为：；
（3）第n个等式是：，
故答案为：．
【点睛】此题考查有理数运算规律探究，有理数的加法计算法则，连续奇数或偶数的表示方法，根据已知等式发现规律并运用规律解决问题是解题的关键．
【题型八 定义两个数的运算】
39．（23-24七年级上·广西南宁·阶段练习）现定义新运算“”，对任意有理数，规定，例，则计算（ ）
A．B．C．7D．13
【答案】B
【分析】本题考查的是新定义情境下的有理数的加减乘除运算，弄懂新定义的含义是解题的关键．根据新定义的运算法则进行计算即可得到答案．
【详解】解：根据题意，得，
故选：B．
40．（23-24七年级上·江苏苏州·阶段练习）用“*”定义一种新运算：对于任何有理数a和b，规定，如，则的值为（ ）
A．B．8C．4D．
【答案】D
【分析】本题考查了新定义下的有理数运算，根据给出的新定义进行计算即可，按照新定义准确计算是解题的关键．
【详解】解：根据，
可得，
故选：D．
41．（23-24七年级上·江西吉安·阶段练习）定义新运算：当时，；当时，（其中）．则 ．
【答案】
【分析】本题考查了有理数的混合运算，理解定义的新运算是解题的关键．
按照定义的新运算进行计算，即可解答．
【详解】解：由题意得：
故答案为：．
42．（23-24七年级上·浙江温州·阶段练习）定义一种新运算“”，规则为：例：，则 ．
【答案】4
【分析】此题主要考查了新定义以及有理数的混合运算，正确利用新定义转化为有理数混合运算是解题关键．
根据题中的新定义将所求式子化为有理数混合运算，计算即可．
【详解】，
，
，
，
；
故答案为：4
43．（23-24七年级上·陕西咸阳·阶段练习）对于有理数定义运算：，如，则的结果为 ．
【答案】10
【分析】此题考查了有理数的混合运算，根据新定义的运算代入数值进行计算即可，熟练掌握有理数的运算法则和顺序是解题的关键．
【详解】解：∵，
∴，
故答案为：10
44．（23-24七年级上·重庆沙坪坝·期中）若定义一种新的运算，则下列结论：①；②；③．上述结论正确的有（写出番号） ．
【答案】①②/②①
【分析】本题考查了有理数的混合运算及整式的运算，根据新定义列出算式是解题的关键．根据新定义运算依次计算每个式子即可求解．
【详解】解：依题意得：，故①正确，
，
，故②正确，
，
,
∴，故③错误，
则结论正确的有①②，
故答案为：①②．
45．（23-24七年级上·广东东莞·阶段练习）我们定义一种新运算：．例如：．
(1)求的值；
(2)求的值．
【答案】(1)
(2)
【分析】本题主要考查了新定义，含乘方的有理数混合计算：
（1）根据新定义得到，据此代值计算即可；
（2）根据（1）所求得到，再根据，进行计算求解即可．
【详解】（1）解：由题意得：
；
（2）解：
．
46．（23-24七年级上·河南安阳·阶段练习）对于有理数，，都不为定义运算：．例如，．
(1)求的值；
(2)求的值．
【答案】(1)
(2)
【分析】本题考查的是新定义运算，有理数的四则混合运算；
（1）根据新定义进行计算即可求解；
（2）根据新定义先计算，再根据进行计算即可求解．
【详解】（1）解：，
．
（2），
，
．
47．（23-24七年级上·山东烟台·期末）定义新运算“”如下：当时（“”是指大于或等于），；当时，．
(1)求的值；
(2)求的值；
(3)若，求的值．
【答案】(1)的值为20
(2)的值为
(3)x的值为7
【分析】本题考查定义新运算，有理数的运算，解一元一次方程．掌握新运算的法则，是解题的关键．
（1）根据新运算的法则，列出算式，计算即可；
（2）根据新运算的法则，列出算式，计算即可；
（3）根据新运算的法则，列出方程，进行求解即可．
【详解】（1）解：因为，
所以，
所以，
所以的值为20；
（2）因为，
所以，
所以
所以的值为．
（3）当时，即为：，解之得；
当时，即为：，解之得，不合题意，舍去
所以，x的值为7．
乘方运算
…
…
新运算
…
…