

2023-2024学年山东省淄博市高二下学期期末考试数学试题(含答案)
展开一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.设等差数列{an},a2=3,d=5,则a5=( )
A. −5B. 18C. 23D. 28
2.若函数f(x)满足limΔx→0f(1−Δx)−f(1)Δx=18,则f′(1)=( )
A. −18B. −14C. 18D. 14
3.设{an}是等比数列,且a2+a3=2,a5+a6=−16,则公比q=( )
A. −2B. 2C. −8D. 8
4.在(2− x)7的展开式中,含x2的项的系数为( )
A. −280B. 280C. −560D. 560
5.某志愿者小组有5人,从中选3人到A、B两个社区开展活动,其中1人到A社区,则不同的选法有( )
A. 12种B. 24种C. 30种D. 60种
6.直线y=kx与曲线y=ln2x相切,则实数k的值为( )
A. 1B. 12C. 2eD. 2e2
7.若P(B|A)=13,P(A)=34,P(B)=12,则P(A|B)=( )
A. 14B. 34C. 13D. 12
8.不等式2lnx> xln2的解集是( )
A. (1,2)B. (4,+∞)C. (2,+∞)D. (2,4)
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.已知随机变量X~N(3,1),则下列说法正确的是( )
A. 若Y=X+3,则E(Y)=6B. 若Y=3X+1,则D(Y)=3
C. P(X≤2)=P(X≥4)D. P(0≤X≤4)=1-2P(X≥4)
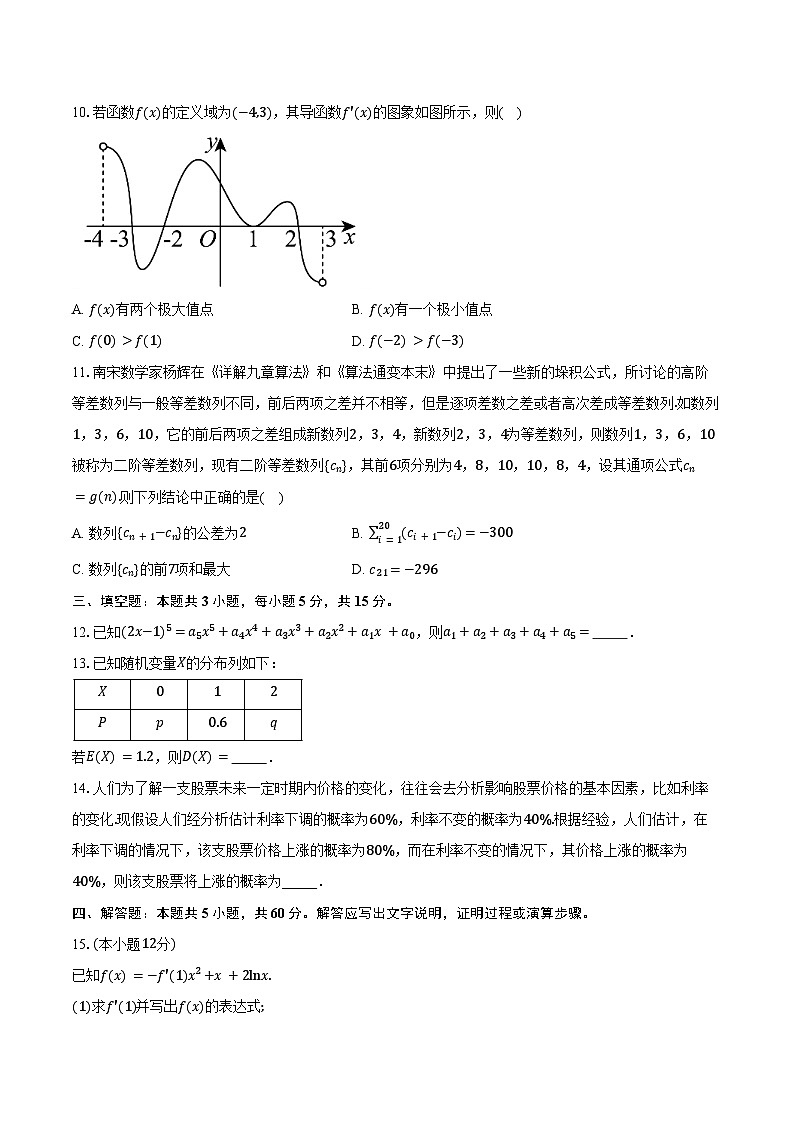
10.若函数f(x)的定义域为(−4,3),其导函数f′(x)的图象如图所示,则( )
A. f(x)有两个极大值点B. f(x)有一个极小值点
C. f(0)>f(1)D. f(−2)>f(−3)
11.南宋数学家杨辉在《详解九章算法》和《算法通变本末》中提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列.如数列1,3,6,10,它的前后两项之差组成新数列2,3,4,新数列2,3,4为等差数列,则数列1,3,6,10被称为二阶等差数列,现有二阶等差数列{cn},其前6项分别为4,8,10,10,8,4,设其通项公式cn=g(n).则下列结论中正确的是( )
A. 数列{cn+1−cn}的公差为2B. i=120(ci+1−ci)=−300
C. 数列{cn}的前7项和最大D. c21=−296
三、填空题:本题共3小题,每小题5分,共15分。
12.已知(2x−1)5=a5x5+a4x4+a3x3+a2x2+a1x+a0,则a1+a2+a3+a4+a5= .
13.已知随机变量X的分布列如下:
若E(X)=1.2,则D(X)= .
14.人们为了解一支股票未来一定时期内价格的变化,往往会去分析影响股票价格的基本因素,比如利率的变化.现假设人们经分析估计利率下调的概率为60%,利率不变的概率为40%.根据经验,人们估计,在利率下调的情况下,该支股票价格上涨的概率为80%,而在利率不变的情况下,其价格上涨的概率为40%,则该支股票将上涨的概率为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
已知f(x)=−f′(1)x2+x+2lnx.
(1)求f′(1)并写出f(x)的表达式;
(2)证明:f(x)≤x−1.
16.(本小题12分)
近年来,养宠物的人越来越多,在供需端及资本的共同推动下中国宠物经济产业迅速增长,数据显示,目前中国养宠户数在全国户数中占比为15.
(1)随机抽取200名成年人,并调查这200名成年人养宠物的情况,统计后得到如下列联表:
依据小概率值α=0.01的独立性检验,判断能否认为养宠物与性别有关?
(2)记2018−2023年的年份代码x依次为1,2,3,4,5,6,中国宠物经济产业年规模为y (单位:亿元),由这6年中国宠物经济产业年规模数据求得y,关于x的回归方程为y=0.86x+0.63,且 i=16(yi−y)2≈3.61.求相关系数r,并判断该回归方程是否有价值.
参考公式及数据:χ2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d),其中n=a+b+c+d
回归方程y=bx+a,其中b=i=1n(xi−x)(yi−y)i=1n(xi−x)2,a=y−bx,相关系数r=i=1n(xi−x)(yi−y) i=1n(xi−x)2i=1n(yi−y)2;若|r|≥0.75,则认为y与x有较强的相关性.其中 17.5≈4.18.
17.(本小题12分)
在一个不透明的密闭纸箱中装有10个大小、形状完全相同的小球,其中8个白球,2个黑球.小张每次从纸箱中随机摸出一个小球观察其颜色,连续摸4次,记随机变量X为小张摸出白球的个数.
(1)若小张每次从纸箱中随机摸出一个小球后放回纸箱,求E(X)和D(X);
(2)若小张每次从纸箱中随机摸出一个小球后不放回纸箱,求X的分布列.
18.(本小题12分)
已知数列{an}的前n项和为Sn,且Sn满足lg2(Sn+2)=n+1.
(1)求数列{an}的通项公式;
(2)数列{bn}的通项bn=n,求{an⋅bn}的前n项和Mn;
(3)在任意相邻两项ak与ak+1(其中k∈N∗)之间插入2k个3,使它们和原数列的项构成一个新的数列{cn}.记Tn为数列{cn}的前n项和,求T36的值.
19.(本小题12分)
已知函数f(x)=aln(x+2)−12x2(a∈R).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)有两个极值点,
(i)求实数a的取值范围;
(ii)证明:函数f(x)有且只有一个零点.
参考答案
1.B
2.A
3.A
4.B
5.C
6.C
7.D
8.D
9.AC
10.AB
11.BD
12.2
14.64%
15.解:(1)因为f′(x)=−2f′(1)x+1+2x,令x=1解得f′(1)=1,所以f(x)=−x2+x+2lnx.
(2)构造F(x)=f(x)−x+1=−x2+2lnx+1,F′(x)=−2x+2x=2(1−x)(1+x)x.
当0
当x≥1时,F′(x)≤0,于是F(x)在[1,+∞)单调递减,
所以Fmax(x)=F(1)=0,于是F(x)≤F(1)=0,所以f(x)≤x−1.
16.解:(1)因为χ2=200×38×40−62×602100×100×102×98≈9.684>6.635,
依据小概率值α=0.01的独立性检验,可以认为是否养宠物与性别有关联.
(2)由x的取值依次为1,2,3,4,5,6,得x=3.5,i=16xi−x2=17.5,
因为回归方程为y=0.86x+0.63,
所以b=i=16xi−xyi−yi=16xi−x2=i=16xi−xyi−y17.5=0.86,
所以i=16xi−xyi−y=15.05,
所以r=i=16xi−xyi−y i=16xi−x2i=16yi−y2≈×3.61≈0.997.
因为r>0.75,所以y与x有较强的相关性,该同归方程有价值.
17.解:(1)由已知得,X~B(4,0.8),
所以E(X)=4×0.8=3.2,
D(X)=4×0.8×(1-0.8)=0.64.
(2)由已知得,X服从超几何分布,
且P(X=k)=C8kC24−kC104,k=2,3,4,
P(X=2)=C82C24−2C104=215,
P(X=3)=C83C24−3C104=815,
P(X=4)=C84C24−4C104=13,
所以X的分布列为
18.解:(1)已知数列{an}的前n项和为Sn,且Sn满足lg2(Sn+2)=n+1,
则Sn+2=2n+1,
则当n≥2时,an=Sn−Sn−1=2n+1−2n=2n,
又a1=22−2=2满足上式,
即数列{an}的通项公式为an=2n;
(2)由(1)可知an⋅bn=n×2n,
所以Mn=1×2+2×22+3×23+⋯+n×2n,
所以2Mn=1×22+2×23+3×24+⋯+n×2n+1,
则−Mn=1×2+1×22+1×23+⋯+1×2n−n×2n+1
=2(1−2n)1−2−n×2n+1=(1−n)×2n+1−2,
所以Mn=(n−1)×2n+1+2;
(3)在任意相邻两项ak与ak+1(其中k∈N∗)之间插入2k个3,
使它们和原数列的项构成一个新的数列{bn},
则a5为数列{bn}的第21+22+23+24+5=34项,
则b35=b36=3,
则T36=31×3+a1+a2+a3+a4+a5=93+2×(1−25)1−2=155.
19.解:(1)因为f′(x)=ax+2−x=−(x+1)2+a+1x+2,
(i)当a≤−1时,f(x)在(−2,+∞)单调递减;
(ii)当−1
当x∈(− a+1−1, a+1−1),f′(x)>0.
当x∈( a+1−1,+∞),f′(x)<0.
所以f(x)在(−2,− a+1−1)单调递减,在(− a+1−1, a+1−1)单调递增,在( a+1−1,+∞)单调递减;
(iii)当a≥0时,f(x)在(−2, a+1−1)单调递增,( a+1−1,+∞)单调递减.
(2) (i)由(1)知−1
因为f( a+1−1)=aln( a+1+1)−12( a+1−1)2<0,
又因为f(e4a−2)=4−12(e4a−2)2>0.
所以函数f(x)有且只有一个零点.X
0
1
2
P
p
0.6
q
成年男性
成年女性
合计
养宠物
38
60
98
不养宠物
62
40
102
合计
100
100
200
α
0.10
0.05
0.01
xα
2.706
3.841
6.635
X
2
3
4
P
215
815
13
山东省淄博市2023-2024学年高一下学期7月期末考试数学试题: 这是一份山东省淄博市2023-2024学年高一下学期7月期末考试数学试题,共4页。
山东省淄博市2023-2024学年高二下学期期末考试数学试题: 这是一份山东省淄博市2023-2024学年高二下学期期末考试数学试题,文件包含高二数学试题参考答案阅卷用docx、高二数学试题2024625pdf等2份试卷配套教学资源,其中试卷共10页, 欢迎下载使用。
山东省淄博市2023-2024学年度高二下学期期末数学试题: 这是一份山东省淄博市2023-2024学年度高二下学期期末数学试题,共4页。试卷主要包含了 在的展开式中,含的项的系数为, 若则, 不等式的解集是等内容,欢迎下载使用。












