2023-2024学年辽宁省抚顺市新宾县八年级（下）期末数学试卷（含解析）

这是一份2023-2024学年辽宁省抚顺市新宾县八年级（下）期末数学试卷（含解析），共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.二次根式 2x−3有意义时，x的取值范围是( )
A. x≤32B. x<32C. x>32D. x≥32
2.计算(1+ 2)2024(1− 2)2023的结果是( )
A. 2−1B. −1C. 1D. −1− 2
3.高速公路是指专供汽车高速行驶的公路.高速公路在建设过程中，通常要从大山中开挖隧道穿过，把道路取直以缩短路程.其中的数学原理是( )
A. 两点之间，线段最短
B. 两点确定一条直线
C. 平行线之间的距离最短
D. 垂线段最短
4.已知一次函数y=−2x+4的图象经过点(2,a)，则a的值为( )
A. 8B. −1C. 1D. 0
5.一组数据2，−5，0，2，−4，3，的中位数和众数分别是( )
A. 0，2B. 2，2C. 1，3D. 1，2
6.下表记录了甲、乙、丙、丁四名同学最近几次数学课堂检测成绩的平均数与方差.数学老师准备奖励其中一名成绩好且发挥稳定的同学，应该选择 ( )
A. 甲B. 乙C. 丙D. 丁
7.如图，在▱ABCD中，已知AD=8cm，AB=5cm，DE平分∠ADC交BC边于点E，则BE等于( )
A. 1cm
B. 2cm
C. 3cm
D. 4cm
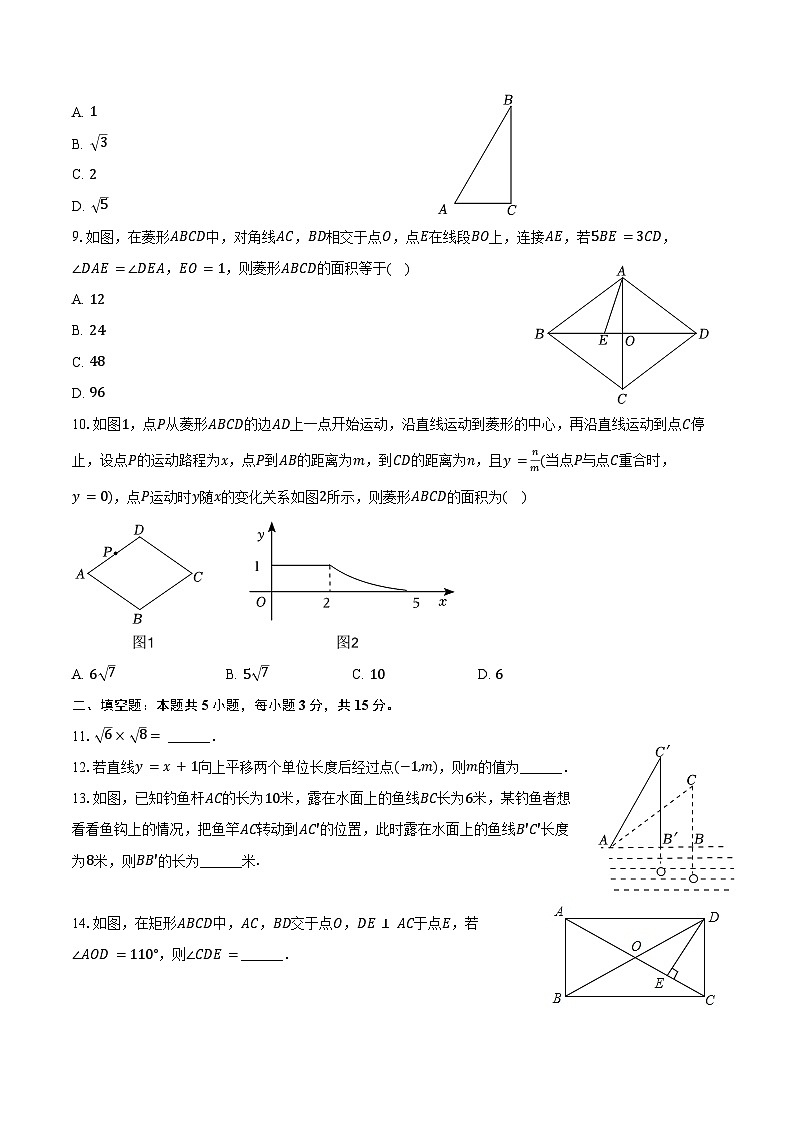
8.如图，在△ABC中，∠C=90°，若AC=1，AB=2，则BC的长是( )
A. 1
B. 3
C. 2
D. 5
9.如图，在菱形ABCD中，对角线AC，BD相交于点O，点E在线段BO上，连接AE，若5BE=3CD，∠DAE=∠DEA，EO=1，则菱形ABCD的面积等于( )
A. 12
B. 24
C. 48
D. 96
10.如图1，点P从菱形ABCD的边AD上一点开始运动，沿直线运动到菱形的中心，再沿直线运动到点C停止，设点P的运动路程为x，点P到AB的距离为m，到CD的距离为n，且y=nm(当点P与点C重合时，y=0)，点P运动时y随x的变化关系如图2所示，则菱形ABCD的面积为( )
A. 6 7B. 5 7C. 10D. 6
二、填空题：本题共5小题，每小题3分，共15分。
11. 6× 8= ______．
12.若直线y=x+1向上平移两个单位长度后经过点(−1,m)，则m的值为______．
13.如图，已知钓鱼杆AC的长为10米，露在水面上的鱼线BC长为6米，某钓鱼者想看看鱼钩上的情况，把鱼竿AC转动到AC′的位置，此时露在水面上的鱼线B′C′长度为8米，则BB′的长为______米.
14.如图，在矩形ABCD中，AC，BD交于点O，DE⊥AC于点E，若∠AOD=110°，则∠CDE=______．
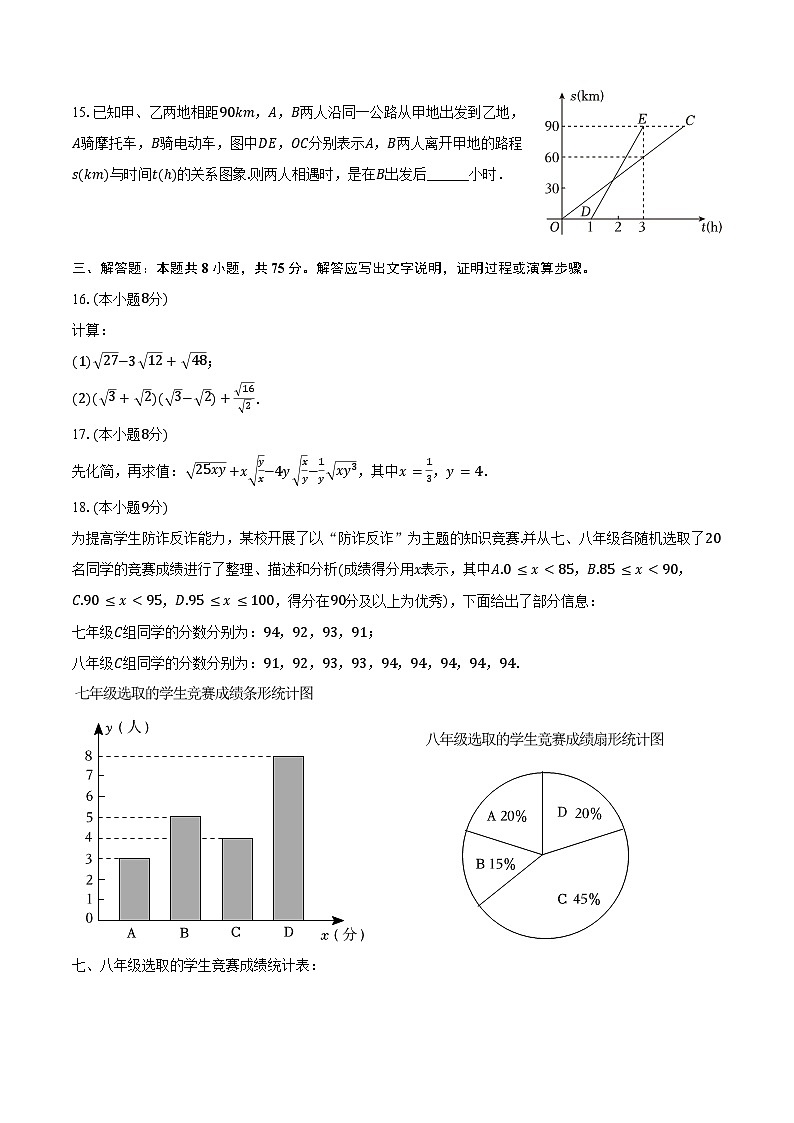
15.已知甲、乙两地相距90km，A，B两人沿同一公路从甲地出发到乙地，A骑摩托车，B骑电动车，图中DE，OC分别表示A，B两人离开甲地的路程s(km)与时间t(ℎ)的关系图象.则两人相遇时，是在B出发后______小时．
三、解答题：本题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题8分)
计算：
(1) 27−3 12+ 48；
(2)( 3+ 2)( 3− 2)+ 16 2．
17.(本小题8分)
先化简，再求值： 25xy+x yx−4y xy−1y xy3，其中x=13，y=4．
18.(本小题9分)
为提高学生防诈反诈能力，某校开展了以“防诈反诈”为主题的知识竞赛.并从七、八年级各随机选取了20名同学的竞赛成绩进行了整理、描述和分析(成绩得分用x表示，其中A.0≤x<85，B.85≤x<90，C.90≤x<95，D.95≤x≤100，得分在90分及以上为优秀)，下面给出了部分信息：
七年级C组同学的分数分别为：94，92，93，91；
八年级C组同学的分数分别为：91，92，93，93，94，94，94，94，94．

七、八年级选取的学生竞赛成绩统计表：
请根据以上信息，完成下列问题：
(1)填空：a= ______，b= ______，m= ______；
(2)根据以上数据，你认为该校七、八年级学生在”防诈反诈”知识竞赛中，哪个年级学生对“防诈反诈”的了解情况更好？请说明理由；(写出一条理由即可)
(3)该校现有七年级学生500名，请估计七年级竞赛成绩为优秀的学生人数．
19.(本小题8分)
港珠澳大乔是一座连接香港，广东珠海和澳门的跨海大桥，总长55km，现有一艘游轮即将靠岸，当游轮到达B点后熄灭发动机，在离水面高度为5m的岸上，工作人员用绳子牵引靠岸，开始时绳子BC的长为13m.(假设绳子是直的，结果保留根号)
(1)若工作人员以1.5m/s的速度收绳.4s后船移动到点D的位置，问此时游轮距离岸边还有多少m？
(2)若游轮熄灭发动机后保持0.8m/s的速度匀速靠岸，10s后船移动到E点，工作人员手中的绳子被收上来多少米？
20.(本小题8分)
如图，在△ABC中，AB=AC，D是BC的中点，点E，F在射线AD上，且DE=DF．
(1)求证：四边形BECF是菱形；
(2)若AD=BC=8，AE=BE，求菱形BECF的面积．
21.(本小题10分)
有一块矩形木板，木工师傅采用如图所示的方式，在木板上截出面积分别为18dm2和32dm2的两块正方形木板．
(1)截出的两块正方形木板的边长分别为______dm，______dm；
(2)求剩余木板的面积；
(3)如果木工师傅想从剩余的木板中截出长为1.5dm、宽为1dm的矩形木条，最多能截出______个这样的木条．
22.(本小题12分)
鲜花是云南的名片，更是云南送给世界的礼物.在日新月异的技术加持下，云南鲜花为各地带去了来自高原的芬芳与绚烂.元日前夕，某批发商购进A、B两种类型的玫瑰花共100束，其中A种类型的玫瑰花价格为每束25元，购买B种类型的玫瑰花所需费用y(单位：元)与购买数量x(单位：束)的函数关系图象如图所示．
(1)求y与x的函数关系式；
(2)若购买B种类型玫瑰花所需的数量不超过60束，但不少于A种类型玫瑰花的数量，试问如何购买能使购买费用最少，并求出最少费用．
23.(本小题12分)
如图，在平面直角坐标系中，正方形ABCD的顶点A、B分别在y轴正半轴、x轴正半轴上，过点D作DF⊥x轴交x轴于点F，交对角线AC于点E．
(1)求证：BE=DE；
(2)判断∠EBC、∠FBC的数量关系，并说明理由；
(3)若点A，B坐标分别为(0,12)、(5,0)，则△BEF的周长为______．
答案简析
1.D
【简析】解：根据题意得：2x−3≥0，
解得：x≥32．
故选：D．
2.D
【简析】解：原式=[(1+ 2)(1− 2)]2023×(1+ 2)
=(1−2)2023×(1+ 2)
=(−1)2023×(1+ 2)
=−(1+ 2)
=−1− 2．
故选：D．
3.A
【简析】解：在高速公路的建设中，通常从大山中开挖隧道穿过，把道路取直，以缩短路程，
这是因为：两点之间，线段最短．
故选：A．
4.D
【简析】解：∵一次函数y=−2x+4的图象经过点(2,a)，
∴a=−2×2+4，
解得：a=0，
∴a的值为0．
故选：D．
5.D
【简析】解：一组数据2，−5，0，2，−4，3，
从小到大排列为：−5，−4，0，2，2，3，
中位数为：0+22=1，众数为：2，
故选：D．
6.B
【简析】解：∵乙、丙、丁的平均数相同且比甲大，
∴从乙、丙、丁中选择一人参加竞赛，
∵乙、丙、丁的方差中乙的最小，
∴奖励乙；
故选：B．
7.C
【简析】解：∵四边形ABCD是平行四边形，AD=8cm，AB=5cm，
∴AD=BC=8cm，AB=CD=5cm，AD//BC，
∴∠ADE=∠DEC，
∵E平分∠ADC，
∴∠ADE=∠EDC，
∴∠EDC=∠DEC，
∴CE=DC=5cm，
∴BE=BC−CE=3cm，
故选：C．
8.B
【简析】解：∵∠C=90°，AC=1，AB=2，
∴BC= AB2−AC2= 22−12= 3，
即BC的长是 3，
故选：B．
9.B
【简析】解：∵5BE=3CD，
∴BECD=35，
设BE=3x，CD=5x，
∵四边形ABCD为菱形，
∴AB=AD=CD=5x，OB=OD，OA=OC，AC⊥BD，
∵EO=1，
∴BO=OD=3x+1，DE=OD+OE=3x+2，
∵∠DAE=∠DEA，
∴AD=DE=3x+2，
∴5x=3x+2，
解得x=1，
∴AB=AD=5，OB=OD=4，BD=2OD=8，
∴AO= AB2−OB2=3，
∴AC=2AO=6，
∴菱形ABCD的面积等于12BD×AC=24．
故选：B．
10.A
【简析】解：连接AC，BD交于点O，连接OP，如图，
由题意知，当0≤x≤2时，y的值恒等于1，
∴m=n．
∴点P的运动路径是△ADC的中位线，且CD=2×2=4．
∵当x=5时，y=0，
∴OC=3．
由菱形的性质可得AC=2OC，BD=2OD，AC⊥BD，
∴AC=2OC=6，
∴OD= CD2−OC2= 7．
∴BD=2OD=2 7．
∴S菱形ABCD=12BD⋅AC=12×2 7×6=6 7，
故选：A．
11.4 3
【简析】解：原式= 6×8=4 3．
故答案为：4 3．
12.2
【简析】解：由题意，平移后的简析式为：y=x+1+2=x+3，
把(−1,m)代入得：m=−1+3=2，
故答案为：2．
13.2
【简析】解：在Rt△ABC中，AC=10m，BC=6m，
∴AB= AC2−BC2= 102−62=8(m)，
在Rt△AB′C′中，AC′=10m，B′C′=8m，
∴AB′= AC′2−B′C′2= 102−82=6(m)，
∴BB′=AB−AB′=8−6=2(m)；
故答案为：2．
14.35°
【简析】解：∵四边形ABCD是矩形，
∴∠ADC=90°，AC=BD，OA=OC，OB=OD，
∴OC=OD，
∴∠ODC=∠OCD，
∵∠AOD=110°，
∴∠DOE=70°，∠ODC=∠OCD=12(180°−70°)=55°，
∵DE⊥AC，
∴∠ODE=90°−∠DOE=20°，
∴∠CDE=∠ODC−∠ODE=55°−20°=35°．
故答案为：35°．
15.1.8
【简析】解：由图象可得，
A的速度为：90÷(3−1)=45(km/ℎ)，
B的速度为：60÷3=20(km/ℎ)，
设两人相遇时，是在B出发后m小时，
由题意可得：20m=45(m−1)，
解得m=1.8，
即两人相遇时，是在B出发后1.8小时，
故答案为：1.8．
16.解：(1)原式=3 3−6 3+4 3
= 3；
(2)原式=3−2+ 162
=1+2 2．
【简析】(1)先把各二次根式化为最简二次根式，然后合并即可；
(2)根据平方差公式和二次根式的除法法则运算即可．
17.解：∵x=13>0，y=4>0，
∴原式=5 xy+ xy−4 xy− xy
= xy，
当x=13，y=4时，原式= 13×4=2 33．
【简析】先把各二次根式化为最简二次根式，再合并得到原式= xy，然后把x、y的值代入计算．
18.92.5 94 60%
【简析】解：(1)由条形统计图可知：A组人数是3名，B组人数是5名，C组人数是4名，
所以七年学生成绩按从小到大排列，第10名，第11名是92，93，
所以七年学生成绩的中位数a=92+932=92.5；
八年级A组人数为：20×20%=4(名)，
B组人数为：20×15%=3(名)，
C组人数为：20×45%=9(名)
D 组人数为：20×20%=4(名)，
而八年级C组同学的分数中94的人数是5名，都要比其它组总人数都要多，
所以八年级学生成绩的众数是94，即b=94；
m=4+820×100%=60%．
故答案为：92.5；94；60%．
(2)八年级学生对国家安全的了解情况更好．
理由：从平均数看两个年级相同，从中位数看，八年级93比七年级92.5高，从优秀率看八年级65%比七年级60%大，所以八年级学生对国家安全的了解情况更好．
(3)500×4+820=300(名)，
答：估计七年级竞赛成绩为优秀的学生人数为300名．
19.解：(1)∵在Rt△ABC中，∠CAB=90°，BC=13m，AC=5m，
∴AB= 132−52=12，
∵此人以1.5m/s的速度收绳，4s后船移动到点D的位置，
∴CD=13−1.5×4=7(m)，
∴Rt△ACD中，AD= CD2−AC2= 49−25=2 6m，
∴游轮距离岸边还有2 6m；
(2)由题知，AE=AB−BE=12−0.8×10=4m，
∴CE= AC2+AE2= 25+16= 41m，
∴绳子被收上来(13− 41)m．
【简析】(1)在Rt△ABC中，运用勾股定理算出AB=12，根据题意得出CD=13−1.5×4=7(m)，再在Rt△ACD中运用勾股定理即可求解；
(2)根据勾股定理算出CE即可求解．
20.(1)证明：∵AB=AC，D是BC的中点，
∴BD=CD，AD⊥BC，
∵DE=DF，
∴四边形BECF是菱形；
(2)解：设DE=x，
∵AD=BC=8，AE=BE，BD=CD，
∴AE=BE=8−x，BD=4，
∵AD⊥BC，
∴∠BDE=90°，
在Rt△BDE中，BD2+DE2=BE2，
即42+x2=(8−x)2，
解得x=3，
∴DE=3，则EF=6，
∴菱形BECF的面积=12⋅BC⋅EF=12×8×6=24．
【简析】(1)先由等腰三角形“三线合一”的性质得到BD=CD，AD⊥BC，再结合“对角线相互垂直的平行四边形是菱形”即可证明结论；
(2)设DE=x，根据题意，表示出AE=BE=8−x，BD=4，再根据勾股定理列出方程求解，最后计算菱形的面积即可．
21.3 2 4 2 2
【简析】解：(1)根据题意得：截出的两块正方形木料的边长分别为 18=3 2dm， 32=4 2dm，
故答案为：3 2，4 2；
(2)根据题意得：矩形的长为3 2+4 2=7 2(dm)，宽为4 2dm，
∴剩余木板的面积=(7 2×4 2)−18−32=6(dm2)；
(3)根据题意得：从剩余的木料的长为3 2dm，宽为4 2−3 2= 2(dm)，
∵3 2<3×1.5， 2>1，
∴能截出2×1=2块这样的木条．
故答案为：2．
22.解：(1)由图知：当0≤x<10时，y=20x，
当x≥10时，设y与x的函数关系式为y=kx+b(k≠0)，
它的图象经过点(10,200)与点(20,360)，
∴10k+b=20020k+b=360，
解这个方程组得k=16b=40，
∴y与x的函数关系式为y=20x,0≤x<1016x+40,x≥10；
(2)设购买B种类型玫瑰花的数量为m束，则A种类型的玫瑰花的数量为(100−m)束，总费用为w元，
由题知：m≤60且m≥100−m，解得50≤m≤60，
∴w=25(100−m)+16m+40=−9m+2540，
∵−9<0，
∴w随m的增大而减小，
∵50≤m≤60，
∴当m=60时，w有最小值为2000元；
此时，A种类型的玫瑰花：100−60=40(束)，
答：购买A种类型的玫瑰花40束，购买B种类型的玫瑰花60束时，购买费用最少，最少费用为2000元．
【简析】(1)根据函数图象中的数据可以求得y与x之间的函数简析式；
(2)设费用为W，根据题意可以得到W与B种类型玫瑰花的函数关系，再根据购买B种类型玫瑰花所需的数量不超过60束，但不少于A种类型玫瑰花的数量，可以求得B种类型玫瑰花的数量的取值范围，然后根据一次函数的性质即可解答本题．
23.24
【简析】(1)证明：∵四边形ABCD是正方形，
∴AD=AB，∠DAE=∠BAE，
在△ADE与△ABE中，
AD=AB∠DAE=∠BAEAE=AE，
∴△ADE≌△ABE(SAS)
∴BE=DE；
(2)解：∠EBC=∠FBC，理由如下：
如图所示，设BC，DF交于点H，
∵DF⊥x轴，∠DCH=90°
∴∠HFB=∠DCH，
又∵∠DHC=∠BHF，
∴∠CBF=∠CDF，
∵△ADE≌△ABE
∴∠ADE=∠ABE，
又∵∠ADC=∠ABC=90°，
∴∠ADC−∠ADE=∠ABC−∠ABE，即∠EBC=∠EDC，
∴∠EBC=∠FBC；
(3)解：如图所示，过点D作DG⊥y轴于点G，
则四边形OGDF是矩形，
∵四边形ABCD是正方形，
∴AD=AB，∠BAD=90°，
∵∠DGA=∠AOB=90°，
∴∠BAO=90°−∠GAD=∠ADG，
∴△BAO≌△ADG(AAS)，
∴GD=AO，AG=OB，
∵点A，B坐标分别为(0,12)、(5,0)，
∴OA=GD=12，AG=OB=5，
∴DF=OG=12+5=17，BF=OF−BO=GD−OB=12−5=7，
∵BE=DE，
∴△BEF的周长为BE+EF+BF=DE+EF+BF=DF+BF=17+7=24．
故答案为：24．甲
乙
丙
丁
平均数(分)
92
95
95
95
方差
3.6
3.6
7.4
8.1
年级
平均数
中位数
众数
优秀率
七
91
a
95
m
八
91
93
b
65%