



初中数学北师大版八年级上册1 探索勾股定理备课ppt课件
展开
这是一份初中数学北师大版八年级上册1 探索勾股定理备课ppt课件,共23页。
1. 在Rt△ ABC 中,已知两直角边的长分别为3和4,则△ ABC 的
周长为( B )
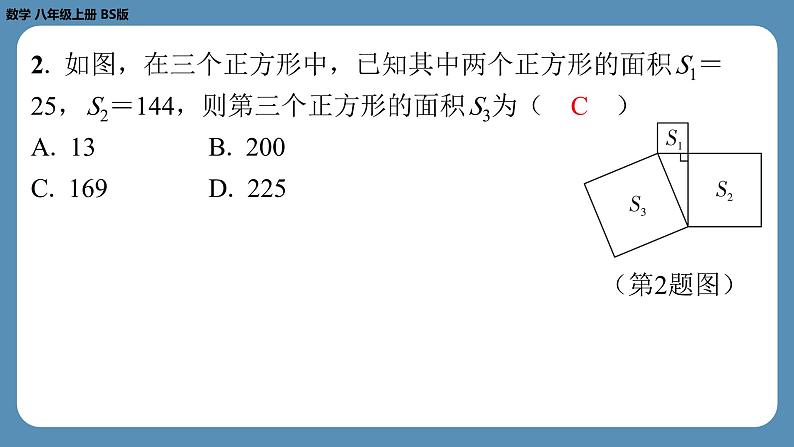
2. 如图,在三个正方形中,已知其中两个正方形的面积 S1=
25, S2=144,则第三个正方形的面积 S3为( C )
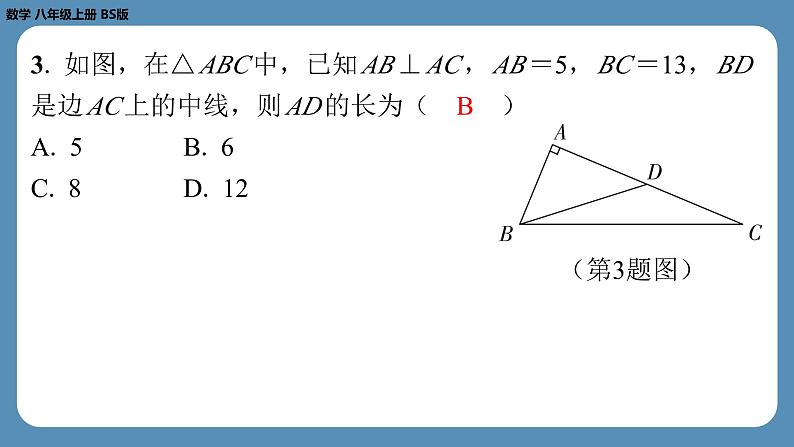
3. 如图,在△ ABC 中,已知 AB ⊥ AC , AB =5, BC =13, BD
是边 AC 上的中线,则 AD 的长为( B )
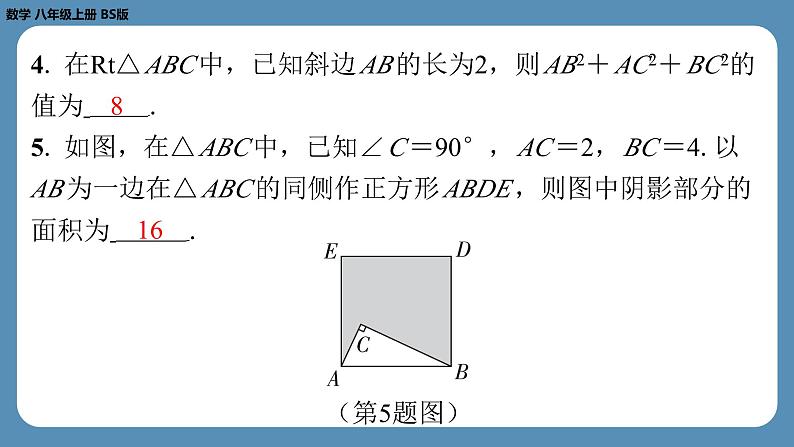
4. 在Rt△ ABC 中,已知斜边 AB 的长为2,则 AB2+ AC2+ BC2的
值为 .5. 如图,在△ ABC 中,已知∠ C =90°, AC =2, BC =4.以
AB 为一边在△ ABC 的同侧作正方形 ABDE ,则图中阴影部分的
面积为 .
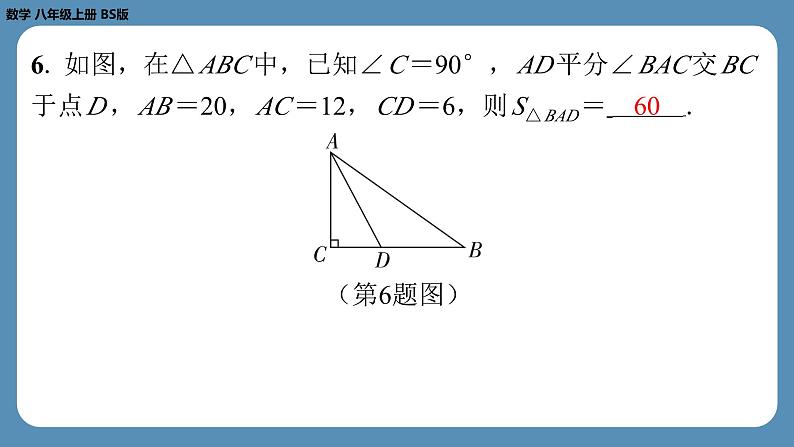
6. 如图,在△ ABC 中,已知∠ C =90°, AD 平分∠ BAC 交 BC
于点 D , AB =20, AC =12, CD =6,则 S△ BAD = .
7. 如图,在Rt△ ABC 中,已知∠ ACB =90°,∠ A ,∠ B ,∠ ACB 所对的边的长分别为 a , b , c , CD 是边 AB 上的高.(1)若 a ∶ b =3∶4, c =15,求 b 的值;(2)若 a =6, b =8,求 c 的值及 CD 的长.
解:(1)设 a =3 x ,则 b =4 x .在Rt△ ABC 中,根据勾股定理,得 a2+ b2= c2.所以(3 x )2+(4 x )2=152.
解得 x =3(负值舍去).所以 b =4 x =4×3=12.
8. 如图,在四边形 ABCD 中,已知 AB =4, AD =3, AB ⊥
AD , BC =12,连接 BD . (1)求 BD 的长;(2)若△ BDC 是以 CD 为斜边的直角三角形,求 CD 的长.
解:(1)因为 AB =4, AD =3, AB ⊥ AD ,所以 BD2= AD2+ AB2=32+42=25.所以 BD =5(负值舍去),即 BD 的长是5.
(2)在Rt△ BCD 中, BD =5, BC =12.因为 CD 为斜边,所以 CD2= BD2+ BC2=52+122=169.所以 CD =13(负值舍去),即 CD 的长是13.
9. 已知一个直角三角形的周长为24,斜边长为10,则该直角三
角形的面积为 .
10. 如图,在Rt△ ABC 中,已知∠ A =90°, BC =10, AB =6.
若动点 P 在 AC 边上,且点 P 到△ ABC 的两个顶点的距离相等,
则 PA 的长为 .
【解析】在Rt△ ABC 中, 因为∠ A =90°, BC =10, AB =6,
所以 AC2= BC2- AB2=102-62=64.所以 AC =8(负值舍去).
11. 如图,把一张长为8,宽为4的长方形纸片 ABCD 沿 EF 折叠
起来,使其对角顶点 C 与点 A 重合,点 D 落在点 G 处.(1)求 DE 的长;(2)连接 DG ,求△ GED (阴影部分)的面积.
解:(1)由题意和折叠的性质,得 DE = GE , AG = CD =4,
∠ AGE =∠ CDA =90°.设 DE = GE = x ,则 AE =8- x .在Rt△ AEG 中, AG2+ GE2= AE2,即42+ x2=(8- x )2,解得 x =3.所以 DE =3.
12. 如图,在△ ABF 中,已知点 E 是边 AF 的中点,点 C 在边 BF
上,作 AD ∥ BF ,交 CE 的延长线于点 D . (1)试说明:△ ADE ≌△ FCE ;
(2)若∠ CEF =90°, AD =5, CE =4,求点 E 到 BF 的距离.
13. (选做)如图,这是一组美丽的“勾股树”,其中所有的
四边形都是正方形,所有的三角形都是直角三角形.(1)若图1、图2中正方形 A 的面积是100,则图1中正方形 B 和
正方形 C 的面积和是 .图2中正方形 D 、正方形 E 、正方
形 F 和正方形 G 的面积和是 ;
(2)若图3中正方形 A 的面积是160,则正方形 H 、正方形 I 、
正方形 J 、正方形 K 、正方形 L 、正方形 M 、正方形 N 和正方形
O 的面积和是多少?(3)如图2,若正方形 D , E , F , G 的边长分别是4,4,1,
2,则正方形 A 的面积是多少?
(1)【解析】因为题图1中的三角形是直角三角形,所以根据
勾股定理,得 S正方形 B + S正方形 C = S正方形 A . 又因为 S正方形 A =100,所以 S正方形 B + S正方形 C =100.同理,得题图2中,( S正方形 D + S正方形 E )+( S正方形 F + S正方形 G )= S正方形 B + S正方形 C = S正方形 A =100.故答案为100,100.
(2)解:在题图3中,根据勾股定理,得( S正方形 H + S正方形 I )+( S正方形 J + S正方形 K )+( S正方形 L + S正方
形 M )+( S正方形 N + S正方形 O )=( S正方形 D + S正方形 E )+( S正方
形 F + S正方形 G )= S正方形 B + S正方形 C = S正方形 A =160.
(3)解:根据勾股定理,得( S正方形 D + S正方形 E )+( S正方形 F + S正方形 G )= S正方形 B + S正方形C = S正方形 A ,所以 S正方形 A =42+42+12+22=16+16+1+4=37.
相关课件
这是一份初中数学北师大版七年级上册5.1 认识一元一次方程备课ppt课件,共23页。PPT课件主要包含了A级基础训练,B级能力训练,2x-16,C级拓展训练等内容,欢迎下载使用。
这是一份初中数学北师大版七年级上册第六章 数据的收集与整理6.3 数据的表示背景图课件ppt,共31页。PPT课件主要包含了A级基础训练,②③①,喜欢乒乓球情况统计图,B级能力训练,C级拓展训练等内容,欢迎下载使用。
这是一份北师大版七年级上册4.3 角授课课件ppt,共23页。PPT课件主要包含了A级基础训练,B级能力训练,C级拓展训练等内容,欢迎下载使用。









