

2025年高考数学一轮复习-第八章-立体几何初步、空间向量与立体几何【课件】
展开
这是一份2025年高考数学一轮复习-第八章-立体几何初步、空间向量与立体几何【课件】,共8页。
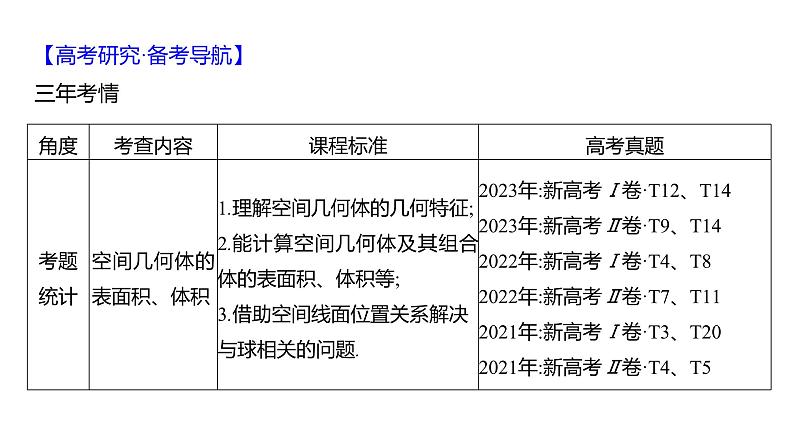
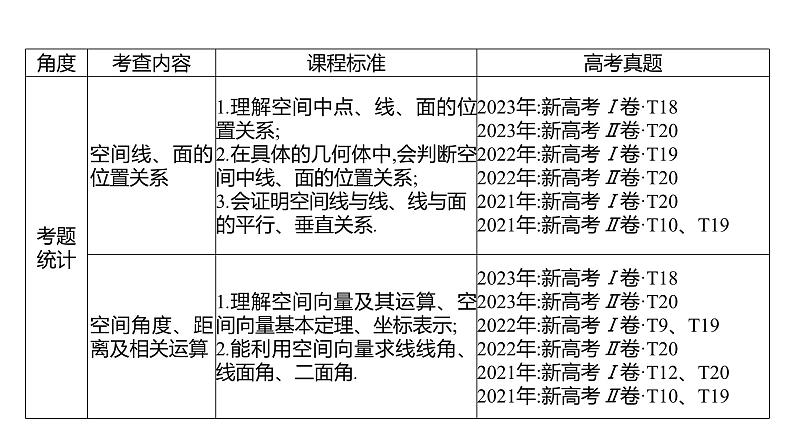
【高考研究·备考导航】三年考情
备考策略根据近3年新高考卷命题特点和规律,复习本章时,要注意以下几个方面:1.全面系统复习,深刻理解知识本质(1)掌握基本立体几何图形(柱体、锥体、台体和球及简单组合体)的结构特征、直观图、表面积、体积的计算公式,灵活运用折叠与展开、分割与补形、平面图形与立体图形的相互转化等方法,进行精准计算.会解决简单几何体与球的切接问题.(2)理解空间中点、线、面的位置关系,掌握直线、平面平行与垂直的定义、判定与性质定理,并能熟练运用.(3)掌握空间向量及其运算、空间向量基本定理;掌握空间角与空间距离的定义,并会用几何法和向量法求解.
2.熟练掌握解决下列问题的方法策略(1)直观图问题:经历识图、想图到构图的过程,想象出几何体的结构特征.(2)几何体的表面积和体积问题:熟记公式、运算无误,合理使用等积转换,割补思想.(3)直线与平面的平行、垂直关系的证明要培养分析法找思路、综合法写步骤的逻辑推理能力,运用判定定理和性质定理时要注意条件的完整性,面面垂直的性质定理要加强训练.(4)空间角和距离的求解既要掌握向量法也不能忽视几何法,牢记公式,特别是线面角的求解.
3.重视数学思想方法的应用(1)割补思想:在求体积、角和距离时,割补为特殊的几何体便于求解.(2)转化与化归思想:①点、线、面关系的相互转化;②空间向量与角、距离的相互转化;③点面距与体积的相互转化;④立体问题与平面问题相互转化;⑤生活实际问题与立体几何的转化.
相关课件
这是一份2025年高考数学一轮复习 第八章 -球的切、接、截面问题【课件】,共23页。PPT课件主要包含了梳理提炼,典例赏析,题型一外接球问题,题型二内切球问题,故选D,题型三截面问题等内容,欢迎下载使用。
这是一份2025届高考数学一轮复习 第八章 -球的切、接、截面问题课件,共23页。PPT课件主要包含了梳理提炼,典例赏析,题型一外接球问题,题型二内切球问题,故选D,题型三截面问题等内容,欢迎下载使用。
这是一份新高考数学一轮复习讲练测课件第7章必刷大题14空间向量与立体几何 (含解析),共48页。









