
河南省名校+安阳市第一中学2023-2024学年高二下学期7月期末考试数学试题
展开命题人:张冉 审核人:张书霞
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若集合A={x|2x<4},B={x∈N|−1
A.0.6B.0.5C.0.4D.0.3
3.已知函数f(x)={2x+2−x,x≤3f(x2),x>3,则f(lg29)=
A.83B.103C.809D.829
4.已知f(x)=csx(x2+3x)(x+a)为奇函数,则a=
A.3B.−3C.0D.−1
5.世界上海拔最高的天然“心形湖”位于四川省康定县的情歌木格措景区,被誉为藏在川西的“天空之心”.这个湖泊位于青藏高原,呈现出明亮的蓝绿色,水质清澈宛如明镜.湖泊周围环抱着雪山和梅花峰,景色优美迷人.下图1是这个“心形湖”,的轮廓,其形状如一颗爱心.图2是由此抽象出来的一个“心形”图形,这个图形可看作由两个函数的图象构成,则“心形”在x轴上方的图象对应的函数解析式可能为
A.y=|x|4−x2B.y=x4−x2C.y=−x2+2|x|D.y=−x2+2x
6.某班毕业晚会有唱歌、跳舞、小品、杂技、相声五个节目制成一个节目单.其中小品、相声不相邻且相声、跳舞相邻,这样的节目单有( )种
A.36B.40C.32D.42
7.已知定义在R上的函数f(x)满足f′(x)>2f(x),f(2)=e,则不等式f(x)>e2x−3的解集为
A.(−∞,2)B.(0,2)C.(2,+∞)D.(32,2)
8.若f(x)的定义域D为[0,+∞),f(0)=1,且对∀x∈D,满足f(x+2)−f(x)≤2x,f(x+4)−f(x)≥5⋅2x,则下列结论中,一定正确的是
A.f(10)>342B.f(10)=342C.f(12)>1366D.f(12)=1366
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列说法中,正确的是
A.命题“存在一个四边形,它的四个顶点不在同一个圆上”的否定是真命题.
B.命题“对∀x∈Z,x2的个位数不等于3”的否定是假命题.
C.梯形ABCD等腰梯形的充要条件是AC=BD.
D.设a,b,c∈R,则a2+b2+c2=ab+ac+bc的充要条件是a=b=c.
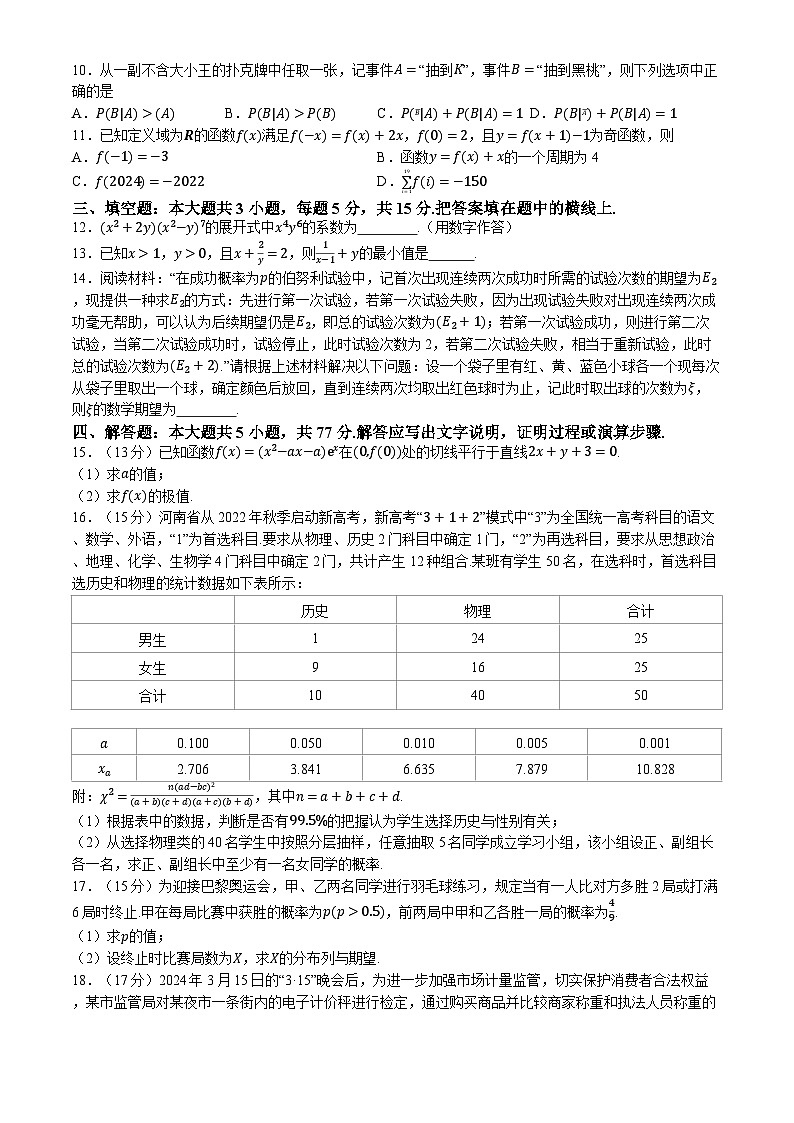
10.从一副不含大小王的扑克牌中任取一张,记事件A=“抽到K”,事件B=“抽到黑桃”,则下列选项中正确的是
A.P(B|A)>(A)B.P(B|A)>P(B)C.P(B|A)+P(B|A)=1D.P(B|A)+P(B|A)=1
11.已知定义域为R的函数f(x)满足f(−x)=f(x)+2x,f(0)=2,且y=f(x+1)−1为奇函数,则
A.f(−1)=−3B.函数y=f(x)+x的一个周期为4
C.f(2024)=−2022D.∑19i=1f(i)=−150
三、填空题:本大题共3小题,每题5分,共15分.把答案填在题中的横线上.
12.(x2+2y)(x2−y)7的展开式中x4y6的系数为 .(用数字作答)
13.已知x>1,y>0,且x+2y=2,则1x−1+y的最小值是 .
14.阅读材料:“在成功概率为p的伯努利试验中,记首次出现连续两次成功时所需的试验次数的期望为E2,现提供一种求E2的方式:先进行第一次试验,若第一次试验失败,因为出现试验失败对出现连续两次成功毫无帮助,可以认为后续期望仍是E2,即总的试验次数为(E2+1);若第一次试验成功,则进行第二次试验,当第二次试验成功时,试验停止,此时试验次数为2,若第二次试验失败,相当于重新试验,此时总的试验次数为(E2+2).”请根据上述材料解决以下问题:设一个袋子里有红、黄、蓝色小球各一个现每次从袋子里取出一个球,确定颜色后放回,直到连续两次均取出红色球时为止,记此时取出球的次数为ξ,则ξ的数学期望为 .
四、解答题:本大题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.(13分)已知函数f(x)=(x2−ax−a)ex在(0,f(0))处的切线平行于直线2x+y+3=0.
(1)求a的值;
(2)求f(x)的极值.
16.(15分)河南省从2022年秋季启动新高考,新高考“3+1+2”模式中“3”为全国统一高考科目的语文、数学、外语,“1”为首选科目.要求从物理、历史2门科目中确定1门,“2”为再选科目,要求从思想政治、地理、化学、生物学4门科目中确定2门,共计产生12种组合.某班有学生50名,在选科时,首选科目选历史和物理的统计数据如下表所示:
附:χ2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d),其中n=a+b+c+d.
(1)根据表中的数据,判断是否有99.5%的把握认为学生选择历史与性别有关;
(2)从选择物理类的40名学生中按照分层抽样,任意抽取5名同学成立学习小组,该小组设正、副组长各一名,求正、副组长中至少有一名女同学的概率.
17.(15分)为迎接巴黎奥运会,甲、乙两名同学进行羽毛球练习,规定当有一人比对方多胜2局或打满6局时终止.甲在每局比赛中获胜的概率为p(p>0.5),前两局中甲和乙各胜一局的概率为49.
(1)求p的值;
(2)设终止时比赛局数为X,求X的分布列与期望.
18.(17分)2024年3月15日的“3·15”晚会后,为进一步加强市场计量监管,切实保护消费者合法权益,某市监管局对某夜市一条街内的电子计价秤进行检定,通过购买商品并比较商家称重和执法人员称重的结果偏差,超过误差范围则判定为缺斤少两.经检查,发现有10家商贩出现缺斤少两问题,执法人员已对这些商贩进行处罚,限期责令整改.以下是执法人员公布的10家“缺斤少两”商販的部分数据:商贩称重重量为xi、执法人员称重重量为yi,(单位:kg)∑10i=1xi=9.9,∑10i=1yi=7.1.其他数据如下:∑10i=1xi2=12.408,∑10i=1xiyi=9.146.
(1)利用最小二乘法,求执法人员称重重量y与商贩称重重量x之间的回归方程l1(a、b精确到0.001,下同);
(2)经核实,数据点(0.99,0.305)严重偏离回归方程,去除该点后利用相同方法重新计算回归方程l2,证明:l1与l2斜率相等,并求回归方程l2.
参考公式与数据:回归直线y=bx+a中斜率的最小二乘法估计公式为:b=∑ni=1(xi−x)(yi−y)∑ni=1(xi−x)2=∑ni=1xiyi−nxy∑ni=1xi2−nx2,a=y−bx,21172607≈0.812.
19.(17分)已知函数f(x)=ex−ax2−x,f′(x)为f(x)的导数.
(1)讨论f′(x)的单调性.
(2)若x=0是f(x)的极大值点,求a的取值范围.
(3)若θ∈(0,π2),证明:esinθ−1+ecsθ−1+ln(sinθcsθ)<1.
【参考答案】
安阳一中2023—2024学年第二学期期末考试
高二数学试题卷
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.B 2.D 3.B 4.B 5.C 6.A 7.C 8.D
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.BCD 10.AC 11.BC
三、填空题:本大题共3小题,每题5分,共15分.把答案填在题中的横线上.
12.−35
13.3+22
14.12
四、解答题:本大题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.(1) 解:由已知可得f′(x)=(2x−a)ex+(x2−ax−a)ex=(x2+2x−ax−2a)ex,
而直线2x+y+3=0的斜率为k=−2,所以f′(0)=−2a=−2⇒a=1;
(2) 由(1)得f(x)=(x2−x−1)⋅ex⇒f′(x)=ex⋅(x2+x−2)=ex⋅(x−1)(x+2),
当x∈(−∞,−2)时,f′(x)>0,函数f(x)单调递增;
当x∈(−2,1)时,f′(x)<0,函数f(x)单调递减;
当x∈(1,+∞)时,f′(x)>0,函数f(x)单调递增;
故极大值为f(−2)=5e2,极小值为f(1)=−e.
16.(1) 解:零假设为H0:学生选择历史与性别无关联
将表中的数据带入,得倒χ2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)=50×(216−16)225×25×10×40=8.
∴χ2>7.879=x0.005.根据小概率值α=0.005的独立性检验,我们推断H0不成立,即认为学生选择历史与性别有关,此推断犯错误的概率不大于0.005.
所以有99.5%的把握认为学生选择历史与性别有关.
(2) 法1:抽取的5名同学中,男生有3名,女生2名.设事件A为“选取2名同学担任正副组长中至少有一名女生”,则P(A)=1−C32C52=710(P(A)=1−A32A52=710).
法2:设事件M为“选取2名同学担任正副组长中至少有一名女生”,由题意知,抽取的5名同学中,男生有3名,设为A,B,C,女生2名,设为D,E,从这5名同学中选取2名同学担任正副组长,所有的可能情况有:
AB,AC,AD,AE,BC,BD,BE,CD,CE,DE,共计10种基本情况,且每种情况的发生是等可能的,其中至少有一名女生的情况有AD,AE,BD,BE,CD,CE,DE,共计有7种情况,所以P(M)=710.
17.(1) 解:由题意可得,甲在每局比赛中获胜的概率为p,则乙在每局比赛中获胜的概率为1−p,所以2p(1−p)=49,解得p=23或p=13,又p>0.5,所以p=23.
(2) 依题意X的所有可能值为2,4,6.
设每两局比赛为一轮,则该轮结束时比赛停止的概率(23)2+(13)2=59,
该轮结束时比赛继续的概率为1−59=49.
若该轮结束时比赛还将继续,则甲、乙在该轮中必是各胜一局,此时,该轮比赛结果对下轮比赛是否停止没有影响,从而有P(X=2)=59,P(X=4)=49×59=2081,
P(X=6)=(49)2=1681,故X的分布列如下:
所以E(X)=2×59+4×2081+6×1681=26681.
18.(1) 解:由题意x=110∑10i=1xi=0.99,y=110∑10i=1yi=0.71
故b=∑10i=1xiyi−xy∑10i=1xi2−10x2=9.146−10×0.99×−10×0.992=≈0.812,a=y−bx≈0.094
因此回归方程l1为y=0.812x−0.094
(2) 设被删除的数据点为(x10,y10),由题意x10=x,
设删除该数据点后,商贩称重重量和执法人员称重重量的平均值分别为x′、y′,
∴x′=19∑9i=1xi=19∑10i=1xi−x10=1910x−x=x=0.99,
y′=19∑9i=1yi=19(∑10i=1yi−y10)=19×(7.1−0.305)=0.755. 对于回归方程l2,b′=∑9i=1(xi−x′)(yi−y′)∑9i=1(xi−x′)2=∑10i=1(xi−x′)(yi−y′)−(x10−x′)(y10−y′)∑10i=1(xi−x′)2−(x10−x′)2
∵x10=x=x′,
∴b′=∑10i=1(xi−x′)(yi−y′)∑10i=1(xi−x′)2=∑10i=1xiyi−10xy′−10xy+10xy′∑10i=1xi2−10x2=∑10i=1xiyi−10xy∑10i=1xi2−10x2=b
∴斜率相等得证.∴a′=y′−b′x′≈−0.049
∴回归方程l2为y=0.812x−0.049
19.(1) 解:由题知f′(x)=ex−2ax−1,令g(x)=f′(x)=ex−2ax−1,
则g′(x)=ex−2a,
当a≤0时,g′(x)>0,f′(x)在区间(−∞,+∞)单调递增,
当a>0时,令g′(x)=0,解得x=ln2a,
当x∈(−∞,ln2a)时,g′(x)<0,
当x∈(ln2a,+∞)时,g′(x)>0,
所以f′(x)在区间(−∞,ln2a)上单调递减,在区间(ln2a,+∞)上单调递增,
综上所述,当a≤0时,f′(x)在区间(−∞,+∞)上单调递增;
当a>0时,f′(x)在区间(−∞,ln2a)上单调递减,在区间(ln2a,+∞)上单调递增.
(2) 当a≤0时,f′(0)=0,
由(1)知,当x∈(−∞,0)时,f′(x)<0,f(x)在(−∞,0)上单调递减;
当x∈(0,+∞)时,f′(x)>0,f(x)在(0,+∞)上单调递增;
所以x=0是函数f(x)的极小值点,不符合题意;
当0
当x∈(0,+∞)时,f′(x)>0,f(x)在(0,+∞)上单调递增;
所以x=0是函数f(x)的极小值点,不符合题意;
当a=12时,ln2a=0,则当x∈(−∞,+∞)时,f′(x)≥0,f(x)在(−∞,+∞)上单调递增,
所以f(x)无极值点,不合题意;当a>12时,ln2a>0,且f′(0)=0;
当x∈(−∞,0)时,f′(x)>0,f(x)在(−∞,0)上单调递增;
当x∈(0,ln2a)时,f′(x)<0,f(x)在(0,ln2a)上单调递减;
所以x=0是函数f(x)的极大值点,符合题意;
综上所述,a的取值范围是a>12.
(3) 要证esinθ−1+ecsθ−1+ln(sinθcsθ)<1,
只要证esinθ−1+ecsθ−1+ln(sinθ)+ln(csθ)
所以只要证对任意0
则ℎ(x)<ℎ(0)=0,即ln(1+x)
物理
合计
男生
1
24
25
女生
9
16
25
合计
10
40
50
a
0.100
0.050
0.010
0.005
0.001
xa
2.706
3.841
6.635
7.879
10.828
X
2
4
6
P
59
2081
1681
河南省安阳市第一中学2023-2024学年高二下学期第二次阶段考试(期中)数学试题: 这是一份河南省安阳市第一中学2023-2024学年高二下学期第二次阶段考试(期中)数学试题,共10页。
河南省安阳市林州市第一中学2023-2024学年高一下学期3月检测一数学试题: 这是一份河南省安阳市林州市第一中学2023-2024学年高一下学期3月检测一数学试题,共16页。试卷主要包含了函数的图象大致为,在中,给出下列四个式子,下列命题中正确的是等内容,欢迎下载使用。
河南省安阳市2023-2024学年高一上学期期末考试数学试题: 这是一份河南省安阳市2023-2024学年高一上学期期末考试数学试题,文件包含河南省安阳市2023-2024学年高一上学期期末考试数学试题docx、河南省安阳市20232024学年上高一年级期末数学命题报告pdf等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。












