





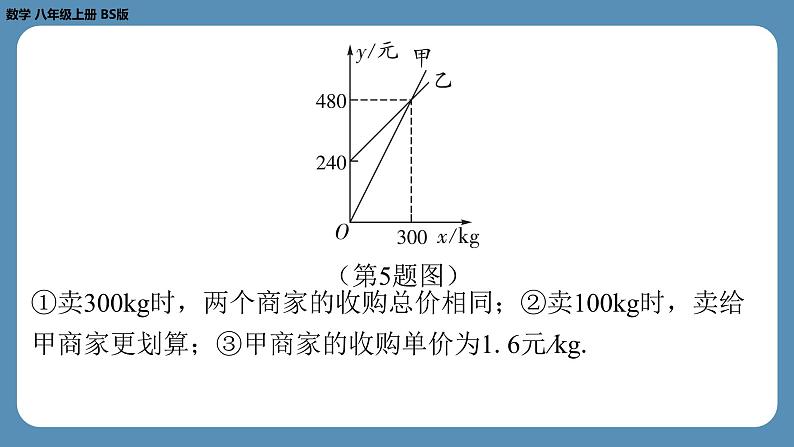
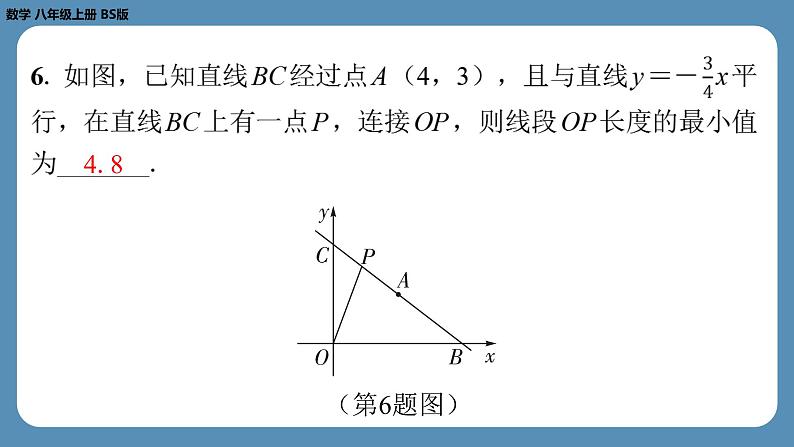
还剩22页未读,
继续阅读
2024-2025学年度北师版八上数学-专题5-一次函数中的综合问题【课外培优课件】
展开
这是一份2024-2025学年度北师版八上数学-专题5-一次函数中的综合问题【课外培优课件】,共30页。
第四章 一次函数专题5 一次函数中的综合问题 1. 在平面直角坐标系中,已知一次函数 y = mx + b ( m , b 均 为常数)与正比例函数 y = nx ( n 为常数)的图象如图所示,则 关于 x 的方程 mx = nx - b 的解为( A )A2. 在平面直角坐标系中,直线 y = kx +2与坐标轴交于 A , B 两 点,要使△ AOB 为等腰直角三角形,则这样的直线 y = kx +2有 ( B )B3. 甲、乙两车在某时段的速度随时间变化的图象如图所示.下 列结论错误的是( C )C4. 如图,已知 A (0,1), D (3,0),直线 l 绕点 A 旋转,与 x 轴交于点 P (点 P 不与点 D 重合).当△ OAP 与△ OAD 全等 时,点 P 的坐标为 .(-3,0) 5. 小明家准备卖一种农作物,现有甲、乙两个商家在收购,已 知两个商家的收购总价 y (元)与收购量 x (kg)的关系如图所 示(说明:乙商家先支付240元订金,若卖给乙商家,则不需退 回;否则,需退回订金),则以下说法正确的有 (填 序号).①③ ①卖300kg时,两个商家的收购总价相同;②卖100kg时,卖给 甲商家更划算;③甲商家的收购单价为1.6元/kg. 4.8 7. 如图,在平面直角坐标系中,点 A 的坐标为(2,7),点 B 的坐标为(0,5),在 x 轴上找一点 C ,使△ ABC 的周长最 小,求点 C 的坐标.解:如答图,作点 A 关于 x 轴的对称点A',连接A'B交 x 轴于点 C ,此时 CA + CB 的值最小.又因为 AB 的长为定值,所以此时 △ ABC 的周长最小.因为点 A 的坐标为(2,7),所以点A'的坐标为(2,-7).设直线A'B的函数表达式为 y = kx + b ( k ≠0).将A'(2,-7), B (0,5)代入 y = kx + b ,得2 k + b =-7, b =5.所以 k =-6.所以直线A'B的函数表达式为 y =-6 x +5. 答图8. 某游泳馆普通票价为20元/张,暑假为了促销,新推出两种优 惠卡.①金卡:600元/张,每次凭卡不再收费;②银卡:150元/张,每次凭卡另收10元.暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设 游泳 x 次时,所需总费用为 y 元.(1)分别写出选择银卡、普通票消费时, y 与 x 之间的函数关 系式;(2)在同一平面直角坐标系中,若三种消费方式对应的函数图 象如图所示,请求出点 A , B , C 的坐标;(3)请根据函数图象,直接写出选择哪种消费方式最划算.(2)当 x =0时,y =10 x +150=150,故点 A (0,150).当10 x +150=20 x 时,解得 x =15,则 y =300.故点 B (15,300).当 y =10 x +150=600时,解得 x =45.故点 C (45,600).解:(1)由题意,得银卡消费时, y =10 x +150;普通票消费时, y =20 x .(3)由点 A , B , C 的坐标,得当0< x <15时,选择普通票消费最划算;当 x =15时,选择银卡、普通票消费的总费用相同,均比选择金 卡划算;当15< x <45时,选择银卡消费最划算;当 x =45时,选择金卡、银卡消费的总费用相同,均比选择普通 票划算;当 x >45时,选择金卡消费最划算. 9. 若在直线 y =2 x +4上存在一点 P 到坐标轴的距离相等,则点 P 的坐标为 . 10. 在一条笔直的公路上有 A , B , C 三个休息站, C 休息站位 于 A , B 两个休息站之间.甲、乙两车分别从 A , B 两个休息站 出发,沿这条公路匀速行驶至 C 休息站停止.在甲车出发至甲车 到达 C 休息站的过程中,甲、乙两车各自与 C 地的距离 y (km)与甲车行驶时间 x (h)之间的函数关系如图所示.当甲 车出发 h时,两车相距350 km.1.5 【解析】由图可知, C 休息站到 A , B 休息站的距离均为 240km,甲的速度为240÷4=60(km/h),乙的速度为240÷ (4-1)=80(km/h).设甲出发 x h时,甲、乙两车相距350 km.由题意,得60 x +80( x -1)+350=240×2,解得 x = 1.5.故甲车出发1.5 h时,两车相距350 km.故答案为1.5. (1)直线 l2是否经过 x 轴上一定点?若经过,直接写出该定点 的坐标;若不经过,请说明理由.(2)过点 M (0,6)作平行于 x 轴的直线 l3,点 Q 为直线 l3上的 一个动点.当△ QAB 是不以点 A 为顶角顶点的等腰三角形时,求 点 Q 的坐标.解:(1)经过一定点.因为 y = kx +2 k ,所以 y = k ( x +2).所以当 x =-2时, y =0.所以直线 l2经过 x 轴上的定点(-2,0). 所以点 B 的坐标为(0,3). 所以点 A 的坐标为(6,0).如图,设点 Q 的坐标为( n ,6).①当 QB = QA 时,n2+(6-3)2=(6- n )2+(6-0)2, ②当 BQ = BA 时, n2+(6-3)2=(6-0)2+(3-0)2, 12. (选做)如图,点 A (8,6)在一个正比例函数的图象上, 点 B 的坐标为(16,0),连接 AB ,点 C 是线段 AB 的中点.点 P 在线段 OB 上以每秒2个单位长度的速度由点 O 向点 B 运动,点 Q 在射线 OA 上由点 O 向点 A 运动, P , Q 两点同时运动,同时 停止.设运动时间为 t s.(1)求该正比例函数的表达式.(2)连接 CP , PQ . 在点 P , Q 运动的过程中,△ OPQ 与△ BPC 能不能全等?如果能,求出点 Q 的运动速度;如果不能, 请说明理由. 若△ OPQ 与△ BPC 全等,则有以下两种情况: 演示完毕 谢谢观看
第四章 一次函数专题5 一次函数中的综合问题 1. 在平面直角坐标系中,已知一次函数 y = mx + b ( m , b 均 为常数)与正比例函数 y = nx ( n 为常数)的图象如图所示,则 关于 x 的方程 mx = nx - b 的解为( A )A2. 在平面直角坐标系中,直线 y = kx +2与坐标轴交于 A , B 两 点,要使△ AOB 为等腰直角三角形,则这样的直线 y = kx +2有 ( B )B3. 甲、乙两车在某时段的速度随时间变化的图象如图所示.下 列结论错误的是( C )C4. 如图,已知 A (0,1), D (3,0),直线 l 绕点 A 旋转,与 x 轴交于点 P (点 P 不与点 D 重合).当△ OAP 与△ OAD 全等 时,点 P 的坐标为 .(-3,0) 5. 小明家准备卖一种农作物,现有甲、乙两个商家在收购,已 知两个商家的收购总价 y (元)与收购量 x (kg)的关系如图所 示(说明:乙商家先支付240元订金,若卖给乙商家,则不需退 回;否则,需退回订金),则以下说法正确的有 (填 序号).①③ ①卖300kg时,两个商家的收购总价相同;②卖100kg时,卖给 甲商家更划算;③甲商家的收购单价为1.6元/kg. 4.8 7. 如图,在平面直角坐标系中,点 A 的坐标为(2,7),点 B 的坐标为(0,5),在 x 轴上找一点 C ,使△ ABC 的周长最 小,求点 C 的坐标.解:如答图,作点 A 关于 x 轴的对称点A',连接A'B交 x 轴于点 C ,此时 CA + CB 的值最小.又因为 AB 的长为定值,所以此时 △ ABC 的周长最小.因为点 A 的坐标为(2,7),所以点A'的坐标为(2,-7).设直线A'B的函数表达式为 y = kx + b ( k ≠0).将A'(2,-7), B (0,5)代入 y = kx + b ,得2 k + b =-7, b =5.所以 k =-6.所以直线A'B的函数表达式为 y =-6 x +5. 答图8. 某游泳馆普通票价为20元/张,暑假为了促销,新推出两种优 惠卡.①金卡:600元/张,每次凭卡不再收费;②银卡:150元/张,每次凭卡另收10元.暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设 游泳 x 次时,所需总费用为 y 元.(1)分别写出选择银卡、普通票消费时, y 与 x 之间的函数关 系式;(2)在同一平面直角坐标系中,若三种消费方式对应的函数图 象如图所示,请求出点 A , B , C 的坐标;(3)请根据函数图象,直接写出选择哪种消费方式最划算.(2)当 x =0时,y =10 x +150=150,故点 A (0,150).当10 x +150=20 x 时,解得 x =15,则 y =300.故点 B (15,300).当 y =10 x +150=600时,解得 x =45.故点 C (45,600).解:(1)由题意,得银卡消费时, y =10 x +150;普通票消费时, y =20 x .(3)由点 A , B , C 的坐标,得当0< x <15时,选择普通票消费最划算;当 x =15时,选择银卡、普通票消费的总费用相同,均比选择金 卡划算;当15< x <45时,选择银卡消费最划算;当 x =45时,选择金卡、银卡消费的总费用相同,均比选择普通 票划算;当 x >45时,选择金卡消费最划算. 9. 若在直线 y =2 x +4上存在一点 P 到坐标轴的距离相等,则点 P 的坐标为 . 10. 在一条笔直的公路上有 A , B , C 三个休息站, C 休息站位 于 A , B 两个休息站之间.甲、乙两车分别从 A , B 两个休息站 出发,沿这条公路匀速行驶至 C 休息站停止.在甲车出发至甲车 到达 C 休息站的过程中,甲、乙两车各自与 C 地的距离 y (km)与甲车行驶时间 x (h)之间的函数关系如图所示.当甲 车出发 h时,两车相距350 km.1.5 【解析】由图可知, C 休息站到 A , B 休息站的距离均为 240km,甲的速度为240÷4=60(km/h),乙的速度为240÷ (4-1)=80(km/h).设甲出发 x h时,甲、乙两车相距350 km.由题意,得60 x +80( x -1)+350=240×2,解得 x = 1.5.故甲车出发1.5 h时,两车相距350 km.故答案为1.5. (1)直线 l2是否经过 x 轴上一定点?若经过,直接写出该定点 的坐标;若不经过,请说明理由.(2)过点 M (0,6)作平行于 x 轴的直线 l3,点 Q 为直线 l3上的 一个动点.当△ QAB 是不以点 A 为顶角顶点的等腰三角形时,求 点 Q 的坐标.解:(1)经过一定点.因为 y = kx +2 k ,所以 y = k ( x +2).所以当 x =-2时, y =0.所以直线 l2经过 x 轴上的定点(-2,0). 所以点 B 的坐标为(0,3). 所以点 A 的坐标为(6,0).如图,设点 Q 的坐标为( n ,6).①当 QB = QA 时,n2+(6-3)2=(6- n )2+(6-0)2, ②当 BQ = BA 时, n2+(6-3)2=(6-0)2+(3-0)2, 12. (选做)如图,点 A (8,6)在一个正比例函数的图象上, 点 B 的坐标为(16,0),连接 AB ,点 C 是线段 AB 的中点.点 P 在线段 OB 上以每秒2个单位长度的速度由点 O 向点 B 运动,点 Q 在射线 OA 上由点 O 向点 A 运动, P , Q 两点同时运动,同时 停止.设运动时间为 t s.(1)求该正比例函数的表达式.(2)连接 CP , PQ . 在点 P , Q 运动的过程中,△ OPQ 与△ BPC 能不能全等?如果能,求出点 Q 的运动速度;如果不能, 请说明理由. 若△ OPQ 与△ BPC 全等,则有以下两种情况: 演示完毕 谢谢观看
相关资料
更多









