2025年高考数学一轮复习-4.2-导数与函数的单调性【课件】

这是一份2025年高考数学一轮复习-4.2-导数与函数的单调性【课件】，共49页。PPT课件主要包含了命题说明，必备知识·逐点夯实，单调递增，单调递减，常数函数，定义域，基础诊断·自测，1+∞，核心考点·分类突破，-3+∞等内容，欢迎下载使用。
【课标解读】【课程标准】1.结合实例,借助几何直观了解函数的单调性与导数的关系.2.能利用导数研究函数的单调性,会求函数的单调区间(其中多项式函数一般不超过三次).【核心素养】数学抽象、逻辑推理、数学运算.
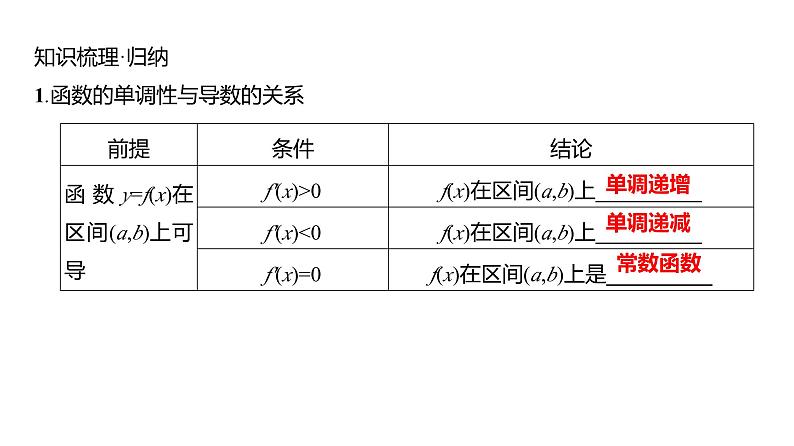
知识梳理·归纳1.函数的单调性与导数的关系
2.利用导数判断函数单调性的步骤第1步,确定函数的________;第2步,求出导数f'(x)的______;第3步,用f'(x)的零点将f(x)的定义域划分为若干个区间,列表给出f'(x)在各区间上的正负,由此得出函数y=f(x)在定义域内的单调性.
常用结论 1.若函数f(x)在(a,b)上单调递增,则x∈(a,b)时,f'(x)≥0恒成立;若函数f(x)在(a,b)上单调递减,则x∈(a,b)时,f'(x)≤0恒成立.2.若函数f(x)在(a,b)上存在单调递增区间,则x∈(a,b)时,f'(x)>0有解;若函数f(x)在(a,b)上存在单调递减区间,则x∈(a,b)时,f'(x)0在[1,2]上有解,即a>-2x2-x在[1,2]上有解,所以a>(-2x2-x)min,又(-2x2-x)min=-10,所以a>-10,所以实数a的取值范围是(-10,+∞).
(2)(2023·全国乙卷)设a∈(0,1),若函数f(x)=ax+(1+a)x在(0,+∞)上单调递增,则a的取值范围是______________. 
解题技法1.利用导数比较大小,其关键是判断已知(或构造后的)函数的单调性,利用其单调性比较大小.2.与函数有关的不等式,要充分挖掘条件关系,恰当构造函数,再利用导数研究新函数的单调性,从而解不等式.
3.根据函数单调性求参数的方法:(1)利用集合间的包含关系处理:y=f(x)在(a,b)上单调,则区间(a,b)是相应单调区间的子集.(2)f(x)为增(减)函数的充要条件是对任意的x∈(a,b)都有f'(x)≥0(f'(x)≤0),且在(a,b)内的任一非空子区间上,f'(x)不恒为零,应注意此时式子中的等号不能省略,否则会漏解.(3)若函数y=f(x)在区间(a,b)上不单调,则转化为f'(x)=0在(a,b)上有解(需验证解的两侧导数是否异号).
2.已知定义域为R的函数f(x)的导数为f'(x),且满足f'(x)x2-1的解集是(　　)A.(-∞,-1)B.(-1,+∞)C.(2,+∞)D.(-∞,2)
【解析】选D.令g(x)=f(x)-x2,则g'(x)=f'(x)-2xx2-1可化为f(x)-x2>-1,而g(2)=f(2)-22=3-4=-1,所以该不等式可化为g(x)>g(2),故该不等式的解集为(-∞,2).