2025年高考数学一轮复习-6.5.2-余弦定理、正弦定理应用举例【课件】

这是一份2025年高考数学一轮复习-6.5.2-余弦定理、正弦定理应用举例【课件】，共40页。PPT课件主要包含了命题说明，必备知识·逐点夯实，指北方向顺时针旋转α，指北方向逆时针旋转α，坡面与水平面，水平长度，核心考点·分类突破等内容，欢迎下载使用。
【课标解读】【课程标准】能用余弦定理、正弦定理解决简单的实际问题.【核心素养】数学抽象、数学运算、逻辑推理.
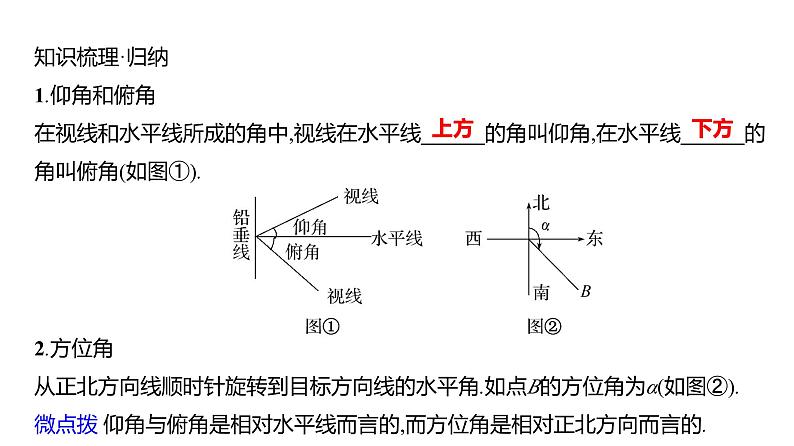
知识梳理·归纳1.仰角和俯角在视线和水平线所成的角中,视线在水平线______的角叫仰角,在水平线______的角叫俯角(如图①).2.方位角从正北方向线顺时针旋转到目标方向线的水平角.如点B的方位角为α(如图②).微点拨 仰角与俯角是相对水平线而言的,而方位角是相对正北方向而言的.
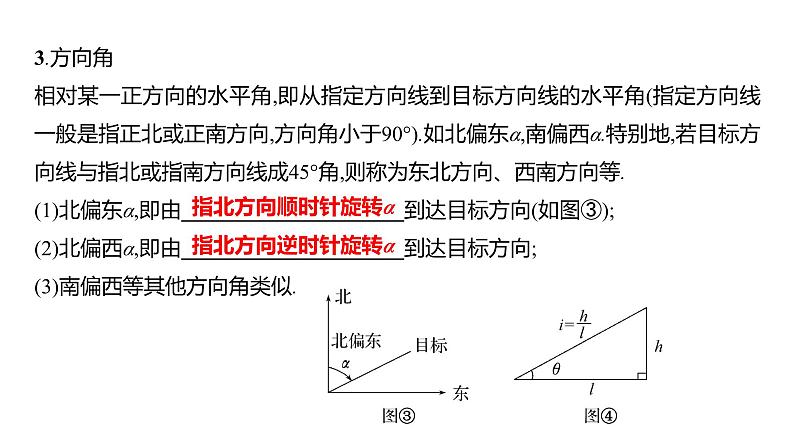
3.方向角相对某一正方向的水平角,即从指定方向线到目标方向线的水平角(指定方向线一般是指正北或正南方向,方向角小于90°).如北偏东α,南偏西α.特别地,若目标方向线与指北或指南方向线成45°角,则称为东北方向、西南方向等.(1)北偏东α,即由_____________________到达目标方向(如图③);(2)北偏西α,即由_____________________到达目标方向;(3)南偏西等其他方向角类似.
4.坡角与坡度(1)坡角:______________所成的二面角(如图④,角θ为坡角).(2)坡度:坡面的铅直高度与__________之比(如图④,i为坡度),坡度又称为坡比.
2.(弄错方向角的含义)如图所示,两座灯塔A和B与海岸观察站C的距离相等,灯塔A在观察站的南偏西40°方向上,灯塔B在观察站的南偏东60°方向上,则灯塔A在灯塔B的(　　)A. 北偏东10°方向上B. 北偏西10°方向上C. 南偏东80°方向上D. 南偏西80°方向上【解析】选D. 由条件及题图可知,△ABC为等腰三角形,所以∠BAC=∠ABC=40°,又∠BCD=60°,所以∠CBD=30°,所以∠DBA=10°,因此灯塔A在灯塔B的南偏西80°方向上.
解题技法距离问题的类型及解法(1)类型:①两点间既不可达也不可视,②两点间可视但不可达,③两点都不可达.(2)解法:选择合适的辅助测量点,构造三角形,将问题转化为求某个三角形的边长问题,从而利用正、余弦定理求解.
对点训练1.(2023·青岛模拟)海洋蓝洞是地球罕见的自然地理现象,被喻为“地球给人类保留宇宙秘密的最后遗产”,若要测量如图所示某蓝洞洞口边缘A,B两点间的距离,现在珊瑚群岛上取两点C,D,测得CD=8海里,∠ADB=135°,∠BDC=∠DCA=15°,∠ACB=120°,则A,B两点的距离为　　　　　海里. 
考点二测量高度问题[例2](1)如图,某同学为测量鹳雀楼的高度MN,在鹳雀楼的正东方向找到一座建筑物AB,高约为37 m,在地面上点C处(B,C,N三点共线)测得建筑物顶部A,鹳雀楼顶部M的仰角分别为30°和45°,在A处测得鹳雀楼顶部M的仰角为15°,则鹳雀楼的高度约为(　　)A. 91 m　B. 74 m　C. 64 m　D. 52 m
解题技法测量高度问题的求解策略(1)理解仰角、俯角、方向(位)角是关键.(2)在实际问题中,若遇到空间与平面(地面)同时研究的问题,最好画两个图形,一个空间图形,一个平面图形.(3)注意山或塔垂直于地面或海平面,把空间问题转化为平面问题.
2.(2023·江门模拟)某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:A,B,C三地位于同一水平面上,在C处进行该仪器的垂直弹射,观测点A,B两地相距100米,∠BAC=60°,BC的距离比AC短40米.A地测得该仪器弹至最高点H时的仰角为30°.(1)求A,C两地间的距离;【解析】(1)由题意,设AC=x,则BC=x-40.在△ABC中,由余弦定理,得BC2=BA2+AC2-2BA·ACcs∠BAC,即(x-40)2=10 000+x2-100x,解得x=420,所以A,C两地间的距离为420米.
解题技法测量角度问题的求解策略测量角度问题的关键是在弄清题意的基础上,画出表示实际问题的图形,并在图形中标出有关的角和距离,再用正弦定理或余弦定理解三角形,最后将解得的结果转化为实际问题的解.提醒:确定方向角时,必须先弄清楚是哪一个点的方向角.
对点训练(2023·赣州模拟)如图,某运动员从A市出发沿海岸一条笔直的公路以每小时15km的速度向东进行长跑训练,长跑开始时,在A市南偏东方向距A市75 km的B处有一艘小艇,小艇与海岸距离为45 km,若小艇与该运动员同时出发,要追上这位运动员.(1)小艇至少以多大的速度行驶才能追上这位运动员?