




还剩45页未读,
继续阅读
所属成套资源:全套苏科版初中八年级数学上册素养综合检测课件
成套系列资料,整套一键下载
苏科版初中八年级数学上册第6章素养综合检测课件
展开
这是一份苏科版初中八年级数学上册第6章素养综合检测课件,共53页。
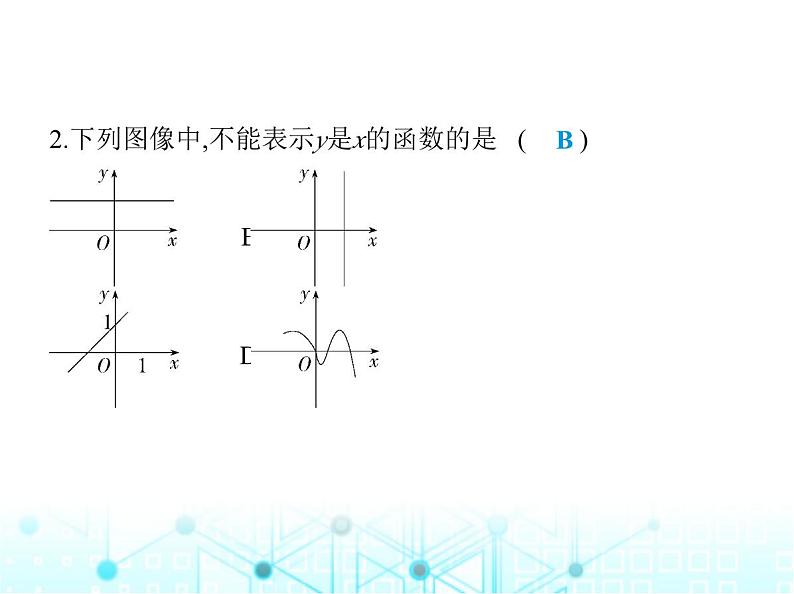
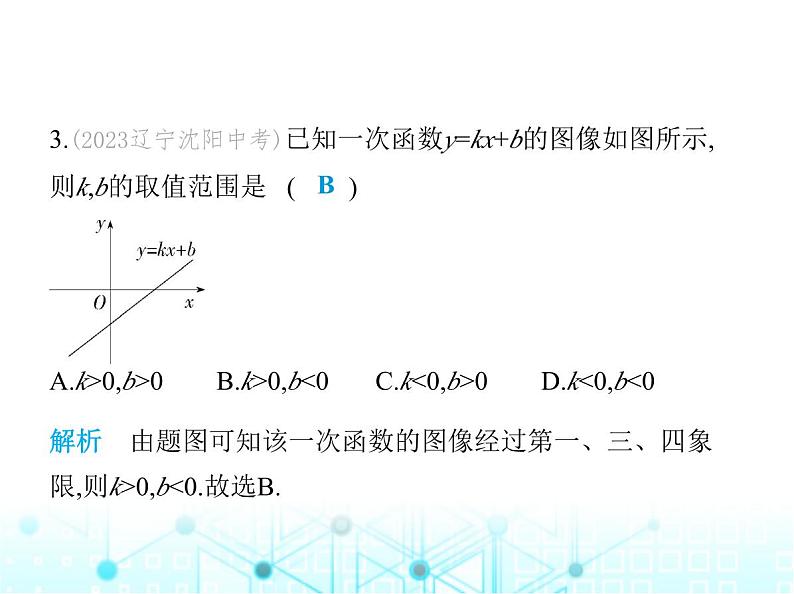
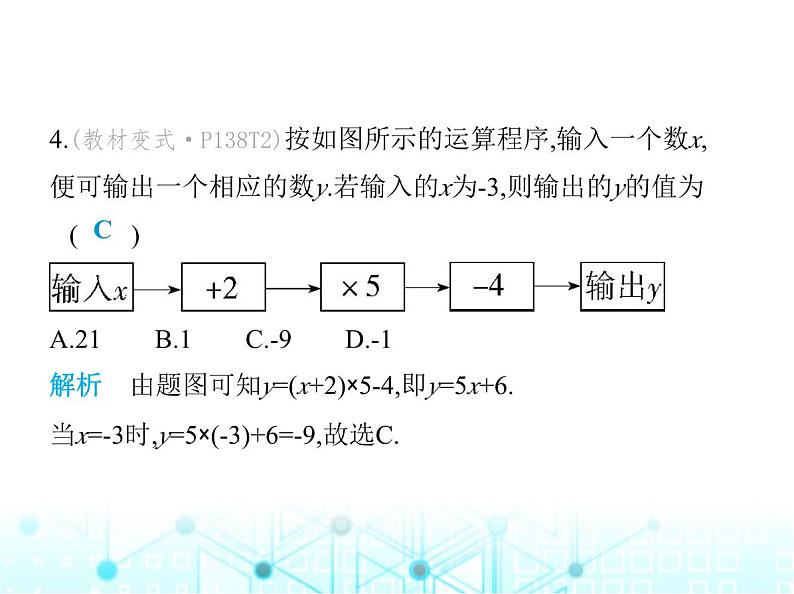
一、选择题(每题3分,共8小题,共24分)1.(新独家原创)盐泰锡常宜城际铁路是一条连接盐城市、无 锡市和宜兴市的高速铁路,全线在江苏省内,贯通苏北、苏 中、苏南,设计时速350 km.若一列高铁以每小时320 km的速 度行驶,则它行驶的路程s(km)与时间t(h)之间的关系可用公 式s=320t来表示,下列说法正确的是 ( )CA.320和s,t都是变量B.s是常量,320和t是变量C.320是常量,s和t是变量D.t是常量,320和s是变量解析 由题意得320是常量,行驶过程中时间不断增加,t的值 不断变化,是变量,路程随时间t的变化而变化,s也是变量, ∴A,B,D均不合题意,C符合题意.故选C.2.下列图像中,不能表示y是x的函数的是 ( ) A B C DB解析 A,C,D中的图像,对于自变量x的每一个值,因变量y都 有唯一的值与它对应,所以y是x的函数,故A,C,D不符合题意; B.一个x对应所有的实数y,所以y不是x的函数,故B符合题意. 故选B.3.(2023辽宁沈阳中考)已知一次函数y=kx+b的图像如图所示, 则k,b的取值范围是 ( ) A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0解析 由题图可知该一次函数的图像经过第一、三、四象 限,则k>0,b<0.故选B.B4.(教材变式·P138T2)按如图所示的运算程序,输入一个数x, 便可输出一个相应的数y.若输入的x为-3,则输出的y的值为 ( ) A.21 B.1 C.-9 D.-1C解析 由题图可知y=(x+2)×5-4,即y=5x+6.当x=-3时,y=5×(-3)+6=-9,故选C.5.下列关于一次函数y=-2x+2的说法中,错误的是 ( )A.图像经过第一、二、四象限B.图像与x轴的交点坐标为(1,0)C.当x>0时,y>2D.y的值随着x的值的增大而减小C解析 该函数图像经过第一、二、四象限,故选项A正确,不 符合题意;当y=0时,x=1,故选项B正确,不符合题意;当x=0时,y=2,故当x>0时,y<2,故选项C错误,符合题意;∵k=-2<0,∴y的值随着x的值的增大而减小,故选项D正确,不 符合题意.故选C.6.如图,已知一次函数y=kx+b的图像与x轴,y轴分别交于点(2, 0),点(0,3).下列结论:①图像经过点(1,-3);②关于x的方程kx+b =0的解为x=2;③关于x的方程kx+b=3的解为x=0;④当x>2时,y <0.其中正确的是 ( )A.①②③ B.①③④ C.②③④ D.①②④C解析 把点(2,0),点(0,3)代入y=kx+b,得 解得 ∴一次函数的解析式为y=- x+3,当x=1时,y= ,∴图像不经过点(1,-3),故①不符合题意;由图像得,关于x的方程kx +b=0的解为x=2,故②符合题意;关于x的方程kx+b=3的解为x= 0,故③符合题意;当x>2时,y<0,故④符合题意.故选C.7.(2023四川雅安中考)在平面直角坐标系中,将函数y=x的图 像绕坐标原点逆时针旋转90°,再向上平移1个单位长度,所得 直线的函数表达式为 ( )A.y=-x+1 B.y=x+1 C.y=-x-1 D.y=x-1A解析 在函数y=x的图像上取点A(1,1),绕原点逆时针旋转90 °后得到对应的点的坐标为A'(-1,1),则旋转后的直线的解析 式为y=-x,再向上平移1个单位长度,得到直线y=-x+1.故选A.8.(新考向·规律探究试题)如图,直线y=x+2与y轴相交于点A0, 过点A0作x轴的平行线交直线y=0.5x+1于点B1,过点B1作y轴的 平行线交直线y=x+2于点A1,过点A1作x轴的平行线交直线y= 0.5x+1于点B2,过点B2作y轴的平行线交直线y=x+2于点A2,… …,依此类推,得到直线y=x+2上的点A1,A2,A3,…,与直线y=0.5x +1上的点B1,B2,B3,…,则A7B8的长为 ( )C A.64 B.128 C.256 D.512解析 对于直线y=x+2,当x=0时,y=2,即A0(0,2),∵A0B1∥x轴, ∴B1的纵坐标为2,将y=2代入y=0.5x+1,得x=2,即B1(2,2),∴A0B1 =2=21,∵A1B1∥y轴,∴A1的横坐标为2,将x=2代入y=x+2,得y= 4,即A1(2,4),∴B2的纵坐标为4,将y=4代入y=0.5x+1,得x=6,即B2 (6,4),∴A1B2=4=22,同理A2B3=8=23,……,An-1Bn=2n,则A7B8的长为 28=256.故选C.9.在函数y= 中,自变量x的取值范围是 . x<1解析 根据被开方数大于等于0,分母不等于0,得1-x>0,解得x <1.二、填空题(每题3分,共10小题,共30分)10.(跨学科·地理)“二十四节气”是华夏祖先历经千百年的 实践创造出来的宝贵科学遗产,它与白昼时长密切相关,是反 映天气气候和物候变化、掌握农事季节的工具.如图所示的 是某地区一年中部分节气所对应的白昼时长示意图,则立 春、清明、寒露、小寒这四个节气中,白昼时长最短的节气 是 .小寒解析 由图像可知,在立春、清明、寒露、小寒这四个节气 中,白昼时长最短的节气是小寒.故答案为小寒.11.若方程组 的解是 则直线y=-2x+b与直线y=x-a的交点坐标是 .(-1,3)12.直线y=kx+b如图所示,则代数式2k-b的值为 .-3解析 ∵y=kx+b的图像经过点(-2,3),∴3=-2k+b,∴2k-b=-3,故答案为-3.13.(新独家原创)已知y关于x的函数y=(m+2)x+m2-4是正比例 函数,则(2m-5)2 024的值是 .1解析 根据题意得m+2≠0且m2-4=0,解得m=2.则(2m-5)2 024=(2 ×2-5)2 024=1.14.若一次函数y=kx+3在-2≤x≤4的范围内有最大值,为19,则 k= .-8或4解析 ①当x=-2时,y取得最大值,为19,则-2k+3=19,解得k=-8; ②当x=4时,y取得最大值,为19,则4k+3=19,解得k=4.∴k的值 为-8或4,故答案为-8或4.15.1~6个月的婴儿生长发育非常快,他们的体重y(克)与月龄x (月)之间的关系可以用y=a+800x来近似地表示,其中a是婴儿 出生时的体重.某个婴儿出生时的体重是3 800克,月龄x= 时体重是7 000克.4解析 将a=3 800,y=7 000代入y=a+800x,得7 000=3 800+800x,解得x=4.故答案为4.16.(新考向·新定义试题)我们把函数图像上横坐标与纵坐标 互为相反数的点定义为这个函数图像上的“友善点”.例如 在正比例函数y=-x的图像上,存在一点P(-1,1),则点P为正比 例函数y=-x图像上的“友善点”,则一次函数y=-5x-2图像上 的“友善点”是 . 解析 设一次函数y=-5x-2图像上的“友善点”为(x,-5x-2), 则-5x-2+x=0,解得x=- ,∴-5x-2=-5× -2= .∴一次函数y=-5x-2图像上的“友善点”为 .17.(情境题·国家安全)如图,在一次实战化军演中,某空军加 油飞机接到命令,立即给另一架正在飞行的运输机进行空中 加油.在加油过程中,设运输飞机的油箱余油量为Q1吨,加油 飞机的加油箱余油量为Q2吨,加油时间为t(分),Q1、Q2与t之 间的函数图像如图所示,结合图像判断,下列说法正确的是 .(把正确的序号都填写上)①③ ①加油之前,加油飞机的加油油箱中有30吨油;②加油之前,运输飞机的油箱余油量为69-40=29吨;③加油飞机的加油箱的油全部加给运输飞机需10分钟;④运输飞机加完油后,以原速继续飞行,如果每分钟油耗相 同,最多能飞行12小时.解析 由题意及题图得加油之前,加油飞机的加油油箱中有 30吨油,故①说法正确;加油之前,运输飞机的油箱余油量为4 0吨,故②说法错误;加油飞机的加油箱的油全部加给运输飞 机需10分钟,故③说法正确;∵运输飞机在10分钟内,加油29 吨,加油飞机的加油箱的油减少了30吨,∴10分钟内运输飞机 耗油量为1吨,∴运输飞机每分钟耗油量为0.1吨,∴运输飞机 每小时耗油量为6吨,∵69÷6=11.5(小时),∴运输飞机加完油 后,以原速继续飞行,如果每分钟油耗相同,最多能飞行11.5小 时,故④说法错误.∴说法正确的是①③.故答案为①③.18.如图,已知A(2,3),B(0,2),在x轴上找一点C,使得|AC-BC|的 值最大,则此时点C的坐标为 .(-4,0)解析 如图所示,连接AB并延长交x轴于点C, 此时|AC-BC|的值最大,为AB的长,点C为所求的点.设直线AB 的解析式为y=kx+b(k≠0),把A(2,3),B(0,2)代入,得 解得 故直线AB的解析式为y= x+2.令y= x+2=0,则x=-4,故点C的坐标为(-4,0).故答案为(-4,0).19.(6分)若y-2与2x+3成正比例,且当x=1时,y=12.(1)求y与x的函数解析式.(2)求当y=4时,x的值.三、解答题(共6小题,共46分)解析 (1)设y-2=k(2x+3),把x=1,y=12代入,得12-2=5k,解得k=2,所以y-2=2(2x+3),所以y与x之间的函数关系式为y=4x+8.(2)当y=4时,4x+8=4,解得x=-1.20.(跨学科·物理)(7分)世界上大部分国家都使用摄氏温度, 少数国家使用华氏温度.两种计量之间有如下对应.(1)如果两种计量之间的关系是一次函数关系,设摄氏温度为 x(℃)时对应的华氏温度为y(°F),请你写出华氏温度关于摄氏 温度的函数表达式.(2)当华氏温度为0°F时,摄氏温度是多少℃?(3)华氏温度的值与对应的摄氏温度的值有可能相等吗?若可 能,求出此值;若不可能,请说明理由.解析 (1)设华氏温度y(°F)与摄氏温度x(℃)之间的函数关系 式为y=kx+b(k≠0),把(0,32),(10,50)代入,得 解得 ∴华氏温度y(°F)与摄氏温度x(℃)之间的函数关系式为y=1.8 x+32.(2)当y=0时,0=1.8x+32,解得x=- ,故当华氏温度为0°F时,摄氏温度是- ℃.(3)华氏温度的值与对应的摄氏温度的值有可能相等.当y=x 时,x=1.8x+32,解得x=-40.∴当华氏温度为-40 °F时,摄氏温度是-40 ℃.21.(7分)画出一次函数y=-2x+3的图像,根据图像解决下列问 题.(1)写出直线上横坐标是2的点的坐标.(2)写出y>0时,x的取值范围.(3)写出直线上到x轴的距离等于4的点的坐标.解析 直线y=-2x+3过点(0,3)、(1.5,0),如图. (1)如图,直线上横坐标是2的点的坐标是(2,-1).(2)由图像可得y>0时,x的取值范围是x<1.5.(3)当y=4时,4=-2x+3,解得x=-0.5,当y=-4时,-4=-2x+3,解得x=3.5,即直线上到x轴的距离等于4的点的坐标是(-0.5,4)或(3.5,-4).22.(教材变式·P138T1)(8分)【问题情境】“漏壶”是一种古 代计时器,在社会实践活动中,某小组同学根据“漏壶”的原 理制作了如图①所示的液体漏壶,漏壶可看成是由一个圆锥 和一个圆柱组成的,中间连通,液体可以从圆锥容器中匀速漏 到圆柱容器中,实验开始时圆柱容器中已有一部分液体.【实验观察】(1)下表是实验记录的圆柱体容器液面高度y (厘米)与时间x(小时)的数据:请你利用数据画出图像.【探索发现】(2)请你根据表中的数据及图像,用所学过的函 数的知识确定y与x之间的函数解析式.【结论应用】(3)如果本次实验记录的开始时间是上午9:00, 那么当圆柱容器中液面高度达到12厘米时是几点?解析 (1)描出各点,并连接,如图. (2)由(1)中的图像可知该函数为一次函数,设该函数的表达式 为y=kx+b(k≠0),∵点(1,6),(2,10)在该函数图像上,∴ 解得 ∴y与x的函数表达式为y=4x+2.(3)当y=12时,即4x+2=12,解得x=2.5,9+2.5=11.5,即圆柱容器中 液面高度达到12厘米时是上午11:30.23.(2023四川成都中考)(8分)2023年7月28日至8月8日,第31 届世界大学生运动会在成都举行.“当好东道主,热情迎嘉 宾”,成都某知名小吃店计划购买A,B两种食材制作小吃.已 知购买1千克A种食材和1千克B种食材共需68元,购买5千克A 种食材和3千克B种食材共需280元.(1)求A,B两种食材的价格.(2)该小吃店计划购买两种食材共36千克,其中购买A种食材 千克数不少于B种食材千克数的2倍,当A,B两种食材分别购 买多少千克时,总费用最少?并求出最少总费用.解析 (1)设A种食材的价格为x元/千克,B种食材的价格为y 元/千克.根据题意,得 解得 答:A种食材的价格是每千克38元,B种食材的价格是每千克30元.(2)设A种食材购买m千克,总费用为w元,则B种食材购买(36 -m)千克.根据题意,得w=38m+30(36-m)=8m+1 080.∵m≥2(36-m),∴24≤m<36.∵k=8>0,∴w随m的增大而增大,∴当m=24时,w有最小值,为8×24+1 080=1 272(元),∴A种食材购买24千克,B种食材购买12千克时,总费用最少, 为1 272元.24.(新考向·过程性学习试题)(10分)【直观想象】如图1,动点P在数轴上从负半轴向正半轴运动, 点P到原点的距离先变小再变大,当点P的位置确定时,点P到 原点的距离也确定.【数学发现】当一个动点P(x,0)到一个定点的距离为d时,我 们发现d是x的函数.【数学理解】(1)动点P(x,0)到定点A(2,0)的距离为d,当x= 时,d取最小值.【类比迁移】(2)设动点P(x,0)到两个定点M(1,0)、N(3,0)的距离和为y.①随着x增大,y怎样变化?②在图2的平面直角坐标系中画出y关于x的函数图像.③当y>6时,x的取值范围是 . 图1 图2解析 (1)当A,P重合时,d最小,为0,此时x=2.故答案为2.(2)①当x<1时,随着x增大,y变小;当1≤x≤3时,随着x增大,y不 变;当x>3时,随着x增大,y变大.②如图.③观察图像可知,满足条件的x的取值范围为x<-1或x>5.故答 案为x<-1或x>5.
一、选择题(每题3分,共8小题,共24分)1.(新独家原创)盐泰锡常宜城际铁路是一条连接盐城市、无 锡市和宜兴市的高速铁路,全线在江苏省内,贯通苏北、苏 中、苏南,设计时速350 km.若一列高铁以每小时320 km的速 度行驶,则它行驶的路程s(km)与时间t(h)之间的关系可用公 式s=320t来表示,下列说法正确的是 ( )CA.320和s,t都是变量B.s是常量,320和t是变量C.320是常量,s和t是变量D.t是常量,320和s是变量解析 由题意得320是常量,行驶过程中时间不断增加,t的值 不断变化,是变量,路程随时间t的变化而变化,s也是变量, ∴A,B,D均不合题意,C符合题意.故选C.2.下列图像中,不能表示y是x的函数的是 ( ) A B C DB解析 A,C,D中的图像,对于自变量x的每一个值,因变量y都 有唯一的值与它对应,所以y是x的函数,故A,C,D不符合题意; B.一个x对应所有的实数y,所以y不是x的函数,故B符合题意. 故选B.3.(2023辽宁沈阳中考)已知一次函数y=kx+b的图像如图所示, 则k,b的取值范围是 ( ) A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0解析 由题图可知该一次函数的图像经过第一、三、四象 限,则k>0,b<0.故选B.B4.(教材变式·P138T2)按如图所示的运算程序,输入一个数x, 便可输出一个相应的数y.若输入的x为-3,则输出的y的值为 ( ) A.21 B.1 C.-9 D.-1C解析 由题图可知y=(x+2)×5-4,即y=5x+6.当x=-3时,y=5×(-3)+6=-9,故选C.5.下列关于一次函数y=-2x+2的说法中,错误的是 ( )A.图像经过第一、二、四象限B.图像与x轴的交点坐标为(1,0)C.当x>0时,y>2D.y的值随着x的值的增大而减小C解析 该函数图像经过第一、二、四象限,故选项A正确,不 符合题意;当y=0时,x=1,故选项B正确,不符合题意;当x=0时,y=2,故当x>0时,y<2,故选项C错误,符合题意;∵k=-2<0,∴y的值随着x的值的增大而减小,故选项D正确,不 符合题意.故选C.6.如图,已知一次函数y=kx+b的图像与x轴,y轴分别交于点(2, 0),点(0,3).下列结论:①图像经过点(1,-3);②关于x的方程kx+b =0的解为x=2;③关于x的方程kx+b=3的解为x=0;④当x>2时,y <0.其中正确的是 ( )A.①②③ B.①③④ C.②③④ D.①②④C解析 把点(2,0),点(0,3)代入y=kx+b,得 解得 ∴一次函数的解析式为y=- x+3,当x=1时,y= ,∴图像不经过点(1,-3),故①不符合题意;由图像得,关于x的方程kx +b=0的解为x=2,故②符合题意;关于x的方程kx+b=3的解为x= 0,故③符合题意;当x>2时,y<0,故④符合题意.故选C.7.(2023四川雅安中考)在平面直角坐标系中,将函数y=x的图 像绕坐标原点逆时针旋转90°,再向上平移1个单位长度,所得 直线的函数表达式为 ( )A.y=-x+1 B.y=x+1 C.y=-x-1 D.y=x-1A解析 在函数y=x的图像上取点A(1,1),绕原点逆时针旋转90 °后得到对应的点的坐标为A'(-1,1),则旋转后的直线的解析 式为y=-x,再向上平移1个单位长度,得到直线y=-x+1.故选A.8.(新考向·规律探究试题)如图,直线y=x+2与y轴相交于点A0, 过点A0作x轴的平行线交直线y=0.5x+1于点B1,过点B1作y轴的 平行线交直线y=x+2于点A1,过点A1作x轴的平行线交直线y= 0.5x+1于点B2,过点B2作y轴的平行线交直线y=x+2于点A2,… …,依此类推,得到直线y=x+2上的点A1,A2,A3,…,与直线y=0.5x +1上的点B1,B2,B3,…,则A7B8的长为 ( )C A.64 B.128 C.256 D.512解析 对于直线y=x+2,当x=0时,y=2,即A0(0,2),∵A0B1∥x轴, ∴B1的纵坐标为2,将y=2代入y=0.5x+1,得x=2,即B1(2,2),∴A0B1 =2=21,∵A1B1∥y轴,∴A1的横坐标为2,将x=2代入y=x+2,得y= 4,即A1(2,4),∴B2的纵坐标为4,将y=4代入y=0.5x+1,得x=6,即B2 (6,4),∴A1B2=4=22,同理A2B3=8=23,……,An-1Bn=2n,则A7B8的长为 28=256.故选C.9.在函数y= 中,自变量x的取值范围是 . x<1解析 根据被开方数大于等于0,分母不等于0,得1-x>0,解得x <1.二、填空题(每题3分,共10小题,共30分)10.(跨学科·地理)“二十四节气”是华夏祖先历经千百年的 实践创造出来的宝贵科学遗产,它与白昼时长密切相关,是反 映天气气候和物候变化、掌握农事季节的工具.如图所示的 是某地区一年中部分节气所对应的白昼时长示意图,则立 春、清明、寒露、小寒这四个节气中,白昼时长最短的节气 是 .小寒解析 由图像可知,在立春、清明、寒露、小寒这四个节气 中,白昼时长最短的节气是小寒.故答案为小寒.11.若方程组 的解是 则直线y=-2x+b与直线y=x-a的交点坐标是 .(-1,3)12.直线y=kx+b如图所示,则代数式2k-b的值为 .-3解析 ∵y=kx+b的图像经过点(-2,3),∴3=-2k+b,∴2k-b=-3,故答案为-3.13.(新独家原创)已知y关于x的函数y=(m+2)x+m2-4是正比例 函数,则(2m-5)2 024的值是 .1解析 根据题意得m+2≠0且m2-4=0,解得m=2.则(2m-5)2 024=(2 ×2-5)2 024=1.14.若一次函数y=kx+3在-2≤x≤4的范围内有最大值,为19,则 k= .-8或4解析 ①当x=-2时,y取得最大值,为19,则-2k+3=19,解得k=-8; ②当x=4时,y取得最大值,为19,则4k+3=19,解得k=4.∴k的值 为-8或4,故答案为-8或4.15.1~6个月的婴儿生长发育非常快,他们的体重y(克)与月龄x (月)之间的关系可以用y=a+800x来近似地表示,其中a是婴儿 出生时的体重.某个婴儿出生时的体重是3 800克,月龄x= 时体重是7 000克.4解析 将a=3 800,y=7 000代入y=a+800x,得7 000=3 800+800x,解得x=4.故答案为4.16.(新考向·新定义试题)我们把函数图像上横坐标与纵坐标 互为相反数的点定义为这个函数图像上的“友善点”.例如 在正比例函数y=-x的图像上,存在一点P(-1,1),则点P为正比 例函数y=-x图像上的“友善点”,则一次函数y=-5x-2图像上 的“友善点”是 . 解析 设一次函数y=-5x-2图像上的“友善点”为(x,-5x-2), 则-5x-2+x=0,解得x=- ,∴-5x-2=-5× -2= .∴一次函数y=-5x-2图像上的“友善点”为 .17.(情境题·国家安全)如图,在一次实战化军演中,某空军加 油飞机接到命令,立即给另一架正在飞行的运输机进行空中 加油.在加油过程中,设运输飞机的油箱余油量为Q1吨,加油 飞机的加油箱余油量为Q2吨,加油时间为t(分),Q1、Q2与t之 间的函数图像如图所示,结合图像判断,下列说法正确的是 .(把正确的序号都填写上)①③ ①加油之前,加油飞机的加油油箱中有30吨油;②加油之前,运输飞机的油箱余油量为69-40=29吨;③加油飞机的加油箱的油全部加给运输飞机需10分钟;④运输飞机加完油后,以原速继续飞行,如果每分钟油耗相 同,最多能飞行12小时.解析 由题意及题图得加油之前,加油飞机的加油油箱中有 30吨油,故①说法正确;加油之前,运输飞机的油箱余油量为4 0吨,故②说法错误;加油飞机的加油箱的油全部加给运输飞 机需10分钟,故③说法正确;∵运输飞机在10分钟内,加油29 吨,加油飞机的加油箱的油减少了30吨,∴10分钟内运输飞机 耗油量为1吨,∴运输飞机每分钟耗油量为0.1吨,∴运输飞机 每小时耗油量为6吨,∵69÷6=11.5(小时),∴运输飞机加完油 后,以原速继续飞行,如果每分钟油耗相同,最多能飞行11.5小 时,故④说法错误.∴说法正确的是①③.故答案为①③.18.如图,已知A(2,3),B(0,2),在x轴上找一点C,使得|AC-BC|的 值最大,则此时点C的坐标为 .(-4,0)解析 如图所示,连接AB并延长交x轴于点C, 此时|AC-BC|的值最大,为AB的长,点C为所求的点.设直线AB 的解析式为y=kx+b(k≠0),把A(2,3),B(0,2)代入,得 解得 故直线AB的解析式为y= x+2.令y= x+2=0,则x=-4,故点C的坐标为(-4,0).故答案为(-4,0).19.(6分)若y-2与2x+3成正比例,且当x=1时,y=12.(1)求y与x的函数解析式.(2)求当y=4时,x的值.三、解答题(共6小题,共46分)解析 (1)设y-2=k(2x+3),把x=1,y=12代入,得12-2=5k,解得k=2,所以y-2=2(2x+3),所以y与x之间的函数关系式为y=4x+8.(2)当y=4时,4x+8=4,解得x=-1.20.(跨学科·物理)(7分)世界上大部分国家都使用摄氏温度, 少数国家使用华氏温度.两种计量之间有如下对应.(1)如果两种计量之间的关系是一次函数关系,设摄氏温度为 x(℃)时对应的华氏温度为y(°F),请你写出华氏温度关于摄氏 温度的函数表达式.(2)当华氏温度为0°F时,摄氏温度是多少℃?(3)华氏温度的值与对应的摄氏温度的值有可能相等吗?若可 能,求出此值;若不可能,请说明理由.解析 (1)设华氏温度y(°F)与摄氏温度x(℃)之间的函数关系 式为y=kx+b(k≠0),把(0,32),(10,50)代入,得 解得 ∴华氏温度y(°F)与摄氏温度x(℃)之间的函数关系式为y=1.8 x+32.(2)当y=0时,0=1.8x+32,解得x=- ,故当华氏温度为0°F时,摄氏温度是- ℃.(3)华氏温度的值与对应的摄氏温度的值有可能相等.当y=x 时,x=1.8x+32,解得x=-40.∴当华氏温度为-40 °F时,摄氏温度是-40 ℃.21.(7分)画出一次函数y=-2x+3的图像,根据图像解决下列问 题.(1)写出直线上横坐标是2的点的坐标.(2)写出y>0时,x的取值范围.(3)写出直线上到x轴的距离等于4的点的坐标.解析 直线y=-2x+3过点(0,3)、(1.5,0),如图. (1)如图,直线上横坐标是2的点的坐标是(2,-1).(2)由图像可得y>0时,x的取值范围是x<1.5.(3)当y=4时,4=-2x+3,解得x=-0.5,当y=-4时,-4=-2x+3,解得x=3.5,即直线上到x轴的距离等于4的点的坐标是(-0.5,4)或(3.5,-4).22.(教材变式·P138T1)(8分)【问题情境】“漏壶”是一种古 代计时器,在社会实践活动中,某小组同学根据“漏壶”的原 理制作了如图①所示的液体漏壶,漏壶可看成是由一个圆锥 和一个圆柱组成的,中间连通,液体可以从圆锥容器中匀速漏 到圆柱容器中,实验开始时圆柱容器中已有一部分液体.【实验观察】(1)下表是实验记录的圆柱体容器液面高度y (厘米)与时间x(小时)的数据:请你利用数据画出图像.【探索发现】(2)请你根据表中的数据及图像,用所学过的函 数的知识确定y与x之间的函数解析式.【结论应用】(3)如果本次实验记录的开始时间是上午9:00, 那么当圆柱容器中液面高度达到12厘米时是几点?解析 (1)描出各点,并连接,如图. (2)由(1)中的图像可知该函数为一次函数,设该函数的表达式 为y=kx+b(k≠0),∵点(1,6),(2,10)在该函数图像上,∴ 解得 ∴y与x的函数表达式为y=4x+2.(3)当y=12时,即4x+2=12,解得x=2.5,9+2.5=11.5,即圆柱容器中 液面高度达到12厘米时是上午11:30.23.(2023四川成都中考)(8分)2023年7月28日至8月8日,第31 届世界大学生运动会在成都举行.“当好东道主,热情迎嘉 宾”,成都某知名小吃店计划购买A,B两种食材制作小吃.已 知购买1千克A种食材和1千克B种食材共需68元,购买5千克A 种食材和3千克B种食材共需280元.(1)求A,B两种食材的价格.(2)该小吃店计划购买两种食材共36千克,其中购买A种食材 千克数不少于B种食材千克数的2倍,当A,B两种食材分别购 买多少千克时,总费用最少?并求出最少总费用.解析 (1)设A种食材的价格为x元/千克,B种食材的价格为y 元/千克.根据题意,得 解得 答:A种食材的价格是每千克38元,B种食材的价格是每千克30元.(2)设A种食材购买m千克,总费用为w元,则B种食材购买(36 -m)千克.根据题意,得w=38m+30(36-m)=8m+1 080.∵m≥2(36-m),∴24≤m<36.∵k=8>0,∴w随m的增大而增大,∴当m=24时,w有最小值,为8×24+1 080=1 272(元),∴A种食材购买24千克,B种食材购买12千克时,总费用最少, 为1 272元.24.(新考向·过程性学习试题)(10分)【直观想象】如图1,动点P在数轴上从负半轴向正半轴运动, 点P到原点的距离先变小再变大,当点P的位置确定时,点P到 原点的距离也确定.【数学发现】当一个动点P(x,0)到一个定点的距离为d时,我 们发现d是x的函数.【数学理解】(1)动点P(x,0)到定点A(2,0)的距离为d,当x= 时,d取最小值.【类比迁移】(2)设动点P(x,0)到两个定点M(1,0)、N(3,0)的距离和为y.①随着x增大,y怎样变化?②在图2的平面直角坐标系中画出y关于x的函数图像.③当y>6时,x的取值范围是 . 图1 图2解析 (1)当A,P重合时,d最小,为0,此时x=2.故答案为2.(2)①当x<1时,随着x增大,y变小;当1≤x≤3时,随着x增大,y不 变;当x>3时,随着x增大,y变大.②如图.③观察图像可知,满足条件的x的取值范围为x<-1或x>5.故答 案为x<-1或x>5.
相关资料
更多









