苏科版初中八年级数学上册期中素养综合测试课件

这是一份苏科版初中八年级数学上册期中素养综合测试课件，共60页。

一、选择题(每题3分,共8小题,共24分)1.下列说法不正确的是 (　　)A.如果两个图形全等,那么它们的形状和大小一定相同B.全等三角形的对应边相等,对应角相等C.图形全等,只与形状、大小有关,而与它们的位置无关D.面积相等的两个图形是全等图形
解析　面积相等的两个图形不一定是全等图形,原说法错误, 符合题意.故选D.
2.(跨学科·化学)(2023湖南衡阳中考)下面四种化学仪器的示 意图是轴对称图形的是 (　　) A　     B　     C　     D
3.如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是 四条边的中点,为了稳固,需要在窗框上钉一根木条,这根木 条不应钉在 (　　) A.G,H两点处　    B.A,C两点处C.E,G两点处　    D.B,F两点处
解析　这根木条不应钉在E、G两点处(没有构成三角形),这 种做法根据的是三角形的稳定性.故选C.
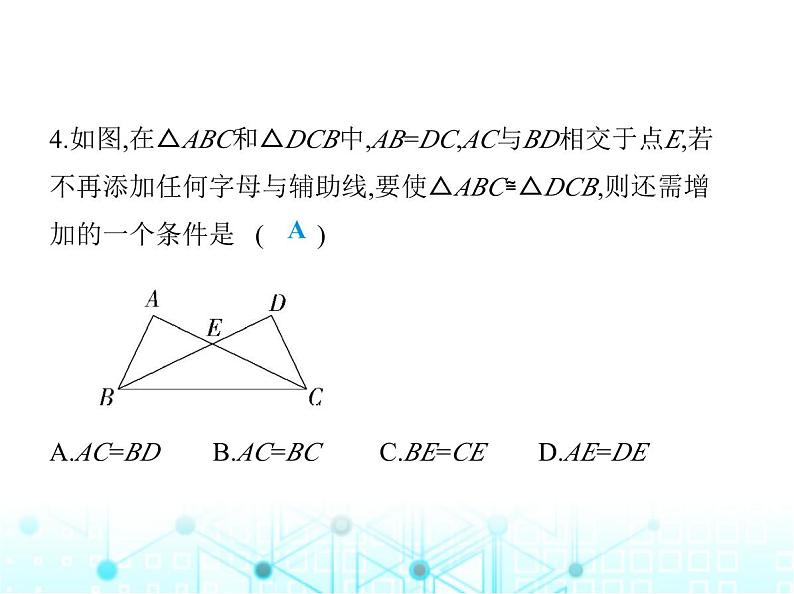
4.如图,在△ABC和△DCB中,AB=DC,AC与BD相交于点E,若 不再添加任何字母与辅助线,要使△ABC≌△DCB,则还需增 加的一个条件是 (　　) A.AC=BD　    B.AC=BC C.BE=CE　    D.AE=DE
解析　∵AB=DC,BC=CB,∴当添加AC=BD时,根据“SSS” 可判定△ABC≌△DCB.故选A.
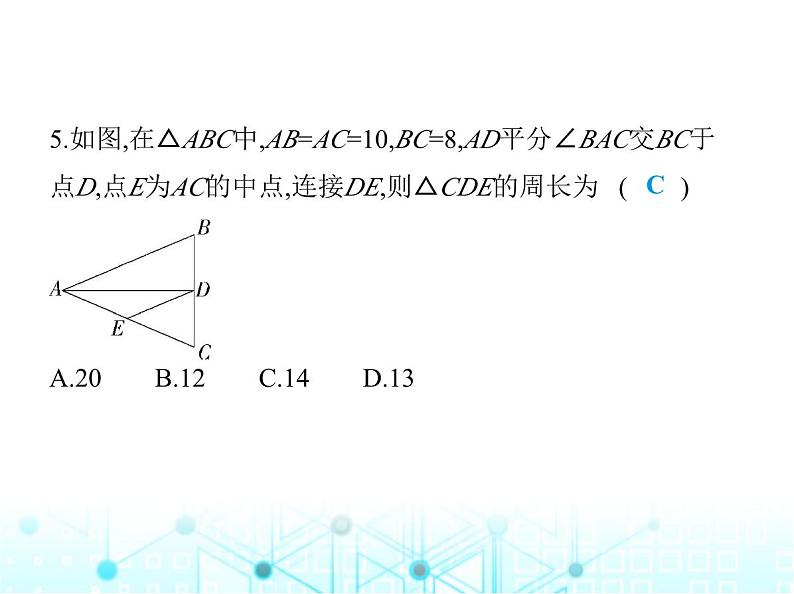
5.如图,在△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于 点D,点E为AC的中点,连接DE,则△CDE的周长为 (　　) A.20　    B.12　    C.14　    D.13
解析　∵AB=AC,AD平分∠BAC,BC=8,∴AD⊥BC,CD=BD= BC=4.∵点E为AC的中点,∴DE=CE= AC=5,∴△CDE的周长为CD+DE+CE=4+5+5=14.故选C.
6.一张正方形纸片经过两次对折,并在如图所示的位置剪去 一个小正方形,打开后的图形是 (　　) A　     B　     C　     D
解析　取一张与题中相同的纸片按照题目中的要求操作,可 得D选项中的图形.
7.如图,线段AB,BC的垂直平分线l1,l2交于点O,若∠1=30°,则 ∠AOC的度数是 (　　) A.50°　    B.60°　    C.70°　    D.80
解析　如答图,连接OB,设直线l1与AB相交于点D,直线l2与BC 相交于点E. ∵∠1=30°,∴∠DOE=180°-∠1=150°,∴∠DOB+∠BOE=150°.
∵线段AB,BC的垂直平分线l1,l2交于点O,∴OA=OB,OB=OC,OD⊥AB,OE⊥BC,∴∠AOB=2∠DOB,∠BOC=2∠BOE,∴∠AOB+∠BOC=2∠DOB+2∠BOE=2(∠DOB+∠BOE)=30 0°,∴∠AOC=360°-(∠AOB+∠BOC)=360°-300°=60°.故选B.
8.如图,△ABC中,AC=DC=3,BD垂直∠BAC的平分线于D,E为AC的中点,则图中两个阴影部分面积之差的最大值为 (    　) A.6　    B.4.5　    C.3　    D.2
解析　延长BD,AC相交于点H.设AD交BE于点O. ∵AD⊥BH,∴∠ADB=∠ADH=90°,∴∠ABD+∠BAD=90°,∠ H+∠HAD=90°.∵∠BAD=∠HAD,∴∠ABD=∠H,∴AB=AH.
CH=AC.∵AE=EC,∴S△ABE= S△ABH,S△CDH= S△ABH.∴S△OBD-S△AOE=S△ADB-S△ABE=S△ADH-S△CDH=S△ACD,∵AC=CD=3,∴当DC⊥AC时, △ACD的面积最大,最大面积为 ×3×3=4.5.故选B.
∵AD⊥BH,∴BD=DH.∵DC=CA,∴∠CDA=∠CAD.∵∠ CAD+∠H=90°,∠CDA+∠CDH=90°,∴∠CDH=∠H,∴CD=
9.如图,在△ABC中,∠ACB=90°,AB=6,点D为斜边AB的中点, 则CD的长为　　　    .
二、填空题(每题3分,共10小题,共30分)
10.已知△ABC是等腰三角形,若∠A=60°,则△ABC有　  条对称轴.
解析　∵△ABC是等腰三角形,∠A=60°,∴△ABC是等边三角形,∴△ABC有3条对称轴.故答案为3.
11.如图,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据 “HL”判定,还需要添加条件:　　 　    .
AB=AC(答案不唯一)
解析　答案不唯一.如:添加条件AB=AC.∵AD⊥BC于D,∴∠ADB=∠ADC=90°.在Rt△ABD和Rt△ACD中, ∴Rt△ABD≌Rt△ACD(HL).
12.(新考向·尺规作图)如图,在△ABC中,AB=AC,∠CBA=54°, 以点C为圆心,CA的长为半径作弧交AB于点D,分别以点A和 点D为圆心,大于 AD的长为半径作弧,两弧相交于点E,作直线CE,交AB于点F,则∠ACF的度数是　　　    .
解析　由作图可得CF⊥AB于F,∴∠BFC=90°,∴∠BCF=90° -∠CBA=36°,∵AB=AC,∠CBA=54°,∴∠ACB=∠CBA=54°,∴ ∠ACF=54°-36°=18°.故答案为18°.
13.(2023江苏淮安洪泽期中)如图,点P为∠AOB内部任意一 点,点P与点P1关于OA对称,点P与点P2关于OB对称,OP=4,∠AOB=45°,则△OP1P2的面积为　　　    .
解析　∵点P1和点P关于OA对称,点P2和点P关于OB对称,∴OP1=OP=OP2=4,∠AOP1=∠AOP,∠BOP=∠BOP2,∴∠P1OP2=2∠AOP+2∠BOP=2∠AOB=90°,∴△P1OP2是直角三角形,∴△OP1P2的面积为 ×4×4=8.故答案为8.
14.如图,直线a,b交于点O,∠α=60°,点A是直线a上的一个定 点,点B在直线b上运动,若以点O,A,B为顶点的三角形是等腰 三角形,则∠OAB=　　　    .　
解析　如图1,当点B在OA上方时,根据题意,得∠AOB=60°.∵△OAB是等腰三角形,∴△OAB是等边三角形,∴∠OAB=60°.
图1 图2
 如图2,当点B在OA下方时,OA=OB,∴∠OBA=∠OAB.∵∠OBA+∠OAB=∠α=60°,∴∠OAB=30°.故答案为60°或30°.
15.如图,分别以直角三角形各边为边向三角形外部作正方 形,其中两个正方形的面积分别为26和10,则正方形A的面积 是　　　    .
解析　如图, 由题意知BD2=26,BC2=10,且∠DCB=90°,∴CD2=BD2-BC2=26-10=16.∴正方形A的面积为CD2=16.故答案为16.
16.(2024江苏南京江宁期中)把长方形纸片ABCD按如图所示 的方式折叠,使顶点B和D重合,折痕为EF,若AB=3 cm,BC=5 cm,则线段DE=　　　    cm. 
解析　∵AB=3 cm,BC=5 cm,∴A'D=AB=3 cm,设AE=x cm,则A'E=x cm,DE=(5-x)cm,在Rt△A'DE中,A'E2+A'D2=ED2,∴x2+9=(5-x)2,解得x=1.6,∴DE=5-1.6=3.4 cm.故答案为3.4.
17.如图,在锐角△ABC中,∠B=30°,AC=4,S△ABC=16,P是边AC 上的一动点,点P关于直线AB、BC的对称点分别是D、E,连 接DE,则DE的最小值为　　　    .
解析　如图,连接BD,BP,BE,PD,PE. ∵点P关于直线AB、BC的对称点分别是D、E,∴AB垂直平分PD,BC垂直平分PE,∴BD=BP,BE=BP,∴∠PBD=2∠PBA,∠PBE=2∠PBC,
∴∠DBE=∠PBD+∠PBE=2(∠PBA+∠PBC)=2∠ABC=60°, ∴△BDE是等边三角形,∴DE=BD=BP.当BP⊥AC时,BP的值最小,此时△BAC的面积= AC·BP=16.∵AC=4,∴BP=8,∴DE的最小值为8.故答案为8.
18.若一个四位数M的个位数字与十位数字的平方和恰好是 M去掉个位数字与十位数字后得到的两位数,则这个四位数 M为“勾股和数”.如:M=2 543,∵32+42=25,∴2 543是“勾股 和数”.(1)判断2 022,2 023,2 024中是“勾股和数”的是　　　    .(2)一个“勾股和数”M的千位数字为a,百位数字为b,十位数 字为c,个位数字为d,若c+d=9,c≠0,当 为整数时,M是　　　　 　　　    .
8 190或4 536或4 563
解析　(1)∵22+22=8,8≠20,∴2 022不是“勾股和数”.∵22+32=13,13≠20,∴2 023不是“勾股和数”.∵22+42=20,∴2 024是“勾股和数”.故答案为2 024.(2)∵M为“勾股和数”,∴10a+b=c2+d2,∴9∴cd能被3整除.∵c≠0,∴①c=9,d=0,此时M=8 190,②c=3,d=6或c=6,d=3,此时M=4 536或4 563.∴M的值为8 190或4 536或4 563.故答案为8 190或4 536或4 5 63.
19.[答案含评分细则] (2023四川泸州中考)(10分)如图,点B在 线段AC上,BD∥CE,AB=EC,DB=BC.求证:AD=EB. 
三、解答题(共6小题,共66分)
证明　∵BD∥CE,∴∠ABD=∠C. 3分在△ABD和△ECB中, ∴△ABD≌△ECB(SAS), 8分∴AD=EB. 10分
20.[答案含评分细则](情境题·现实生活)(10分)如图,有两个 长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的 长度DF相等,请猜想两个滑梯的倾斜角∠ABC和∠DFE的度 数和为多少,并证明你的结论.
解析　∠ABC+∠DFE=90°. 2分证明:由题意可得,△ABC与△DEF均是直角三角形,且BC= EF,AC=DF. 3分在Rt△ABC和Rt△DEF中, ∴Rt△ABC≌Rt△DEF(HL), 6分∴∠ABC=∠DEF. 7分∵∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°. 10分
21.[答案含评分细则] (10分)如图,在正方形网格中,每个小正 方形的边长都是1,每个小正方形的顶点叫做格点.网格中有 一个格点△ABC(即三角形的顶点都在格点上).(1)在图中作出△ABC关于直线l对称的△A1B1C1(要求A与A1, B与B1,C与C1相对应).(2)求△ABC的面积.(3)在直线l上找一点P,使得△PAC的周长最小.
解析　(1)如图,△A1B1C1即为所求作的图形. 4分(2)△ABC的面积为3×4- ×2×3- ×2×2- ×1×4=5. 7分(3)如图,点P即为所求作的点. 10分 
22.[答案含评分细则] (2024江苏镇江润州期中)(10分)如图,在 △ABC中,AB的垂直平分线分别交AB,AC及BC的延长线于点 D,E,F,且CB2=AE2-CE2.(1)求证:∠ACB=90°.(2)若AC=12,BC=9,求CE的长.
解析　(1)证明:连接BE,如图: ∵ED垂直平分AB,∴AE=BE. 1分∵CB2=AE2-CE2,∴CB2=BE2-CE2,∴CB2+CE2=BE2,∴△BEC是直角三角形,
∴∠ACB=90°. 5分(2)设CE=x,则AE=12-x, 6分∵BE=AE,∴BE=12-x.∵BC=9,CB2+CE2=BE2,∴92+x2=(12-x)2, 9分解得x= .即CE= . 10分
23.[答案含评分细则] (2023江苏苏州中考)(12分)如图,在△ ABC中,AB=AC,AD为△ABC的角平分线.以点A为圆心,AD长 为半径画弧,与AB,AC分别交于点E,F,连接DE,DF.(1)求证:△ADE≌△ADF.(2)若∠BAC=80°,求∠BDE的度数.
解析　(1)证明:∵AD是△ABC的角平分线,∴∠BAD=∠CAD. 1分由作图知AE=AF. 2分在△ADE和△ADF中, ,∴△ADE≌△ADF(SAS). 6分(2)∵∠BAC=80°,AD为△ABC的角平分线,∴∠EAD= ∠BAC=40°. 7分
由作图知AE=AD.∴∠AED=∠ADE,∴∠ADE= ×(180°-40°)=70°. 9分∵AB=AC,AD为△ABC的角平分线,∴AD⊥BC.∴∠BDE=90°-∠ADE=20°. 12分
24.[答案含评分细则] (半角模型)(14分)半角模型是指有公共 顶点,较小角等于较大角的一半,且组成这个较大角的两边相 等的一类模型.通过翻折或旋转,将角的倍分关系转化为角的 相等关系,并进一步构造全等三角形,解决相应问题.(1)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC= 90°,E、F分别是BC、CD上的点,且∠EAF=60°.在探究图1中 线段BE,EF,FD之间的数量关系时,可延长CD至点G,使得DG =BE,连接AG,进而通过证明三角形全等来探究线段BE,EF,
FD之间的数量关系.请写出线段BE,EF,FD之间的数量关系, 并说明理由.(2)探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分 别是BC、CD上的点,且∠EAF= ∠BAD,(1)中的结论是否仍然成立?请说明理由.(3)结论应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30
°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指 挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60 海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E、F处,且∠EOF=70°,试求此时两舰艇之间的距离.(4)能力提高:如图4,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M、N 在边BC上,且∠MAN=45°,若BM=3,CN=4,试求出MN的长.
图1 图2 图3 图4
解析　(1)EF=BE+DF.理由:∵∠ADC=90°,∴∠ADG=90°,∴∠ADG=∠B,在△ABE和△ADG中, ∴△ABE≌△ADG(SAS), 2分∴AE=AG,∠BAE=∠DAG.∵∠EAF= ∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF= ∠EAF,在△AEF和△AGF中, ∴△AEF≌△AGF(SAS), 3分∴EF=FG.∵FG=DG+DF=BE+DF,∴EF=BE+DF. 4分(2)(1)中的结论仍然成立,即EF=BE+DF.
理由:如图,延长FD到点G,使DG=BE,连接AG. ∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,∴∠B=∠ADG,在△ABE和△ADG中, ∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG. 5分∵∠EAF= ∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF= ∠EAF,在△AEF和△AGF中, ∴△AEF≌△AGF(SAS), 6分∴EF=FG.
∵FG=DG+DF=BE+DF,∴EF=BE+DF. 7分(3)如图,连接EF,延长AE、BF相交于点C. 
∵∠AOB=30°+90°+(90°-70°)=140°,∠EOF=70°,∴∠EOF= ∠AOB. 8分∵OA=OB,∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°,∴符合探索延伸中的条件,∴结论EF=AE+BF成立, 9分即EF=1.5×(60+80)=210(海里).∴此时两舰艇之间的距离为210海里. 10分(4)如图,作CD⊥BC,使CD=BM,连接AD,DN.
 ∵△ABC是等腰直角三角形,AB=AC,∠BAC=90°,∴∠ABM=∠BCA=45°,∴∠ACD=∠BCD-∠BCA=90°-45°=45°,∴∠ABM=∠ACD.在△ABM和△ACD中, 
∴△ABM≌△ACD(SAS), 11分∴AM=AD,∠BAM=∠CAD,∴∠DAN=∠CAD+∠CAN=∠BAM+∠CAN=90°-∠MAN=45°. 12分在△MAN和△DAN中, ∴△MAN≌△DAN(SAS),∴MN=DN. 13分