




初中数学苏科版八年级上册1.3 探索三角形全等的条件图片ppt课件
展开知识点3 基本事实“角边角(ASA)”的推论“角角边(AAS)”
1.(2023江苏常州金坛期中)如图,OB平分∠AOC,点D、E、F分别是射线OA、OB、OC上的点,连接DE、EF,添加下列条件中的某一个,能使得△DOE≌△FOE成立,这个条件是 ( )
A.OD=OE B.OE=OF C.∠ODE=∠OED D.∠ODE=∠OFE
解析 ∵OB平分∠AOC,∴∠DOE=∠FOE.添加OD=OE不 能得到△DOE≌△FOE,故选项A不符合题意;添加OE=OF不 能得到△DOE≌△FOE,故选项B不符合题意;添加∠ODE= ∠OED不能得到△DOE≌△FOE,故选项C不符合题意;添加 ∠ODE=∠OFE,根据AAS可得△DOE≌△FOE,故选项D符 合题意.故选D.
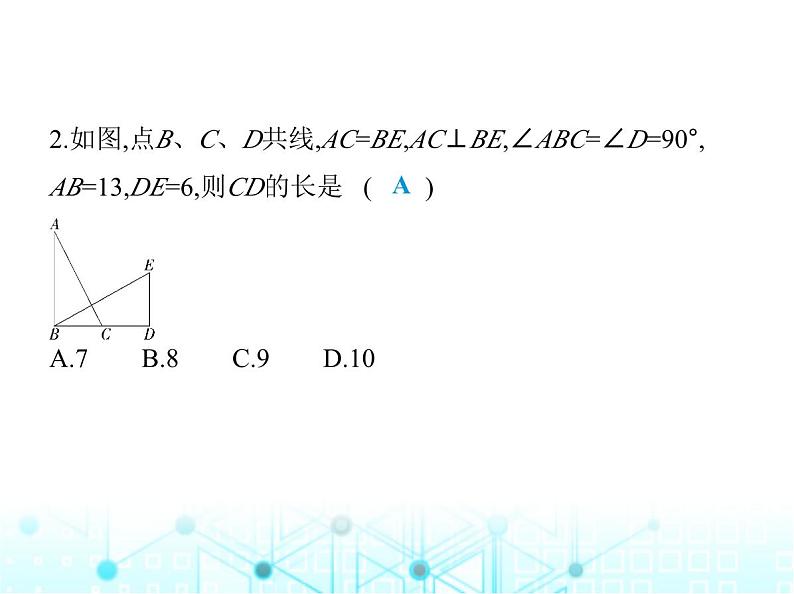
2.如图,点B、C、D共线,AC=BE,AC⊥BE,∠ABC=∠D=90°, AB=13,DE=6,则CD的长是 ( ) A.7 B.8 C.9 D.10
解析 ∵AC⊥BE,∠ABC=∠D=90°,∴∠A+∠ABE=∠ABE+ ∠EBD=90°,∴∠A=∠EBD.在△ABC与△BDE中, ∴△ABC≌△BDE(AAS),∴BC=DE=6,AB=BD=13,∴CD=BD -BC=13-6=7.故选A.
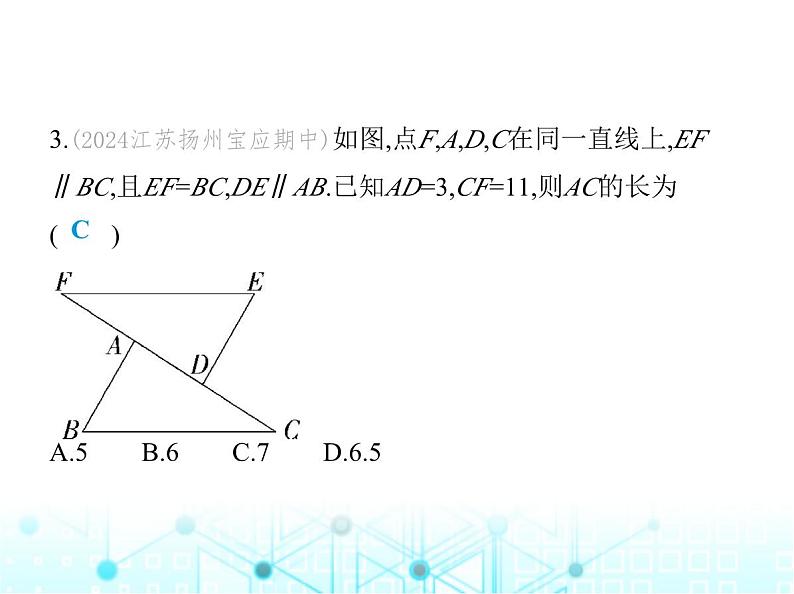
3.(2024江苏扬州宝应期中)如图,点F,A,D,C在同一直线上,EF ∥BC,且EF=BC,DE∥AB.已知AD=3,CF=11,则AC的长为 ( ) A.5 B.6 C.7 D.6.5
解析 ∵EF∥BC,∴∠F=∠C.∵DE∥AB,∴∠EDF=∠BAC. ∵EF=BC,∴△ABC≌△DEF(AAS),∴AC=FD,∴CD=AF.∵ AD=3,CF=11,∴CD+AF=CF-AD=8,∴CD=4,∴AC=AD+CD= 3+4=7.故选C.
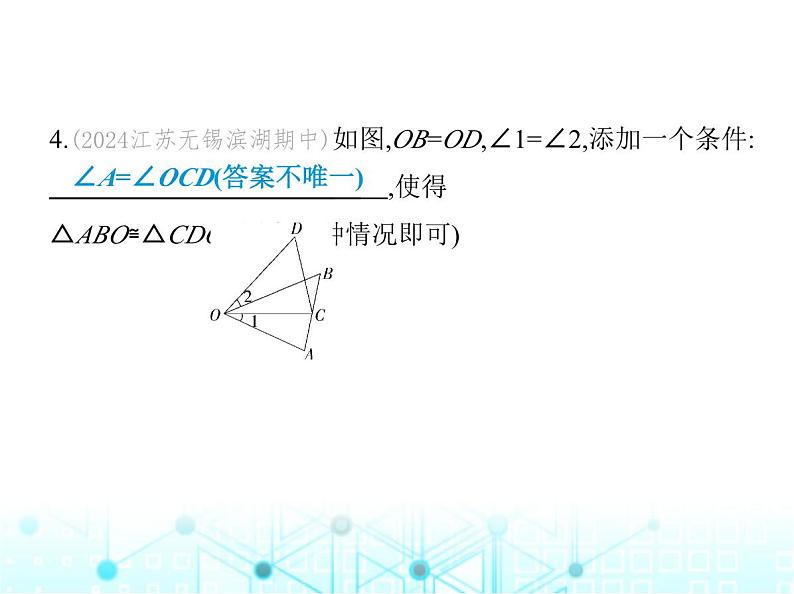
4.(2024江苏无锡滨湖期中)如图,OB=OD,∠1=∠2,添加一个条件: ,使得△ABO≌△CDO.(写出一种情况即可)
∠A=∠OCD(答案不唯一)
解析 答案不唯一.如添加∠A=∠OCD.∵∠1=∠2,∴∠1+∠BOC=∠2+∠BOC,即∠AOB=∠COD.∵ OB=OD,∠A=∠OCD,∴△ABO≌△CDO.
5.(2024江苏泰州兴化月考)如图,在四边形ABEF中,AB=4,EF =6,点C是BE上一点,连接AC、CF,若AC=CF,∠B=∠E=∠ ACF,则BE的长为 .
解析 ∵∠B+∠BAC=∠ACE=∠FCE+∠ACF,∠B=∠ACF, ∴∠BAC=∠FCE.在△ABC和△CEF中, ∴△ABC≌△CEF(AAS),∴AB=CE,BC=EF.∵AB=4,EF=6,∴CE=4,BC=6,∴BE=BC+ CE=6+4=10.故答案为10.
6.(一线三等角模型)王强同学用10块高度都是2 cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 cm.
解析 根据题意,得AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°,∵∠ACB=90°,∠ADC=90°,∴∠ACD+∠BCE=90°,∠ACD+ ∠DAC=90°,∴∠BCE=∠DAC.在△ADC和△CEB中, ∴△ADC≌△CEB(AAS).∴AD=EC=6 cm,DC=BE=14 cm,∴DE=DC+CE=20 cm.故答案为20.
7.(2023四川乐山中考)如图,已知AB与CD相交于点O,AC∥ BD,AO=BO.求证:AC=BD.
证明 ∵AC∥BD,∴∠A=∠B,∠C=∠D.在△AOC和△BOD中, ∴△AOC≌△BOD(AAS),∴AC=BD.
8.(2024江苏泰州泰兴期末)如图,点E在△ABC的边AC上,AE= BC,BC∥AD,∠CED=∠BAD.求证:△ABC≌△DEA.
证明 ∵BC∥AD,∴∠DAC=∠C.∵∠CED=∠BAD,∠CED=∠D+∠DAC,∠BAD=∠DAC+∠ BAC,∴∠D=∠BAC.在△ABC和△DEA中, ∴△ABC≌△DEA(AAS).
9.(2022广东中考)如图,已知∠AOC=∠BOC,点P在OC上,PD ⊥OA,PE⊥OB,垂足分别为D,E.求证:△OPD≌△OPE.
证明 ∵PD⊥OA,PE⊥OB,∴∠ODP=∠OEP=90°.∵∠AOC=∠BOC,∴∠DOP=∠EOP.在△OPD和△OPE中, ∴△OPD≌△OPE(AAS).
10.(2023四川凉山州中考,9,★☆☆)如图,点E、点F在BC上, BE=CF,∠B=∠C,添加一个条件,不能证明△ABF≌△DCE的 是 ( )
A.∠A=∠D B.∠AFB=∠DECC.AB=DC D.AF=DE
解析 ∵BE=CF,∴BE+EF=CF+EF,即BF=CE,当∠A=∠D时,利用AAS可得△ABF≌△DCE,故A不符合题 意;当∠AFB=∠DEC时,利用ASA可得△ABF≌△DCE,故B不符 合题意;当AB=DC时,利用SAS可得△ABF≌△DCE,故C不符合题意;当AF=DE时,无法证明△ABF≌△DCE,故D符合题意.故选D.
11.(2024江苏宿迁宿城期中,5,★☆☆)如图,在四边形ABCD 中,AB∥DC,E为BC的中点,连接DE,AE,AE⊥DE,延长DE交 AB的延长线于点F.若AB=5,CD=2,则AD的长为 ( ) A.5 B.9 C.7 D.11
解析 ∵E为BC的中点,∴BE=EC.∵AB∥CD,∴∠F=∠ CDE.在△BEF与△CED中, ∴△BEF≌△CED(AAS),∴EF=DE,BF=CD=2,∴AF=AB+BF=7.∵AE⊥DE,∴∠AED=∠AEF=90°,又∵AE= AE,EF=DE,∴△AEF≌△AED,∴AF=AD=7.故选C.
12.(2024江苏泰州靖江月考,14,★☆☆)如图,四边形ABCD中, AB=BC,∠ABC=90°,对角线BD⊥CD,若BD=14,则△ABD的面 积为 .
解析 如图,过点A作AE⊥BD,垂足为E. ∵AE⊥BD,CD⊥BD,∴∠AEB=∠CDB=90°,∴∠BAE+∠ABE=90°.∵∠ABC=90°,∴∠ABD+∠DBC=90°, ∴∠BAE=∠DBC.∵AB=BC,∴△ABE≌△BCD(AAS),∴AE= BD=14,∴△ABD的面积= BD·AE= ×14×14=98.故答案为98.
13.(分类讨论思想)(2024江苏淮安淮阴期中,22,★★★)如图, 在△ABC中,∠ACB=90°,AC=7 cm,BC=3 cm,CD为AB边上的 高,点E从点B出发,在直线BC上以2 cm/s的速度朝固定方向匀 速移动,过点E作直线BC的垂线交直线CD于点F,当点E运动 s时,CF=AB.
解析 ∵∠ACB=90°,∴∠A+∠CBD=90°.∵CD为AB边上的高,∴∠CDB=90°,∴∠BCD+∠CBD=90°,∴∠A=∠BCD.∵∠BCD=∠ECF,∴∠ECF=∠A,∵EF⊥直线BC,∴∠CEF=90°=∠ACB.在△CEF和△ACB中, ,∴△CEF≌△ACB(AAS),∴CE=AC=7 cm.
①如图,当点E在射线BC上移动时,BE=CE+BC=7+3=10(cm), ∵点E从点B出发,在直线BC上以2 cm/s的速度移动,∴E移动 了10÷2=5(s).
②如图,当点E在射线CB上移动时,BE'=CE'-BC=7-3=4(cm).∵ 点E从点B出发,在直线BC上以2 cm/s的速度移动,∴E移动了 4÷2=2(s).综上所述,当点E运动5 s或2 s时,CF=AB.故答案为2或5.
14.(2024江苏盐城建湖期中,21,★☆☆)如图,点D、E分别在 AB、AC上,AD=AE,BE、CD相交于点O,∠B=∠C.求证:(1)△ABE≌△ACD.(2)△BOD≌△COE.
证明 (1)在△ABE和△ACD中, ∴△ABE≌△ACD(AAS).(2)∵△ABE≌△ACD,∴AB=AC.∵AD=AE,∴BD=CE.在△BOD和△COE中, ∴△BOD≌△COE(AAS).
15.(情境题·现实生活)(2024江苏泰州泰兴期中,24,★★☆)小丽与爸爸妈妈在公园里荡秋千,如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1.2 m高的B处接住她后用力一推,爸爸在C处接住她,若妈妈与爸爸到OA的水平距离BF、CG分别为1.8 m和2.2 m,∠BOC=90°.(1)△CGO与△OFB全等吗?请说明理由.(2)爸爸是在距离地面多高的地方接住小丽的?
解析 (1)△OCG与△BOF全等.理由:由题意可知∠CGO=∠BFO=90°,OB=OC.∴∠BOF+∠OBF=90°,∵∠BOC=90°,∴∠COG+∠BOF=90°.∴∠COG=∠OBF.在△CGO与△OFB中, ∴△CGO≌△OFB(AAS).
苏科版八年级上册1.3 探索三角形全等的条件课文ppt课件: 这是一份苏科版八年级上册<a href="/sx/tb_c17288_t3/?tag_id=26" target="_blank">1.3 探索三角形全等的条件课文ppt课件</a>,共28页。
初中数学苏科版八年级上册1.3 探索三角形全等的条件教学ppt课件: 这是一份初中数学苏科版八年级上册<a href="/sx/tb_c17288_t3/?tag_id=26" target="_blank">1.3 探索三角形全等的条件教学ppt课件</a>,共26页。
初中数学人教版八年级上册12.2 三角形全等的判定教学ppt课件: 这是一份初中数学人教版八年级上册12.2 三角形全等的判定教学ppt课件,共45页。PPT课件主要包含了学习目标,新课引入,新知学习,课堂小结,SSS,SAS,△ABE≌△ACD,第1题图,第3题图,第4题图等内容,欢迎下载使用。













