青岛版初中八年级数学上册第1章素养综合检测课件

这是一份青岛版初中八年级数学上册第1章素养综合检测课件，共48页。

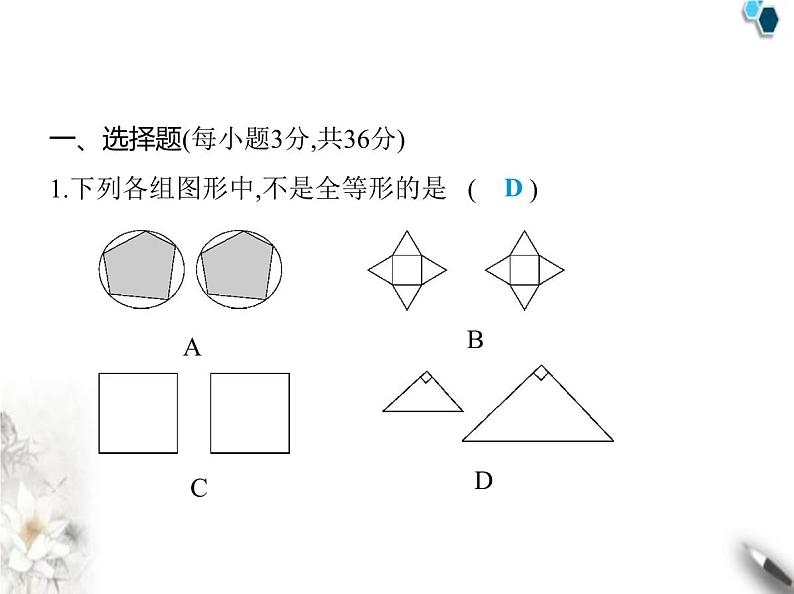
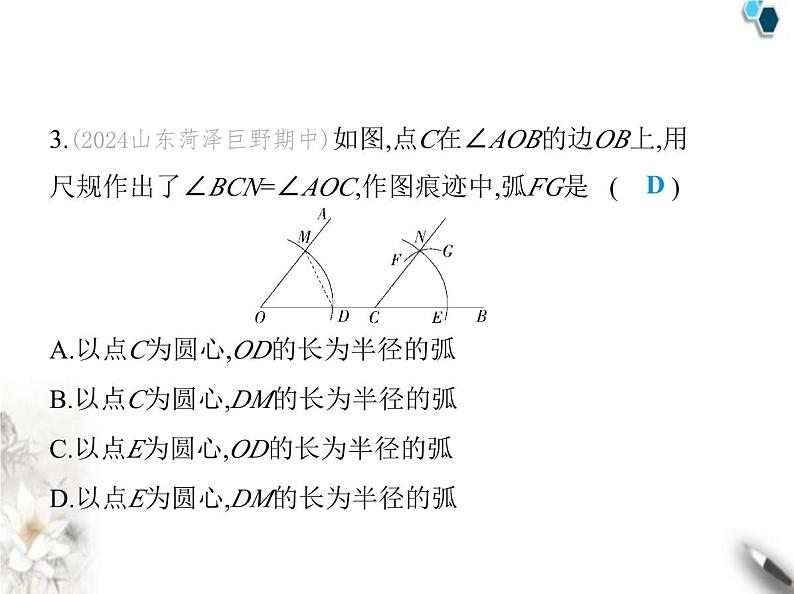
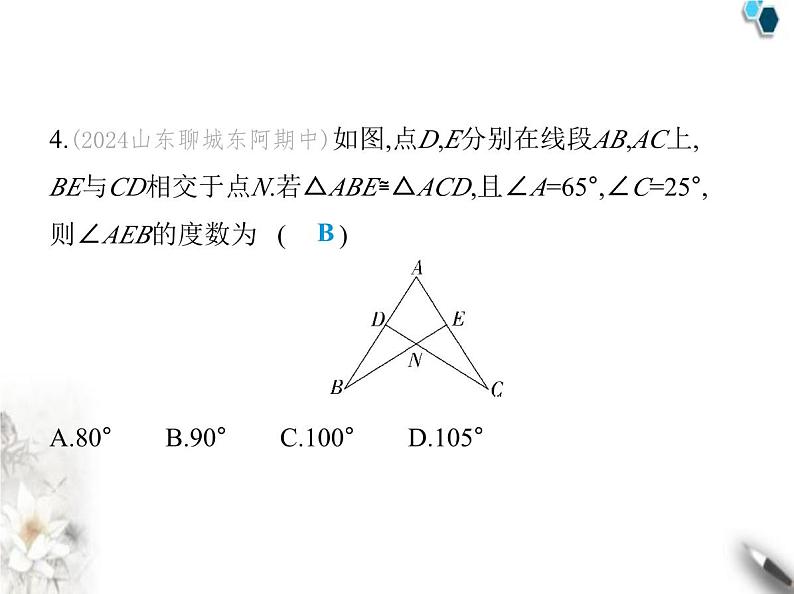
(满分100分, 限时60分钟)第1章　素养综合检测一、选择题(每小题3分,共36分)1.下列各组图形中,不是全等形的是 (　　)ABCDD解析　直接利用全等形的定义即可得出答案.D选项中的两个图形大小不相等,故不是全等形.故选D.2.(2023山东菏泽成武期中)下列结论中不正确的是 (　　)A.全等三角形的对应边相等B.全等三角形的面积相等C.全等三角形的周长相等D.周长相等的两个三角形全等D解析　周长相等的两个三角形不一定全等,故D错误,符合题意.故选D.3.(2024山东菏泽巨野期中)如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC,作图痕迹中,弧FG是 (　　)A.以点C为圆心,OD的长为半径的弧B.以点C为圆心,DM的长为半径的弧C.以点E为圆心,OD的长为半径的弧D.以点E为圆心,DM的长为半径的弧D解析　根据作一个角等于已知角的尺规作图步骤,可得弧FG是以点E为圆心,DM的长为半径的弧.故选D.4.(2024山东聊城东阿期中)如图,点D,E分别在线段AB,AC上,BE与CD相交于点N.若△ABE≌△ACD,且∠A=65°,∠C=25°,则∠AEB的度数为 (　　) A.80°　    B.90°　    C.100°　    D.105°B解析　在△ACD中,因为∠A+∠ADC+∠C=180°,所以∠ADC=180°-∠A-∠C=90°.因为△ABE≌△ACD,所以∠AEB=∠ADC=90°,故选B.5.(新独家原创)如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,CD∥AB,则△CFD≌△BEA的依据是 (　　)A.SAS　    B.ASA C.AAS　    D.SSS    B解析　因为CD∥AB,所以∠C=∠B.因为CE=BF,所以CE-EF=BF-EF,所以CF=BE.又因为∠CFD=∠BEA,所以△CFD≌△BEA(ASA),故选B.6.(2024山东聊城冠县期中)根据下列已知条件,能画出唯一的△ABC的是 (　　)A.∠C=90°,AB=6 B.AB=4,BC=3,∠A=30°C.∠A=60°,∠B=45°,AB=4 D.AB=3,BC=4,CA=8C解析　选项A只有两个条件,选项B不符合全等三角形的判定定理,选项D不满足三角形的三边关系,不能构成三角形,故选A、B、D不符合题意.选项C,满足ASA,能画出唯一的△ABC,故选C.7.(2024北京海淀外国语实验学校期中)如图所示,已知△ABC的五个元素,甲、乙、丙三个三角形和△ABC全等的是 (     )A.甲和乙　    B.乙和丙C.只有乙　    D.只有丙B解析　甲三角形不符合三角形全等的判定方法,所以甲三角形和△ABC不全等;乙三角形符合SAS,所以乙三角形和△ABC全等;丙三角形符合AAS,所以丙三角形和△ABC全等,故选B.8.(2024山东聊城阳谷期中)如图,EF=CF,BF=DF,则下列结论中不一定正确的是 (　　)A.△BEF≌△DCF　    B.△ABC≌△ADEC.AB=AD　     D.DC=ACD解析　在△BEF和△DCF中, 所以△BEF≌△DCF(SAS),选项A中结论正确,不合题意;因为△BEF≌△DCF,所以∠B=∠D.因为BF=DF,EF=CF,所以BF+CF=DF+EF,即BC=DE.在△ABC和△ADE中, 所以△ABC≌△ADE(AAS),选项B中结论正确,不合题意;因为△ABC≌△ADE,所以AB=AD,选项C中结论正确,不合题意;根据题中条件无法证出DC=AC,所以选项D中结论不一定正确,符合题意.故选D.9.(2024山东聊城莘县期中)三个全等三角形按如图所示的方式摆放,则∠1+∠2+∠3的度数是 (　　) A.90°　    B.120°　    C.135°　    D.180°D解析　如图,∠1+∠4+∠5=180°,∠8+∠6+∠2=180°,∠3+∠9+∠7=180°,所以∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=540°.因为三个三角形全等,所以∠4+∠9+∠6=180°,又因为∠5+∠7+∠8=180°,所以∠1+∠2+∠3+180°+180°=540°,所以∠1+∠2+∠3=180°,故选D.10.(2023北京大兴期末)如图,在四边形ABCD中,对角线AC,BD相交于点O,若AB=CD,AD=BC,则图中的全等三角形有 (　　) A.1对　    B.2对　    C.3对　    D.4对D解析　在△ABD和△CDB中, 所以△ABD≌△CDB(SSS),同理△ACD≌△CAB.因为△ABD≌△CDB,所以∠ABD=∠CDB,又因为∠AOB=∠COD,AB=CD,所以△AOB≌△COD(AAS),同理△AOD≌△COB.综上,题图中的全等三角形有4对,故选D.11.(2023浙江杭州期中)如图,AB⊥CD,且AB=CD.E、F是AD上的两点,CE⊥AD,BF⊥AD.若BF=a,EF=b,CE=c,则AD的长为 (　　) A.a+c　     B.b+cC.a-b+c　    D.a+b-cC解析　因为AB⊥CD,CE⊥AD,BF⊥AD,所以∠AFB=∠CED=90°,∠A+∠D=90°,∠C+∠D=90°,所以∠A=∠C.在△ABF与△CDE中, 所以△ABF≌△CDE(AAS),所以AF=CE=c,DE=BF=a,又因为EF=b,所以AD=AF+DF=AF+(DE-EF)=c+(a-b)=a-b+c.12.(新考向·尺规作图)如图,已知锐角∠AOB,根据以下要求作图:(1)在射线OA上取点C和点E,以点O为圆心,OC,OE的长为半径画弧,分别交射线OB于点D,F;(2)连接CF,DE,DE与CF交于点P.下列结论中错误的是 (　　)A.CE=DF B.点P在∠AOB的平分线上C.PE=PF D.若∠AOB=60°,则∠CPD=120°D解析　由作图,得OE=OF,OC=OD,所以OE-OC=OF-OD,即CE=DF,选项A中结论正确;在△EOD与△FOC中, 所以△EOD≌△FOC(SAS),所以∠OED=∠OFC,ED=FC.在△ECP与△FDP中, 所以△ECP≌△FDP(AAS),所以PE=PF,所以ED-PE=FC-PF,即PD=PC,连接OP(图略),在△OCP与△ODP中, 所以△OCP≌△ODP(SSS),所以∠COP=∠DOP,所以点P在∠AOB的平分线上,选项B、C中结论正确;因为△OCP≌△ODP,所以∠OCP=∠ODP,由∠AOB=60°,无法得到∠OCP=∠ODP=90°,所以无法得到∠CPD=120°,选项D中结论错误.故选D.二、填空题(每小题3分,共15分)13.(2024北京海淀外国语实验学校期中)如图,一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是　 　    　　 　    .的稳定性 三角形解析　一扇窗户打开后,用窗钩BC可将其固定(组成了三角形),所运用的几何原理是三角形的稳定性.14.(2020湖南怀化中考)如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=130°,则∠D=　　　    °.13015.(新考向·开放性试题)(2023黑龙江牡丹江中考)如图,AB∥CD,AD与BC交于点O,请添加一个条件　 　　　    ,使△AOB≌△DOC.(只填一种情况即可)    AB=DC(或AO=DO或OB=OC,答案不唯一)解析　答案不唯一.因为AB∥CD,所以∠A=∠D,∠B=∠C.若添加条件AB=DC,由ASA可判定△AOB≌△DOC;若添加条件AO=DO或OB=OC,由AAS可判定△AOB≌△DOC.16.(倍长中线模型)(2024山东潍坊高新区期中)如图,在△ABC中,AB=15,AC=9,D为边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.则边BC上的中线AD的取值范围是　　         .3”“<”或“=”填空).(2)探究AP与AQ的位置关系和数量关系.(3)若把(1)中的△ABC改为钝角三角形,AC>AB,∠A是钝角,其他条件不变,试探究AP与AQ的位置关系和数量关系,请画出图形并直接写出结论.    备用图解析　(1)=.提示:设CE、BD交于点F,∵BD、CE是△ABC的高,∴∠BEF=∠CDF=90°,∵∠BFE=∠CFD,∠1=90°-∠CFD,∠2=90°-∠BFE,∴∠1=∠2.(2)结论:AP=AQ,AP⊥AQ.证明:在△QAC和△APB中, ∴△QAC≌△APB(SAS),∴AQ=AP,∠QAC=∠P,∵∠DAP+∠P=90°,∴∠DAP+∠QAC=90°,即∠QAP=90°,∴AP⊥AQ.(3)AP=AQ,AP⊥AQ,如图所示. 提示:∵BD、CE是△ABC的高,∴BD⊥AC,CE⊥AB,∴∠1+∠CAE=90°,∠2+∠DAB=90°,∵∠CAE=∠DAB,∴∠1=∠2.在△QAC和△APB中, ∴△QAC≌△APB(SAS),∴AQ=AP,∠QAC=∠P,∵∠PDA=90°,∴∠P+∠PAD=90°,∴∠QAC+∠PAD=90°,∴∠QAP=90°,∴AP⊥AQ.