青岛版初中八年级数学上册期末素养综合测试(二)课件

这是一份青岛版初中八年级数学上册期末素养综合测试(二)课件，共60页。

一、单选题(本大题共8小题,在每个小题给出的四个选项中, 只有一项是正确的,请把正确的选项选出来,每小题选对得4 分,错选、不选均记0分)1.(2023湖南益阳中考)下列正方体的展开图中,是轴对称图 形的是 (　　)
A B C D
解析　选项A,B,C中的图形都不能找到一条直线,使图形沿 这条直线折叠,直线两旁的部分能够互相重合,所以不是轴对 称图形;D选项中的图形能找到这样一条直线,使图形沿这条 直线折叠,直线两旁的部分能够互相重合,所以是轴对称图 形,故选D.
2.(2024山东泰安肥城期末)已知点A(m-2,1)与点B(5,n-1)关于 y轴对称,则(m+n)2 024的值为 (　　)A.0　    B.1　    C.-1　    D.32 024
解析　因为点A(m-2,1)与点B(5,n-1)关于y轴对称,所以m-2=- 5,n-1=1,解得m=-3,n=2,所以(m+n)2 024=(-3+2)2 024=1.故选B.
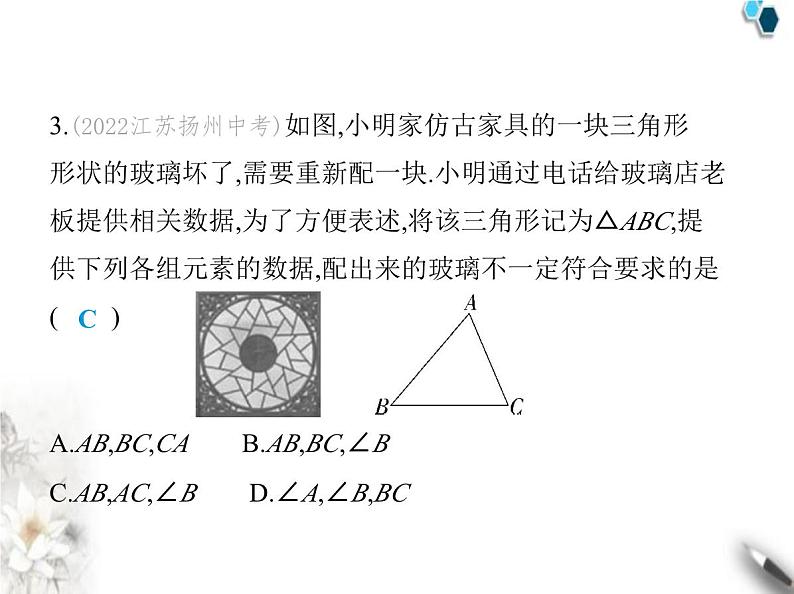
3.(2022江苏扬州中考)如图,小明家仿古家具的一块三角形 形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老 板提供相关数据,为了方便表述,将该三角形记为△ABC,提 供下列各组元素的数据,配出来的玻璃不一定符合要求的是 (　　)A.AB,BC,CA　    B.AB,BC,∠BC.AB,AC,∠B　    D.∠A,∠B,BC
解析　选项A,三角形三边对应相等,两三角形全等,不合题 意;选项B,三角形两边及夹角对应相等,两三角形全等,不合 题意;选项C,三角形两边及一边的对角对应相等,两三角形不 一定全等,符合题意;选项D,三角形两角及一角的对边对应相 等,两三角形全等,不合题意.故选C.
4.(2023河南洛阳伊川期末)下列四个命题:①同位角相等,两 直线平行;②等边三角形的三个内角相等;③全等三角形的对 应角相等;④如果a=b,那么a2=b2.它们的逆命题是真命题的有 (　　)A.1个　    B.2个　    C.3个　    D.4个
解析　①同位角相等,两直线平行的逆命题为两直线平行,同 位角相等,逆命题是真命题;②等边三角形的三个内角都相等 的逆命题为三个内角相等的三角形是等边三角形,逆命题是 真命题;③全等三角形的对应角相等的逆命题为角对应相等 的两个三角形全等,逆命题为假命题;④如果a=b,那么a2=b2的 逆命题为如果a2=b2,那么a=b,逆命题为假命题.综上,逆命题是 真命题的有2个,故选B.
5.(2020浙江衢州中考)过直线l外一点P作直线l的平行线,下 列尺规作图中错误的是 (　　) A B C D
解析　选项A作了角的平分线与等腰三角形,能得到一组内 错角相等,从而可证两直线平行;选项B作了一个角等于已知 角,由同位角相等,可证两直线平行;选项C,在同一平面内,垂 直于同一条直线的两条直线互相平行;选项D,作图只截取了 两条线段相等,无法保证两直线平行.故选D.
6.(2024广西南宁三中期中)如图,在Rt△ABC中,∠ACB=90°, ∠B=60°,CD是△ABC的高,且BD=1,则AD的长为 (　　)A.2.5　    B.3　    C.3.5　    D.4
解析　因为CD是△ABC的高,∠B=60°,所以∠BCD=90°-∠B =30°,所以BC=2BD=2×1=2.在Rt△ABC中,因为∠ACB=90°,∠ B=60°,所以∠A=90°-∠B=30°,所以AB=2BC=2×2=4,所以AD= AB-BD=4-1=3,故选B.
7.小明花整数元网购了一本《趣味数学》,让同学们猜书的 价格.甲说:“至少15元.”乙说“至多13元.”丙说:“至多10 元.”小明说:“你们都猜错了.”那这本书的价格为 (　　)A.12元　    B.13元C.14元　    D.无法确定
解析　由题意可得,甲、乙、丙的说法都是错误的,甲的说法 错误,说明这本书的价格少于15元,乙、丙的说法错误,说明 这本书的价格高于13元,又因为小明花整数元网购了一本 《趣数学》,所以这本书的价格是14元.
8.(新独家原创)如图,△ABC为等腰直角三角形,∠C=90°,将 △ABC按如图所示的方式进行折叠,使点A与BC边上的点F 重合,折痕分别与AC,AB交于点D,E.下列结论:①∠1=∠2;② ∠1+∠2=90°;③∠3+∠B=90°;④DF∥AB.其中一定正确的有 (　　)
A.1个　    B.2个　    C.3个　    D.4个
解析　由折叠的性质可知,∠A=∠3,∠ADE=∠FDE,∠AED= ∠FED.因为△ABC为等腰直角三角形,∠C=90°,所以∠A=∠ B=∠3=45°,所以∠3+∠B=90°,③正确;设∠ADE=∠FDE=α, ∠AED=∠FED=β,所以∠1+∠ADE+∠FDE=∠1+2α=180° ①,∠2+∠AED+∠FED=∠2+2β=180°②,∠A+α+β=180°,所 以α+β=180°-∠A=135°,①+②得∠1+2α+∠2+2β=∠1+∠2+2 (α+β)=360°,所以∠1+∠2=90°,②正确;因为∠1+∠2=90°,∠1 与∠2不一定相等,所以①不一定正确;因为点F在BC边上,不 固定,所以DF与AB不一定平行,④不一定正确.
二、多选题(本大题共4小题,在每个小题给出的四个选项中, 有多项符合题目要求,全部选对得5分,部分选对得2分,错 选、多选、不选均记0分)
9.(2022山东潍坊诸城期末)如图,在探究证明“三角形的内 角和是180°”时,综合实践小组的同学作了如下四种辅助线, 其中能证明“三角形内角和是180°”的是 ( 　　) 图① 图② 图③ 图④
A.如图①,过C作EF∥AB
B.如图②,过AB上一点D作DE∥BC,DF∥ACC.如图③,延长AC到F,过C作CE∥ABD.如图④,过点C作CD⊥AB于点D
解析　选项A,由EF∥AB,得∠ECA=∠A,∠FCB=∠B,由∠E- CA+∠ACB+∠FCB=180°,得∠A+∠ACB+∠B=180°;选项B, 由ED∥BC,得∠EDF=∠BFD,∠ADE=∠B,由DF∥AC,得∠A =∠FDB,∠C=∠BFD,所以∠C=∠EDF,由∠ADE+∠EDF+∠ FDB=180°,得∠B+∠C+∠A=180°;选项C,由CE∥AB,得∠A= ∠FCE,∠B=∠BCE,由∠FCE+∠ECB+∠ACB=180°,得∠A+ ∠B+∠ACB=180°;选项D,由CD⊥AB,得∠ADC=∠CDB=90°, 无法证得三角形内角和是180°.
10.(新独家原创)下列各式中,运算正确的是 (　 　)A. = B. ÷ =- C.若把分式 的x,y同时扩大为原来的3倍,则分式的值扩大为原来的3倍D. - = 
解析　选项A, = = ,错误;选项B, ÷ =- · =- ,正确;选项C,把分式 中的x和y同时扩大为原来的3倍,得 = =3× ,所以分式的值扩大为原来的3倍,正确;选项D, - = - = = = ,正确.故选BCD.
11.(2024山东潍坊昌乐期末)抽查部分用户的用电量,统计数 据如图所示,横轴为用电量(单位:千瓦时),纵轴为户数,关于 这些用户的用电量的描述正确的是 (　　)A.中位数是40 B.平均数是42.6
C.众数是45D.每户的用电量都增加10千瓦时,其方差也会增加10
解析　抽查的用户一共有1+2+2+5+8+2=20(户),这20户居民 用电量的中位数是 =42.5,平均数为 ×(30+35×2+36×2+40×5+45×8+60×2)=42.6,众数是45,每户的用电量都增加10 千瓦时,其平均数增加10,但是方差不变.故选BC.
12.(2023山东潍坊奎文期中)如图,在△ABC中,AB=AC,∠B=36°,分别以点A,C为圆心,大于 AC的长为半径画弧,两弧相交于点D,E,作直线DE分别交AC,BC于点F,G.以G为圆心,GC长 为半径画弧,交BC于点H(除C外),连接AG,AH.下列说法正确 的是( 　　)
A.GA=GC　    B.△BAG≌△CAHC.DE∥AH　    D.∠GAH=3∠BAH
解析　由作法可得GF垂直平分AC,HG=GC,所以GA=GC,选 项A正确.因为AB=AC,所以∠C=∠B=36°.因为GA=GC,所以 ∠GAC=∠C=36°,所以∠AGH=∠GAC+∠C=72°.因为GA= GC=GH,所以∠GAH=∠GHA= ×(180°-72°)=54°,所以∠CAH=90°.因为∠B=36°,∠AGB=72°,所以∠BAG=72°,所以∠ AGB=∠BAG,所以△BAG是顶角为36°的等腰三角形,所以△ BAG与△CAH不全等,选项B错误.因为FG⊥AC,∠CAH=90°, 所以DE∥AH,选项C正确.因为∠GHA=∠B+∠BAH,所以∠
BAH=54°-36°=18°,所以∠GAH=3∠BAH,选项D正确.故选 ACD.
三、填空题(本大题共4小题,共20分,只要求填写最后结果,每 小题填对得5分)
13.(2023山东菏泽定陶期中)已知 = = ≠0,且2a-3b+c≠0,则 的值为　　　    .
14.(2023湖北黄冈部分学校期中)如图,在△ABC中,∠ABC=62°,∠ACB=50°,∠ACD是△ABC的外角,∠ACD和∠ABC的平 分线交于点E,则∠AEB=　　　    °.
解析　如图,过点E作EF⊥BA交BA的延长线于F,EG⊥AC于 G,EH⊥BD于H.因为CE平分∠ACD,EG⊥AC,EH⊥BD,所以EG=EH.
因为BE平分∠ABC,EF⊥BA,EH⊥BD,∠ABC=62°,所以EH=EF,∠ABE=31°,所以EF=EG.因为EF⊥BA,EG⊥AC,所以AE平分∠FAC.因为∠ABC=62°,∠ACB=50°,所以∠FAC=62°+50°=112°,所以∠FAE=56°,所以∠AEB=∠FAE-∠ABE=56°-31°=25°.
15.(2023湖北黄冈部分学校期中)如图,点P是∠AOB内一点, 点P关于直线OA的对称点为C,点P关于直线OB的对称点 为D,连接CD交OA,OB于点M和点N,连接PM,PN.若∠AOB=70°,则∠MPN的大小为　　　    度.
解析　如图,连接OC,OP,OD,因为点P关于直线OA的对称点为C,点P关于直线OB的对称 点为D,所以OC=OP=OD,CM=MP,PN=ND,∠COM=∠POM, ∠POB=∠DOB,所以∠OCP=∠OPC,∠OPD=∠ODP,∠MCP =∠MPC,∠NPD=∠NDP,所以∠OCP-∠MCP=∠OPC-∠
MPC,∠OPD-∠NPD=∠ODP-∠NDP,即∠OCD=∠MPO,∠ OPN=∠ODC.因为∠AOB=70°,即∠AOP+∠POB=70°,所以 ∠COD=140°,所以∠OCD+∠ODC=40°,所以∠MPN=∠MPO +∠NPO=∠OCD+∠ODC=40°.
16.(2023北京海淀建华实验学校期中)如图,边长为a的等边 △ABC中,BF是△ABC的边AC上的中线且BF=b,点D在BF上, 连接AD,在AD的右侧作等边△ADE,连接EF,则△AEF周长的 最小值是　　　    (用含a,b的式子表示).
解析　如图,连接CE并延长,得射线CN,因为△ABC,△ADE都是等边三角形,所以AB=AC=a,AD=AE, ∠BAC=∠DAE=∠ABC=60°,所以∠BAD=∠CAE,所以△BAD≌△CAE(SAS),所以∠ABD=∠ACE.
因为BF是△ABC的中线,所以AF=CF= a,BF⊥AC,所以∠CBD=∠ABD=∠ACE=30°.作点A关于直线CN的对称点M,连接FM交CN于E',可知AE+FE的最小值等于AE'+FE'的值.由点A与点M关于直线CN对称可知CA=CM,E'A=E'M,∠ACM =2∠ACN=60°,所以△ACM是等边三角形,所以AM=AC.
因为AF=CF,所以FM=BF=b,所以△AEF周长的最小值=AF+FE'+AE'=AF+FE'+E'M=AF+ FM= a+b.
四、解答题(本大题共7小题,满分78分.解答应写出文字说 明、证明过程或推演步骤)
17.[答案含评分细则](新独家原创)(9分)(1)解方程: - =2;(2)先化简,再求值: ÷ ,其中x= .
解析　(1)去分母,得2x+9-3(4x-7)=2×3(x-3),解整式方程,得x=3, 2分检验:当x=3时,3(x-3)=0,所以x=3是增根,原分式方程无解. 4分(2)原式= ÷ = ÷ = · = · 
=- · =- , 7分当x= =3时,原式=- =-5. 9分
18.[答案含评分细则](2023山东菏泽巨野期中)(10分)甲、乙 两名队员参加射击训练,成绩被制成下列两个统计图:甲队员射击训练成绩统计图
乙队员射击训练成绩统计图根据以上信息,整理分析数据如下:
(1)写出表格中a,b,c,d的值.(2)分别运用表中的四个统计量,简要分析这两名队员的射击 训练成绩,若选派其中一名参赛,你认为应选哪名队员?说明 你的理由.
解析　(1)甲的平均成绩为 =7(环).乙射击的成绩从小到大重新排列为3,4,6,7,7,8,8,8,9,10,处于 最中间位置的数是7与8,所以乙射击成绩的中位数为 =7.5(环),因为数据8出现的次数最多,所以乙射击成绩的众数为 8环,方差为 ×[(3-7)2+(4-7)2+(6-7)2+2×(7-7)2+3×(8-7)2+(9-7)2+(10-7)2]=4.2(环2),
所以a=7,b=7.5,c=8,d=4.2. 5分(2)从平均成绩看,甲、乙二人的成绩相同,均为7环,从中位数 和众数看,乙的成绩较好,从方差看,甲的成绩比乙的成绩稳 定. 7分综合以上各因素,若选派一名队员参加比赛,可选择乙,因为 乙获得高分的可能性更大. 10分答案不唯一,言之有理即可.
19.[答案含评分细则](2024山东聊城东阿三中月考)(10分)已 知:如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有 BF=AC,FD=CD.求证:(1)△ADC≌△BDF;(2)BE⊥AC.
证明　(1)因为AD为△ABC的高,所以AD⊥BC,所以∠ADB=∠ADC=90°. 3分在Rt△ADC与Rt△BDF中, 所以Rt△ADC≌Rt△BDF(HL). 6分(2)由(1)得△ADC≌△BDF,所以∠EBC=∠DAC. 8分又因为∠DAC+∠ACD=90°,
所以∠EBC+∠ACD=90°,∴∠BEC=90°,
所以BE⊥AC. 10分
20.[答案含评分细则](2023河北秦皇岛青龙月考)(10分)如图, OF是∠MON的平分线,点A在射线OM上,P,Q是直线ON上的 两动点,点Q在点P的右侧,且PQ=OA,作线段OQ的垂直平分 线,分别交直线OF,ON于点B,C,连接AB,PB.(1)如图1,请指出AB与PB的数量关系,并说明理由.(2)如图2,当P,Q两点都在射线ON的反向延长线上时,线段AB, PB是否还存在(1)中的数量关系?若存在,请写出证明过程;若 不存在,请说明理由.
图1 图2
解析　(1)AB=PB.理由如下: 1分如图1,连接BQ.因为BC垂直平分OQ,所以BO=BQ,所以∠BOQ=∠BQO. 3分因为OF平分∠MON,所以∠AOB=∠BOQ,所以∠AOB=∠BQO.又因为OA=PQ,所以△AOB≌△PQB(SAS),所以AB=PB. 5分
图1 图2
(2)存在. 6分证明:如图2,连接BQ.因为BC垂直平分OQ,所以BO=BQ,所以∠BOQ=∠BQO.因为OF平分∠MON,∠BOQ=∠FON,所以∠AOF=∠FON=∠BOQ=∠BQC,所以∠BQP=∠AOB, 8分
又因为OA=PQ,所以△AOB≌△PQB(SAS),所以AB=PB. 10分
21.[答案含评分细则](2022重庆中考B卷)(12分)为保障蔬菜 基地种植用水,需要修建灌溉水渠.(1)计划修建灌溉水渠600米,甲施工队施工5天后,增加施工 人员,每天比原来多修建20米,再施工2天完成任务,求甲施工 队增加人员后每天修建灌溉水渠多少米.(2)因基地面积扩大,现还需修建另一条灌溉水渠1 800米,为 早日完成任务,决定派乙施工队与甲施工队同时开工合作修 建这条水渠,直至完工,甲施工队按(1)中增加人员后的修建 速度进行施工,乙施工队修建360米后,通过技术更新,每天比
原来多修建20%,灌溉水渠完工时,两施工队修建的长度恰好 相同,求乙施工队原来每天修建灌溉水渠多少米.
解析　(1)设甲施工队增加人员后每天修建灌溉水渠x米,则 原来每天修建灌溉水渠(x-20)米,根据题意,得5(x-20)+2x=600, 3分解得x=100.答:甲施工队增加人员后每天修建灌溉水渠100米. 6分(2)设乙施工队原来每天修建灌溉水渠y米,则技术更新后每 天修建灌溉水渠y(1+20%)=1.2y米,根据题意,得 + = , 9分
解分式方程,得y=90,经检验,y=90是原分式方程的解,且符合题意.答:乙施工队原来每天修建灌溉水渠90米. 12分
22.[答案含评分细则](2024山东聊城高唐期末)(12分)如图,在 △ABC中,BD,CD分别是∠ABC,∠ACB的平分线,BP,CP分别 是∠EBC,∠FCB的平分线.(1)当∠ABC=64°,∠ACB=66°时,∠D=　　　    °,∠P=　　     °;(2)若∠A=56°,求∠D,∠P的度数;(3)请你猜想,当∠A的大小变化时,∠D+∠P的值是否变化,请 说明理由.
解析　(1)115°;65°. 4分提示:因为BD,CD分别是∠ABC,∠ACB的平分线,所以∠DBC = ∠ABC=32°,∠DCB= ∠ACB=33°,所以∠D=180°-∠DBC-∠DCB=115°.因为∠ABC=64°,∠ACB=66°,所以∠EBC=180°- ∠ABC=116°,∠BCF=180°-∠ABC=114°.因为BP,CP分别是 ∠EBC,∠FCB的平分线,所以∠CBP= ∠EBC=58°,∠BCP= ∠BCF=57°,所以∠P=180°-∠CBP-∠BCP=65°.(2)在△ABC中,因为∠A+∠ABC+∠ACB=180°,
所以∠ABC+∠ACB=180°-∠A=124°.因为BD,CD分别是∠ABC,∠ACB的平分线,所以∠DBC= ∠ABC,∠DCB= ∠ACB,所以∠D=180°-(∠DBC+∠DCB)=180°- (∠ABC+∠ACB)=180°- ×124°=118°. 6分因为BP,CP分别是∠EBC,∠FCB的平分线,所以∠CBP+∠BCP= ∠CBE+ ∠BCF= (∠CBE+∠BCF)=
 (∠A+∠ACB+∠A+∠ABC)= (180°+∠A),所以∠BPC=180°-(∠CBP+∠BCP)=90°- ∠A=90°-28°=62°. 8分(3)∠D+∠P的值不变.理由: 9分因为由(2)知∠D=90°+ ∠A,∠P=90°- ∠A,所以∠D+∠P=180°,所以当∠A的大小变化时,∠D+∠P的值不变. 12分
23.[答案含评分细则](2023浙江杭州余杭期中)(15分)如图,点 O是等边△ABC内一点,∠AOB=100°,∠BOC=α.以OC为边作 等边△OCD,连接AD.(1)求证:△BOC≌△ADC.(2)当α=150°时,试判断△AOD的形状,并说明理由.(3)当α为多少度时,△AOD是等腰三角形?
解析　(1)证明:因为△ABC和△ODC是等边三角形,所以BC= AC,CO=CD,∠ACB=∠DCO=60°,所以∠ACB-∠ACO=∠ DCO-∠ACO,即∠BCO=∠ACD.在△BOC和△ADC中,  所以△BOC≌△ADC(SAS). 4分(2)△AOD是直角三角形. 5分理由:因为△BOC≌△ADC,所以∠BOC=∠ADC.
因为∠BOC=α=150°,∠ODC=60°,所以∠ADO=150°-60°=90°,所以△AOD是直角三角形. 8分(3)易得∠COB=∠CDA=α,∠ADO=α-60°,∠AOD=360°-100°- α-60°=200°-α,因为∠ADO+∠DAC=∠DOC+∠ACO,所以∠DAC=∠DOC+∠ACO-∠ADO=60°+∠ACO-(α-60°)=120°-α+∠ACO.
因为∠OAC=180°-∠AOC-∠ACO=180°-(360°-100°-α)-∠A- CO=α-80°-∠ACO,所以∠OAC+∠DAC=40°,即∠OAD=40°. 10分△AOD是等腰三角形,分三种情况:①若AO=AD,则∠AOD=∠ADO,所以200°-α=α-60°,解得α=130°;②若OA=OD,则∠OAD=∠ADO,所以α-60°=40°,解得α=100°;