初中数学青岛版八年级上册2.1 图形的轴对称多媒体教学ppt课件

这是一份初中数学青岛版八年级上册2.1 图形的轴对称多媒体教学ppt课件，共25页。
知识点1　轴对称与两个图形关于某条直线成轴对称
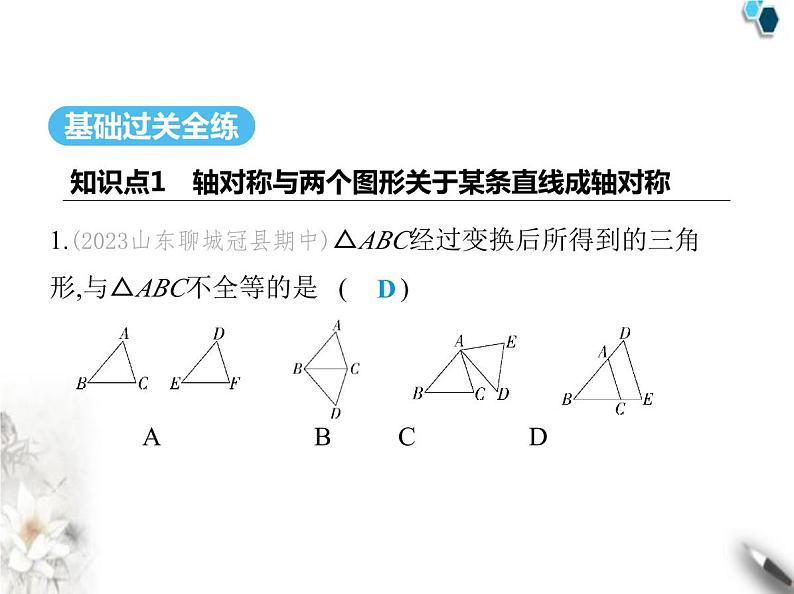
1.(2023山东聊城冠县期中)△ABC经过变换后所得到的三角 形,与△ABC不全等的是 (　　) A 　     B   C　 D
解析　因为平移、旋转、翻折(即轴对称)前、后的两个三 角形全等,所以选项A、B、C不符合题意,故选D.
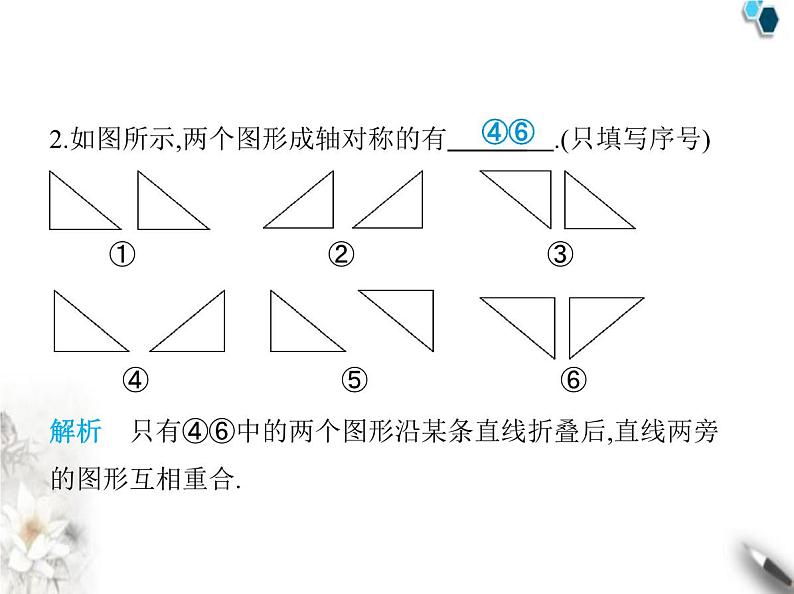
2.如图所示,两个图形成轴对称的有　　　    .(只填写序号)  ① ② ③ ④ ⑤ ⑥
解析　只有④⑥中的两个图形沿某条直线折叠后,直线两旁 的图形互相重合.
知识点2　成轴对称的两个图形的性质
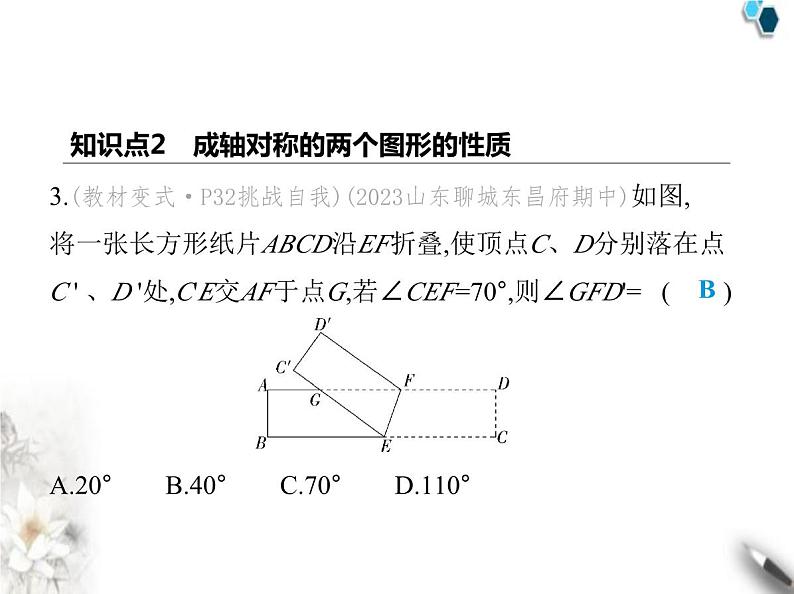
3.(教材变式·P32挑战自我)(2023山东聊城东昌府期中)如图, 将一张长方形纸片ABCD沿EF折叠,使顶点C、D分别落在点 C ' 、D '处,C'E交AF于点G,若∠CEF=70°,则∠GFD'= (　　)A.20°　    B.40°　    C.70°　    D.110°
解析　因为四边形ABCD是长方形,所以AD∥BC,所以∠AFE =∠CEF=70°,所以∠EFD=180°-∠AFE=110°.由折叠,得∠ DFE=∠D'FE=110°,所以∠GFD'=∠D'FE-∠AFE=40°,故选B.
4.(教材变式·P33T4)(2023江苏宿迁沭阳期中)如图,已知△ ABC和△ADC关于直线AC成轴对称,∠B=30°,∠BAD=46°,则 ∠BCD的度数为 (　　)A.120°　    B.116°　    C.106°　    D.96°
解析　因为△ABC和△ADC关于直线AC成轴对称,所以△ABC≌△ADC,所以∠BCA=∠DCA,∠BAC=∠DAC,因为∠BAD=∠BAC+∠DAC=46°,所以∠BAC=∠DAC=23°,所以∠BCA=180°-∠B-∠BAC=127°,所以∠DCA=127°,所以∠BCD=360°-∠BCA-∠DCA=106°.
5.(新独家原创)下列语句:①两个图形关于某条直线成轴对 称,对称点一定在该直线的两旁;②若两个三角形全等,则它 们必是关于某条直线成轴对称的图形;③成轴对称的两个图 形一定全等;④成轴对称的是一个图形;⑤如果△ABC与△ DEF成轴对称,那么它们的周长一定相等.其中正确的是　     .(只填序号)
解析　根据成轴对称的两个图形的性质可知,成轴对称的两 个图形一定全等,周长一定相等,但两个三角形全等,它们未 必是关于某条直线成轴对称的图形.两个图形关于某条直线 成轴对称,对称点可能在该直线的两旁,也可能在该直线(对 称轴)上,所以③⑤正确,①②④错误.
6.(2024北京人大附中朝阳学校期中)如图,三角形纸片ABC 中,AB=AC,将其折叠,使点A与点B重合,折痕为ED,点E,D分别 在AB,AC上,若AB=6,BC=4,那么△BDC的周长为　　　    .
解析　由折叠得BD=AD,所以△BDC的周长=BD+CD+BC= AD+CD+BC=AC+BC.因为AB=AC=6,BC=4,所以AC+BC=6+4 =10,所以△BDC的周长为10.
7.如图,两个四边形关于直线l成轴对称,∠C=90°,试写出 AB、HE的长度,并求出∠G的度数.
解析　因为两个四边形关于直线l成轴对称,所以四边形ABCD≌四边形FEHG,所以∠H=∠C=90°,∠F=∠A=80°,AB=EF=5 cm,HE=BC=4 cm,所以∠G=360°-∠H-∠E-∠F=360°-90°-135°-80°=55°.
8.如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D 落在点G处.(1)求证:△FGC≌△EBC.(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
解析　 (1)证明:因为四边形ABCD是长方形,所以AD=BC,∠A=∠D=∠B=∠DCB=90°.根据折叠的性质得GC=AD,∠G=∠D=∠GCE=∠A=90°,所以 GC=BC,∠G=∠B.因为∠GCF+∠ECF=90°,∠BCE+∠ECF=90°,所以∠GCF=∠BCE.所以△FGC≌△EBC(ASA).(2)由折叠的性质知S四边形ECGF=S四边形EADF,由(1)得△FGC≌△E-
BC,所以S△FGC=S△EBC,所以S四边形ECGF=S四边形EBCF,所以S四边形EADF=S四边形 EBCF= S长方形ABCD.因为AB=8,AD=4,所以S长方形ABCD=8×4=32,所以S四边形ECGF= ×32=16.
9.(方程思想)(2023北京昌平期末,5,★★☆)在Rt△ABC中,∠ C=90°,AC=8,BC=6,AB=10.现将△ABC按如图所示的方式折 叠,使点C落在AB上的点D处,折痕为BE,则DE的长为 (　　)A.3　    B.4　    C.6　    D.5
解析　因为∠C=90°,所以BC⊥AE,由折叠得△BCE≌△ BDE,所以DE=CE,∠BDE=∠C=90°,所以DE⊥AB,因为S△ABE=  AB·DE= AE·BC,且AE=AC-CE=8-CE=8-DE,所以 ×10×DE= ×(8-DE)×6,解得DE=3,故选A.
10.(2024山东潍坊青州期中,14,★★☆)如图,将一张长方形 纸片ABCD沿对角线BD折叠后,点C落在点E处,BE交AD于点 F,再将△DEF沿DF折叠后,点E落在点G处,若DG刚好平分∠ ADB,则∠EDF的度数为　　　    .
解析　设∠EDF=α,由折叠的性质,得∠ADG=∠EDF=α,∠ BDC=∠BDE.因为DG平分∠ADB,所以∠ADG=∠BDG=α,所 以∠ADB=∠ADG+∠BDG=2α,∠BDE=∠EDF+∠ADG+∠ BDG=3α,所以∠BDC=∠BDE=3α,所以∠ADC=∠ADB+∠ BDC=2α+3α=5α.因为四边形ABCD为长方形,所以∠ADC=90 °,所以5α=90°,解得α=18°,即∠EDF=18°.
11.(2021湖南湘西州中考,17,★★☆)如图,将一条对边互相 平行的纸带进行两次折叠,折痕分别为AB、CD,若CD∥BE, ∠1=20°,则∠2的度数是　　　    .
解析　如图,分别延长MA、EB、DB,∵AC∥DG,∴∠1=∠4=20°,由折叠,得∠3=∠1=20°,∵MN∥ EB,∴∠3=∠5=20°,∴∠EBG=∠4+∠5=40°,∵CD∥BE,∴∠ 2=∠EBG=40°.
12.(运算能力)(2024山东潍坊昌乐期中)如图1,将长方形 ABEF的一角向长方形内部折叠,使角的顶点A落在点A'处, OC为折痕,则OC平分∠AOA'.(1)若∠AOC=25°,求∠A'OB的度数.(2)若点D在线段BE上,将顶点B沿着折痕OD折叠,落在点B' 处,且点B'在长方形内.①如果点B'刚好在线段A'O上,如图2所示,求∠COD的度数.②如果点B'不在线段A'O上,且∠A'OB'=40°,求∠AOC+∠BOD的度数.
解析　(1)因为OC平分∠AOA',∠AOC=25°,所以∠A'OA=2∠ AOC=50°,所以∠A'OB=180°-∠A'OA=180°-50°=130°.(2)①由折叠的性质可知,∠COA'= ∠AOA',∠DOB'= ∠BOA',因为∠AOA'+∠BOA'=180°,所以∠COD=∠COA'+∠ DOB'= (∠AOA'+∠BOA')= ×180°=90°.②分情况讨论:a.当点B'在∠AOA'外时,如图1,因为∠A'OB'=4 0°,所以∠AOA'+∠BOB'=180°-40°=140°,因为∠COA= ∠
AOA',∠DOB= ∠BOB',所以∠AOC+∠BOD= (∠AOA'+∠BOB')= ×140°=70°;b.当点B'在∠AOA'内时,如图2,因为∠A'OB'=40°,所以∠AOA' +∠BOB'=180°+∠A'OB'=220°,因为∠COA= ∠AOA',∠DOB= ∠BOB',所以∠AOC+∠BOD= (∠AOA'+∠BOB')= ×220°=110°.综上所述,∠AOC+∠BOD的度数为70°或110°.