青岛版八年级上册2.4 线段的垂直平分线课文内容课件ppt

这是一份青岛版八年级上册2.4 线段的垂直平分线课文内容课件ppt，共27页。

知识点1　垂直平分线的定义与性质
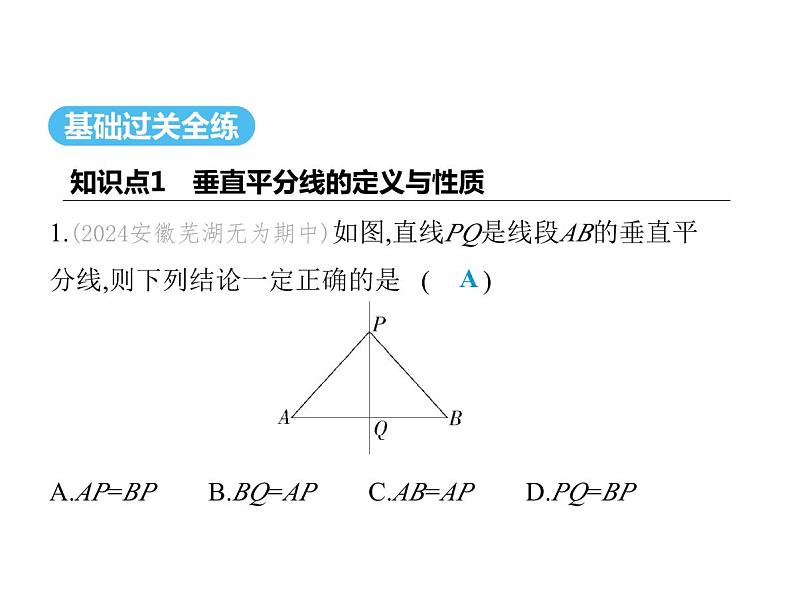
1.(2024安徽芜湖无为期中)如图,直线PQ是线段AB的垂直平 分线,则下列结论一定正确的是 (　　) A.AP=BP　    B.BQ=AP C.AB=AP　    D.PQ=BP
解析　因为直线PQ是线段AB的垂直平分线,所以AP=BP,选 项A正确,故选A.
2.(2024山东聊城莘县期中)如图,在△ABC中,AB的垂直平分 线交AB于点D,交BC于点E,连接AE.若BC=5,AC=4,则△ACE 的周长为 (　　)A.9　    B.10　    C.13　    D.14
解析　因为直线DE是线段AB的垂直平分线,所以EA=EB,所 以△ACE的周长=EA+EC+AC=EB+EC+AC=BC+AC=9,故选 A.
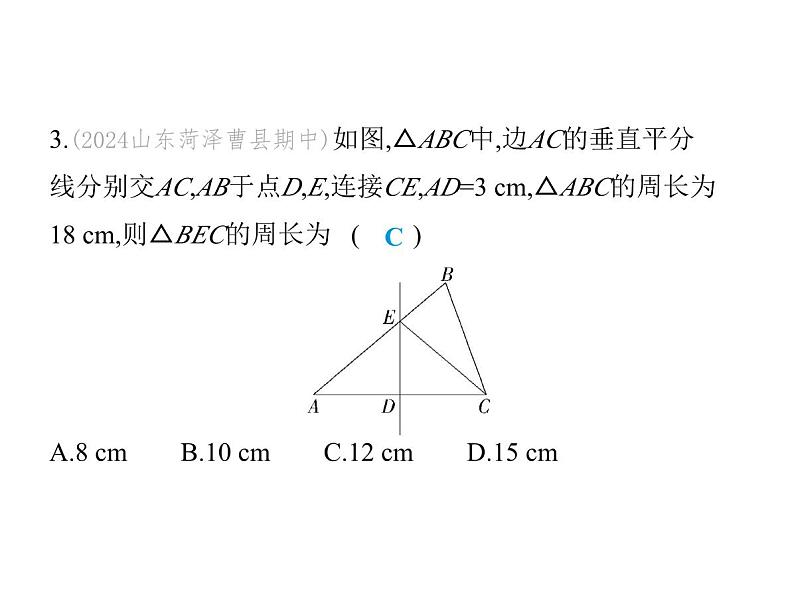
3.(2024山东菏泽曹县期中)如图,△ABC中,边AC的垂直平分 线分别交AC,AB于点D,E,连接CE,AD=3 cm,△ABC的周长为 18 cm,则△BEC的周长为 (　　) A.8 cm　    B.10 cm　    C.12 cm　    D.15 cm
解析　因为边AC的垂直平分线分别交AC,AB于点D,E,所以 AE=CE,AD=CD= AC,因为AD=3 cm,所以AC=6 cm.因为△ABC的周长=AB+BC+AC=18 cm,所以AB+BC=12 cm,所以△ BEC的周长为BE+CE+BC=BE+AE+BC=AB+BC=12 cm,故选 C.
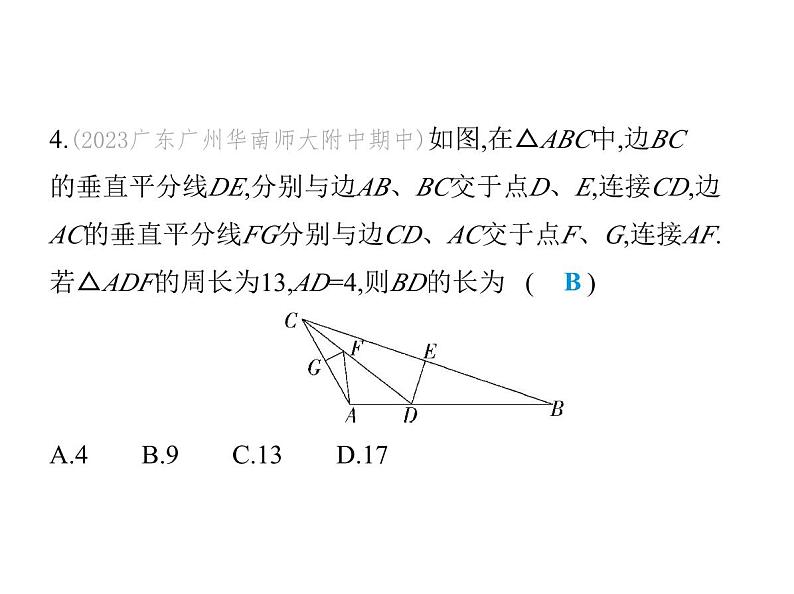
4.(2023广东广州华南师大附中期中)如图,在△ABC中,边BC 的垂直平分线DE,分别与边AB、BC交于点D、E,连接CD,边 AC的垂直平分线FG分别与边CD、AC交于点F、G,连接AF. 若△ADF的周长为13,AD=4,则BD的长为 (　　)A.4　    B.9　    C.13　    D.17
解析　因为FG垂直平分AC,所以CF=AF,所以△ADF的周长 =AF+DF+AD=CF+DF+AD=CD+AD=13,因为AD=4,所以CD= 9,因为DE垂直平分BC,所以BD=CD=9,故选B.
5.(2024北京二中教育集团期中)如图,在△ABC中,AB的垂直 平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则 BC的长为　　　    .
解析　因为直线DE是线段AB的垂直平分线,所以EB=AE=4, 所以BC=BE+EC=4+2=6.
6.(新独家原创)如图,在△ABC中,点E在AB的垂直平分线上, 且ED=CD,AD⊥BC.若AC=3,ED=1,则BD=　　　    .
解析　因为AD⊥BC,ED=CD,所以直线AD是线段EC的垂直 平分线,所以AE=AC=3.因为点E在AB的垂直平分线上,所以 BE=AE=3,所以BD=BE+ED=3+1=4.
7.如图,直线PD和直线PE分别是线段AB,BC的垂直平分线,判 断PA和PC的数量关系,并说明理由. 
解析    PA=PC.理由如下:如图,连接PB,因为直线PD是线段AB的垂直平分线,所以PA= PB,同理PC=PB,所以PA=PC.
知识点2　垂直平分线的判定
8.(2024海南海口海南中学期中)如图,AC=AD,BC=BD,则有 (　　)A.CD平分∠ACB B.CD垂直平分ABC.AB与CD互相平分 D.AB垂直平分CD
解析　因为AC=AD,所以点A在CD的垂直平分线上,因为BC= BD,所以点B在CD的垂直平分线上,所以AB垂直平分CD,故 选D.
9.(2024山东聊城临清期中改编)如图,A、B、C三个居民小区 的位置成三角形,现决定在三个小区之间修建一个购物超市, 使超市到三个小区的距离相等,则超市应建在 (　　)A.在AC,BC两边上的高线的交点处B.在AC,BC两边上的中线的交点处C.在AC,BC两边垂直平分线的交点处D.在AC边上的高线与BC边上的中线的交点处
解析　超市到B、C小区的距离相等,根据垂直平分线的判定 方法,超市应该在线段BC的垂直平分线上,同理,超市应该在 线段AC的垂直平分线上,所以超市应建在这两条垂直平分线 的交点处.
10.(2023山东菏泽单县期中)如图,AD与BC相交于点O,连接 AB、CD并延长,相交于点E,连接OE、BD,OA=OC,∠A=∠C, BE=DE.试说明:OE垂直平分BD.
解析　在△AOB与△COD中, 所以△AOB≌△COD(ASA),所以OB=OD,所以点O在线段BD的垂直平分线上,因为BE=DE,所以点E在线段BD的垂直平分线上,所以OE垂 直平分BD.
11.(2023浙江湖州长兴月考,10,★★☆)如图,在△ABC中,BD 是△ABC的中线,EF垂直平分BC,且BD与EF相交于点G,连接 AG,CG,若四边形CDGE与四边形ACEG的面积分别为7和11, 则△ABC的面积为 (　　)A.18　    B.20　    C.22　    D.36
解析　因为四边形CDGE与四边形ACEG的面积分别为7和1 1,所以S△AGD=11-7=4,因为BD是△ABC的中线,所以S△ABD=S△BDC,S△CGD=S△AGD=4,所以 S△CGE=3.因为直线EF是边BC的垂直平分线,所以E是BC的中点,所以S△BEG=S△CGE=3,所以S△BDC=S△BEG+S△CGE+S△CGD=3+3+4=10,所以S△ABC=S△ABD+S△BDC=2S△BDC=20,故选B.
12.(2024山东菏泽单县期中,21,★★☆)如图,△ABC中,∠ ACB=90°,AE平分∠BAC,DE⊥AB于D.(1)若∠BAC=48°,求∠DEA的度数.(2)求证:直线AE是线段CD的垂直平分线.
解析　(1)因为∠BAC=48°,AE平分∠BAC,所以∠EAD= ∠BAC=24°.因为DE⊥AB,所以∠ADE=90°,所以∠DEA=90°-∠EAD=66°.(2)证明:因为DE⊥AB,所以∠ADE=∠ACB=90°.又因为AE平分∠BAC,所以∠DAE=∠CAE.
在△ADE和△ACE中, 所以△ADE≌△ACE(AAS),所以AD=AC,ED=EC,所以点A在线段CD的垂直平分线上,点E在线段CD的垂直平 分线上,所以直线AE是线段CD的垂直平分线.
13.(2023黑龙江牡丹江期中,23,★★☆)如图,在△ABC中,边 AB、AC的垂直平分线分别交BC于点D、E,连接AD、AE.(1)若BC=10,求△ADE的周长.(2)设直线DM、EN交于点O.①试判断点O是否在BC的垂直平分线上,并说明理由.②若∠BAC=100°,求∠BOC的度数.
解析　(1)因为AB、AC的垂直平分线分别交BC于点D、E,所 以AD=BD,AE=CE,所以AD+DE+AE=BD+DE+CE=BC=10,即△ADE的周长为10.(2)①点O在BC的垂直平分线上,理由如下:如图,连接AO、BO、CO,因为直线DM、EN分别是线段AB、AC的垂直平分线,所以OB=OA,OA=OC,所以OB=OC,
所以点O在BC的垂直平分线上. ②因为OM⊥AB,ON⊥AC,所以∠AMO=∠ANO=90°,在四边形AMON中,因为∠MAN=100°,∠AMO+∠ANO+∠MAN+∠MON=360°,所