初中青岛版第5章 几何证明初步5.6 几何证明举例教案配套ppt课件

这是一份初中青岛版第5章 几何证明初步5.6 几何证明举例教案配套ppt课件，共31页。
知识点7　直角三角形全等的判定定理“HL”
1.(2024山东泰安泰山期末)如图,BE=CF,AE⊥BC,DF⊥BC,要 根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条 件是 (　　)A.AE=DF　    B.∠A=∠DC.∠B=∠C　    D.AB=DC
解析　因为AE⊥BC,DF⊥BC,所以∠CFD=∠AEB=90°,在Rt △ABE和Rt△DCF中,已知直角边BE=CF,若用“HL”证两 三角形全等,需添加条件AB=CD.故选D.
2.(2024河北衡水故城期末)下列说法不正确的是 (　　)A.两条直角边对应相等的两个直角三角形全等B.一锐角和斜边对应相等的两个直角三角形全等C.斜边和一直角边对应相等的两个直角三角形全等D.有两边相等的两个直角三角形全等
解析　两条直角边对应相等的两个直角三角形全等,可根据 “SAS”来判断,选项A不符合题意;一锐角和斜边对应相等 的两个直角三角形全等,可根据“AAS”来判断,选项B不符 合题意;斜边和一直角边对应相等的两个直角三角形全等,可 根据“HL”来判断,选项C不符合题意;如果第一个直角三角 形的两条直角边长分别为3,4,第二个直角三角形一条直角边 长为3,斜边长为4,那么这两个直角三角形不全等,选项D错 误,符合题意,故选D.
3.(2024山东菏泽成武期中)如图,BE,CD是△ABC的高,且BD= EC,判定△BCD≌△CBE的依据是“　　　　　　    ”.
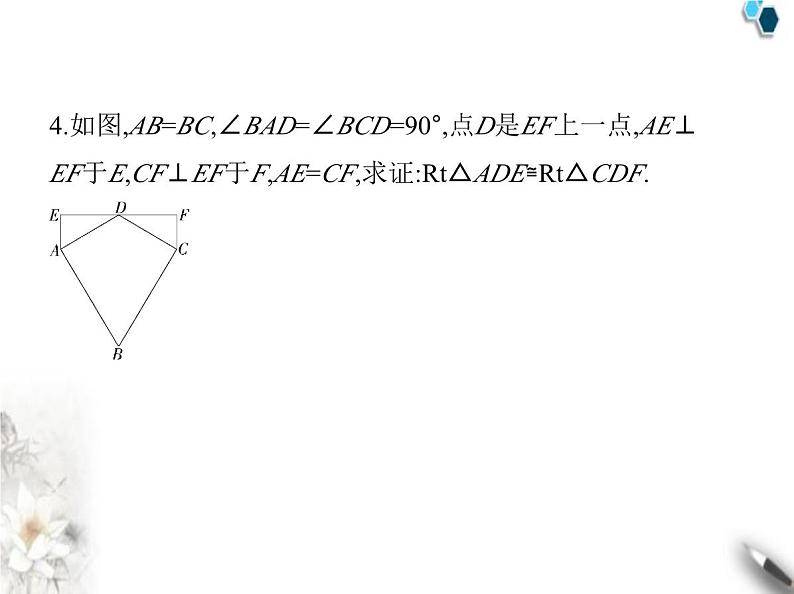
4.如图,AB=BC,∠BAD=∠BCD=90°,点D是EF上一点,AE⊥ EF于E,CF⊥EF于F,AE=CF,求证:Rt△ADE≌Rt△CDF.
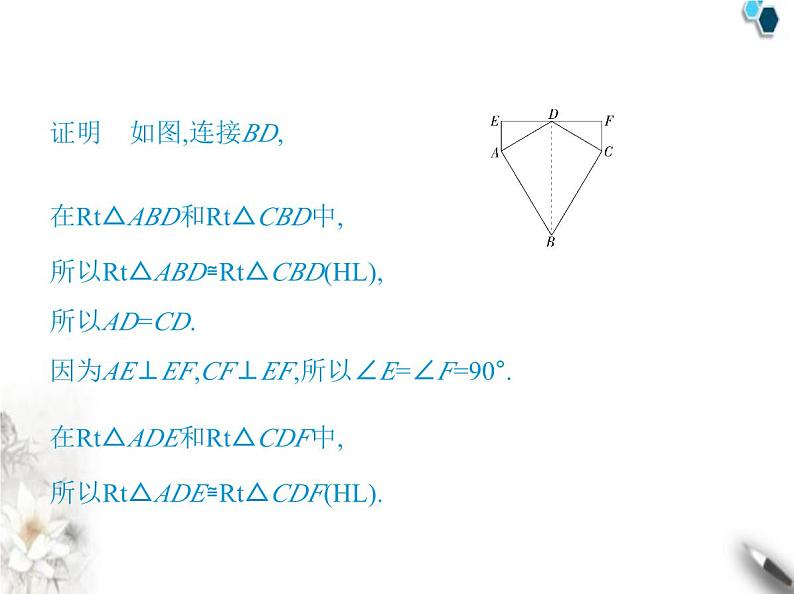
证明　如图,连接BD,
在Rt△ABD和Rt△CBD中, 所以Rt△ABD≌Rt△CBD(HL),所以AD=CD.因为AE⊥EF,CF⊥EF,所以∠E=∠F=90°.在Rt△ADE和Rt△CDF中, 所以Rt△ADE≌Rt△CDF(HL).
5.(方程思想)(新独家原创)如图,AD是△ABC的角平分线,DF ⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,求△EDF的面积.
解析　如图,过点D作DH⊥AC于H,因为AD是△ABC的角平分线,DF⊥AB,所以DF=DH.在Rt△DEF和Rt△DGH中, 
所以Rt△DEF≌Rt△DGH(HL),所以S△EDF=S△GDH.同理Rt△ADF≌Rt△ADH,所以S△ADF=S△ADH.设S△EDF=S△GDH=S,所以38+S=50-S,解得S=6,即△EDF的面积是6.
6.(2022山东聊城茌平期末)已知∠A=∠D=90°,AB=DC,点E,F 在直线BC上,位置如图所示,且BE=CF.(1)求证:AF=DE;(2)若PO平分∠EPF,求证:PO垂直平分线段BC.
证明　(1)∵BE=CF,∴BE+BC=CF+BC,∴CE=BF.在Rt△ABF与Rt△DCE中, ∴Rt△ABF≌Rt△DCE(HL),∴AF=DE.(2)∵Rt△ABF≌Rt△DCE,∴∠E=∠F,∴PE=PF,又∵PO平分∠EPF,∴PO⊥BC,EO=FO.又∵EB=FC,∴BO=CO,∴PO垂直平分线段BC.
7.(2024北京二中教育集团期中,8,★★☆)如图,BN为∠MBC 的平分线,P为BN上一点,且PD⊥BC于点D,∠APC+∠ABC=1 80°,给出下列结论:①∠MAP=∠BCP;②PA=PC;③AB+BC=2 BD;④四边形BAPC的面积是△PBD面积的2倍.其中正确的 结论有 (　　)
A.4个　    B.3个　    C.2个　    D.1个
解析　如图,过点P作PK⊥AB,垂足为点K.因为PK⊥AB,PD⊥ BC,BN为∠MBC的平分线,所以PK=PD.在Rt△BPK和Rt△ BPD中, 所以Rt△BPK≌Rt△BPD(HL),所以BK=BD.因为∠APC+∠ABC=180°,∠ABC+∠KPD=180°,所以∠ KPD=∠APC,所以∠APD+∠APK=∠APD+∠CPD,所以∠ APK=∠CPD,所以∠MAP=∠BCP,故①正确;在△PAK和△ PCD中, 所以△PAK≌△PCD(ASA),所以AK=
CD,PA=PC,所以BK-AB=BC-BD,所以BD-AB=BC-BD,所以AB +BC=2BD,故②③正确;因为Rt△BPK≌Rt△BPD,△PAK≌△ PCD,所以S△BPK=S△BPD,S△APK=S△PDC,所以S四边形ABCP=S四边形KBDP=2S△PBD,故④正确.故选A.
8.(2023山东聊城东昌府期中,12,★★☆)已知:如图,BD为△ ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA, 过E作EF⊥AB,垂足为F.下列结论:①△ABD≌△EBC;②∠ BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确 的是 (　　)
A.①②③　    B.①③④ C.①②④　    D.①②③④
解析　因为BD为△ABC的角平分线,所以∠ABD=∠CBD.在 △ABD和△EBC中, 所以△ABD≌△EBC(SAS),故①正确;因为BD=BC,BE=BA,所以∠BDC=∠BCD,∠ BEA=∠BAE.因为∠ABE=∠CBE,所以∠BCD=∠BDC=∠ BAE=∠BEA.因为△ABD≌△EBC,所以∠BCE=∠BDA,所以 ∠BCE+∠BCD=∠BDA+∠BDC=180°,故②正确;因为∠BCE =∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠
BCD=∠BEA,所以∠DCE=∠DAE,所以△ACE为等腰三角形, AE=EC.因为△ABD≌△EBC,所以AD=EC,所以AD=AE=EC, 故③正确;过E作EG⊥BC,交BC的延长线于点G,如图,因为E 是BD延长线上的点,EF⊥AB,且BD为△ABC的角平分线,所 以EF=EG,在Rt△BEG和Rt△BEF中, 所以Rt△BEG≌Rt△BEF(HL),所以BG=BF.在Rt△CEG和Rt△AEF 中,  所以Rt△CEG≌Rt△AEF(HL),所以AF=CG,所以
BA+BC=BF+FA+BG-CG=BF+BG=2BF,故④正确.  
9.(2024北京二中教育集团期中,23,★★☆)如图,在△ABC中, BD平分∠ABC,E是BD上一点,EA⊥AB,且EB=EC.(1)如果∠ABC=40°,求∠DEC的度数;(2)求证:BC=2AB.
解析　(1)因为BD平分∠ABC,所以∠EBC= ∠ABC=20°.因为EB=EC,所以∠ECB=∠EBC=20°.因为∠DEC是△EBC的一个外角,所以∠DEC=∠ECB+∠EBC=40°.(2)证明:如图,过点E作EF⊥BC于点F,因为BD平分∠ABC,EA⊥AB,所以EA=EF.在Rt△AEB和Rt△FEB中, 
所以Rt△AEB≌Rt△FEB(HL),所以AB=FB(全等三角形的对应边相等).因为EB=EC,EF⊥BC,所以BC=2FB,所以BC=2AB.
10.(推理能力)(2022山东潍坊潍城期末)已知△ABC是等边三 角形,点D在边BC上.【问题解决】如图1,以AD为一边作等边三角形ADE,连接 BE,求证:BE+BD=AB;【迁移运用】如图2,点F是AB边上一点,以DF为一边作等边 三角形DEF,连接BE,求证:BE+BD=BF;
【类比探究】如图3,点F是AB延长线上一点,以DF为一边作 等边三角形DEF,连接BE,试探究BE,BD,BF三条线段之间存 在怎样的数量关系,请写出你的结论并说明理由.
图1 图2 图3
解析　【问题解决】证明:∵△ABC和△ADE是等边三角形,∴AB=AC=BC,AE=AD,∠DAE=∠BAC=60°,∴∠DAE-∠BAD=∠BAC-∠BAD,即∠BAE=∠CAD.∴△BAE≌△CAD(SAS),∴BE=CD,∴BD+BE=BD+CD=BC.∵AB=BC,∴BE+BD=AB.【迁移运用】证明:如图1,过点D作DG∥AC,交AB于点G,
图1∵△ABC是等边三角形,∴∠ABC=∠A=∠C=60°.∵DG∥AC,∴∠BGD=∠A=60°,∠BDG=∠C=60°.又∵∠ABC=60°,∴△BDG为等边三角形,∴BD=DG=BG.
∵△DEF为等边三角形,∴DE=DF,∠EDF=60°.∵∠BDE=∠BDG-∠EDG=60°-∠EDG,∠FDG=∠EDF-∠EDG=60°-∠EDG,∴∠BDE=∠FDG.在△BDE与△GDF中, ∴△BDE≌△GDF(SAS),∴BE=GF,∴BE+BD=GF+BG=BF.
【类比探究】BD+BF=BE,理由如下:如图2,过点D作DG∥AC,交AB于点G,图2∵△ABC是等边三角形,∴∠ABC=∠A=∠C=60°.
∵DG∥AC,∴∠BGD=∠A=60°,∠BDG=∠C=60°,又∵∠ABC=60°,∴△BDG为等边三角形,∴BD=DG=BG.∵△DEF为等边三角形,∴DE=DF,∠FDE=60°.