初中数学北师大版八年级上册3 勾股定理的应用集体备课ppt课件

这是一份初中数学北师大版八年级上册3 勾股定理的应用集体备课ppt课件，共25页。PPT课件主要包含了学习目标，知识回顾，新知探索，归纳总结，立体图形，平面图形，立体图形上的最短路程，直角三角形模型，台阶问题，做一做等内容，欢迎下载使用。
1. 学会运用勾股定理求立体图形中 两点之间的最短距离（重点）.
2.能够运用勾股定理及其逆定理 解决简单的实际问题（重难点）.
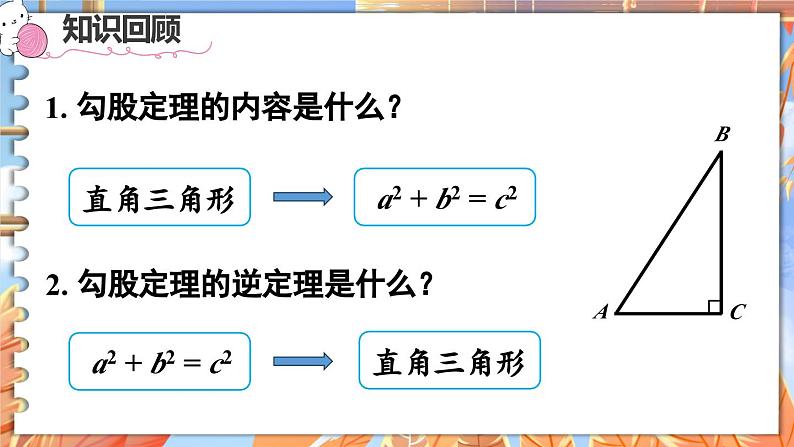
1. 勾股定理的内容是什么？
2. 勾股定理的逆定理是什么？
如图所示，有一个圆柱，它的高等于 12 cm，底面上圆的周长等于 18 cm. 在圆柱下底面的点 A 有一只蚂蚁，它想吃到上底面上与点 A 相对的点 B 处的食物，沿圆柱侧面爬行的最短路程是多少？
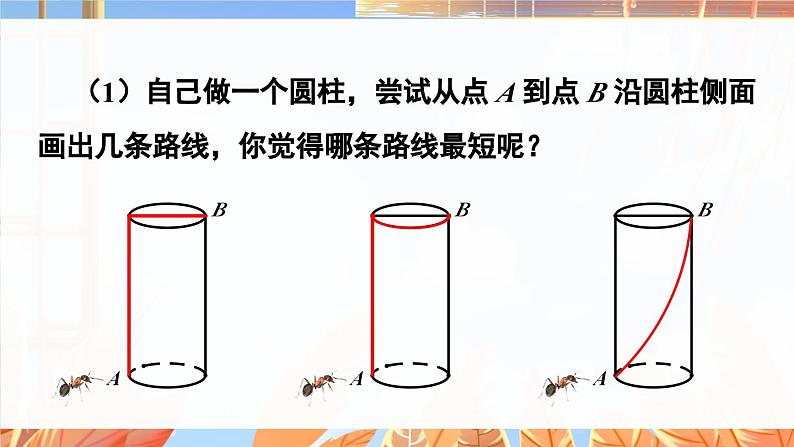
（1）自己做一个圆柱，尝试从点 A 到点 B 沿圆柱侧面画出几条路线，你觉得哪条路线最短呢？
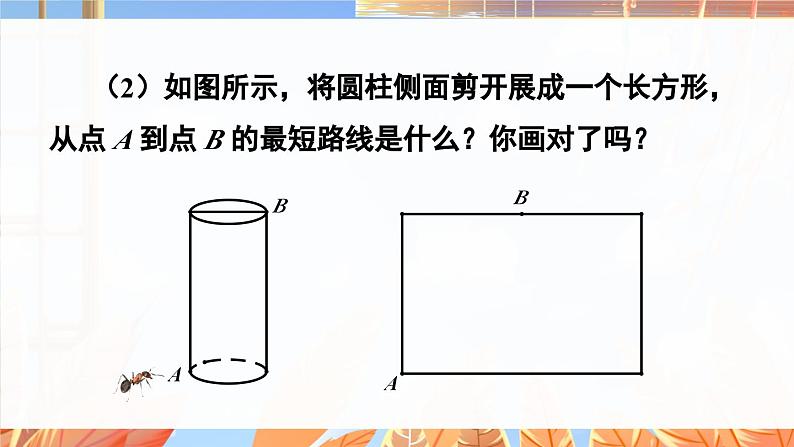
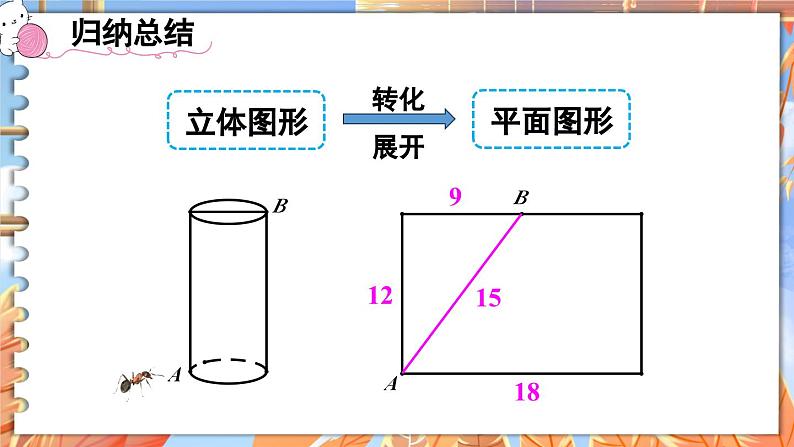
（2）如图所示，将圆柱侧面剪开展成一个长方形，从点 A 到点 B 的最短路线是什么？你画对了吗？
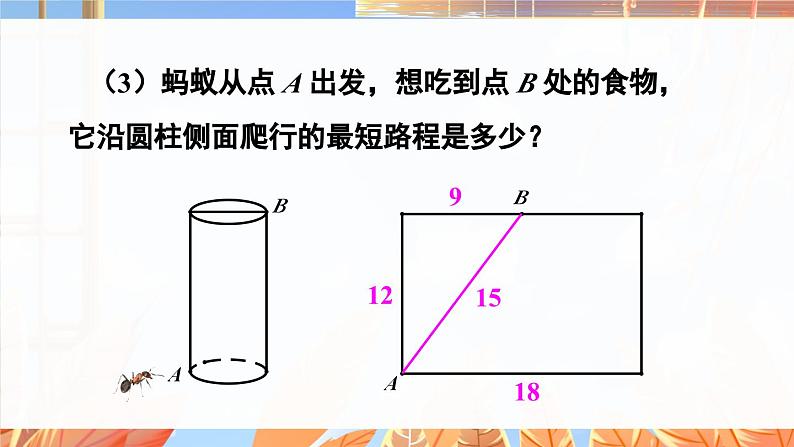
（3）蚂蚁从点 A 出发，想吃到点 B 处的食物，它沿圆柱侧面爬行的最短路程是多少？
（1）先将立体图形的表面展开；（立体→平面）
（2）再作两点之间的连线；（构造直角三角形）
（3）运用勾股定理求出两点之间的距离.
2. 棱柱（以长方体为例）
李叔叔想要检测雕塑（如图）底座正面的边 AD 和边 BC 是否分别垂直于底边 AB，但他随身只带了卷尺. （1）你能替他想办法完成任务吗？
解：利用勾股定理的逆定理，分别量出AB、BC、AC 的长.
如果AB2 + BC2 = AC2，
可得AD和BC分别垂直于底边AB.
（2）李叔叔量得边 AD 长是 30 cm，边 AB 长是 40 cm，点 B，D 之间的距离是 50 cm. 边 AD 垂直于边 AB 吗？
解：因为AD2 + AB2 = 302 + 402 = 502 = BD2，
所以△ABD是直角三角形，所以∠DAB = 90°，即 AD 边垂直于 AB 边.
（3）小明随身只有一个长度为 20 cm 的刻度尺，他能有办法检验边 AD 是否垂直于边 AB 吗？边 BC 与边 AB 呢？
解：在 AD 上取点 M，使 AM = 9 cm，在 AB 上取点 N 使 AN = 12 cm，测量 MN 是否为 15 cm，若是，就垂直；若不是，就不垂直.
下图是一个滑梯示意图，若将滑道 AC 水平放置，则刚好与 AB 一样长. 已知滑梯的高度 CE = 3 m，CD = 1 m，试求滑道 AC 的长.
解：设滑道 AC 的长度为 x m，则 AB 的长度为 x m，AE 的长度为 (x-1) m.
在 Rt△ACE 中，∠AEC = 90°，
由勾股定理得 AE2 + CE2 = AC2，
即 (x - 1)2 + 32 = x2，解得x=5.
故滑道 AC 的长度为 5 m.
【课本P14 随堂练习】
甲、乙两位探险者到沙漠进行探险. 某日早晨 8:00 甲先出发，他以 6 km/h 的速度向正东行走. 1 h 后乙出发，他以 5 km/h 的速度向正北行走. 上午10:00，甲、乙二人相距多远？
解：由题意可画出如图所示的图形，设甲、乙二人出发点为C，甲向东行走2h到B，乙向北行走1h到A，求A，B间距离.
由题意知，AC与BC夹角为90°，AC=1×5=5(km)，BC=2×6=12(km)，由勾股定理得AB2=AC2+BC2=52+122=169，则AB=13km.所以上午10:00，甲、乙二人相距13km.
1. 如图①，有一个圆柱形油罐，要从点 A 开始环绕油罐建梯子，终点正好建在点 A 的正上方点 B 处，已知油罐的底面半径是 2 m，高 AB 是 5 m. 梯子最短需要多少米？（ π 取 3 ）
解：将油罐的侧面沿 AB 剪开展成一个平面图形如图②所示，则 AB′ 为梯子的最短长度，∠A′ ＝ 90°.由题意，得 AA′ ＝ 2×3×2 ＝ 12 (m)，A′B′ ＝ 5 m.在 Rt△AA′B′ 中，由勾股定理，得AB′2 ＝ A′B′2 ＋AA′2 ＝52 ＋122 ＝ 169，所以 AB′ ＝ 13 m，即梯子最短需要 13 m.
2. 如图是王叔叔建房时所挖地基的平面图，按标准四边形 ABCD 四个角都应是直角，他在挖完后测量发现 AB ＝ CD ＝ 6 m，AD ＝ BC ＝8 m，AC ＝ BD ＝10 m，请你帮他看一下挖的地基是否合格.
解：因为 AD2 ＋ CD2 ＝82 ＋62 ＝ 100 ＝102 ＝AC2，所以△ACD 是直角三角形，∠ADC ＝ 90°.同理，∠BAD ＝∠ABC ＝∠BCD ＝ 90°，所以四边形ABCD 四个角都是直角，所以王叔叔所挖的地基合格.
立体图形中两点之间的最短路程问题
勾股定理的实际应用问题