



还剩30页未读,
继续阅读
所属成套资源:北师数学八年级上册PPT课件
成套系列资料,整套一键下载
北师数学八年级上册 第三章 章末复习 PPT课件
展开
这是一份北师数学八年级上册 第三章 章末复习 PPT课件,共38页。
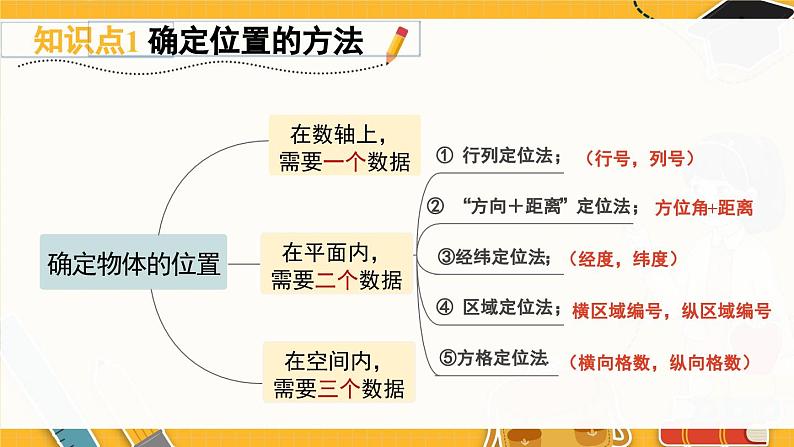
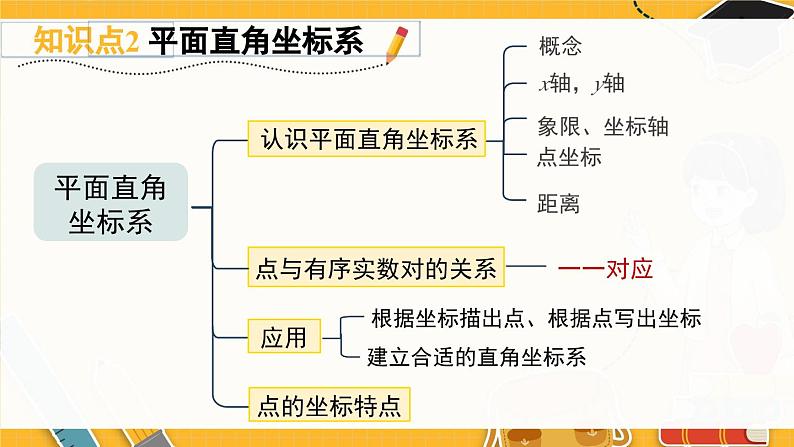
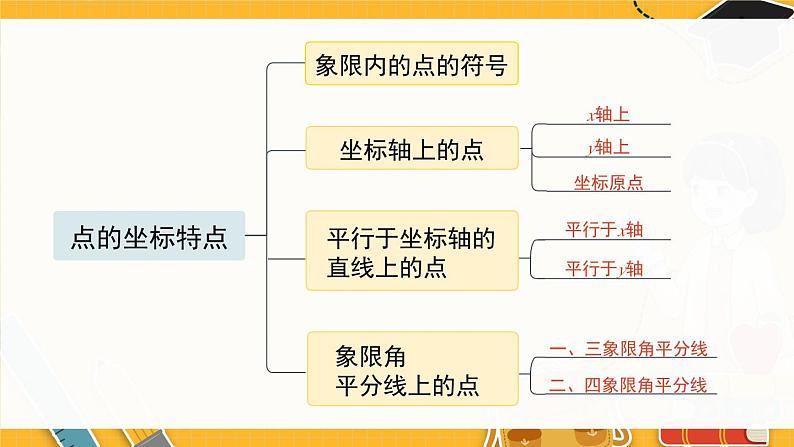
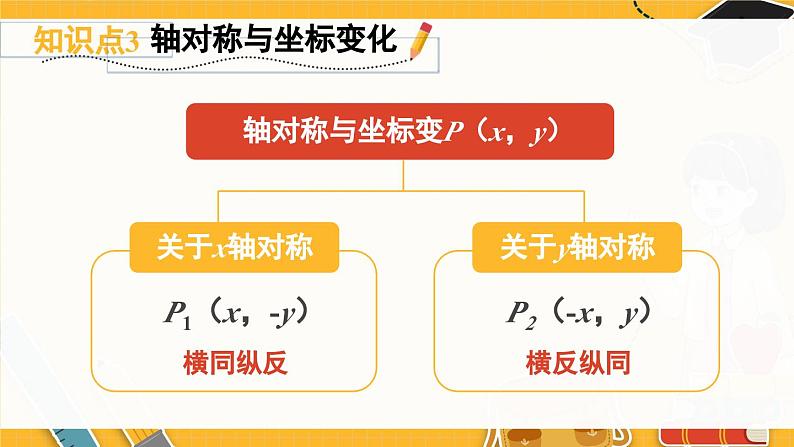
感受多种确定位置的方法,形成一定的空间观念.认识平面直角坐标系,并借助平面直角坐标系来确定物体的位置,形成数形结合的意识.体会轴对称与相应图形坐标的变化之间的关系.01.知识梳理确定物体的位置在数轴上,需要一个数据在平面内,需要二个数据在空间内,需要三个数据(行号,列号)方位角+距离(横向格数,纵向格数)(经度,纬度)横区域编号,纵区域编号平面直角坐标系 认识平面直角坐标系点与有序实数对的关系一一对应概念x轴,y轴点坐标象限、坐标轴距离应用建立合适的直角坐标系根据坐标描出点、根据点写出坐标点的坐标特点点的坐标特点象限内的点的符号坐标轴上的点平行于坐标轴的直线上的点象限角平分线上的点轴对称与坐标变P(x,y)横同纵反P1(x,-y)横反纵同P2(-x,y)02.典例剖析A在一个平面内确定某个位置时需要两个数据,常见的有:行列定位法、“方位角和距离”定位法、经纬定位法等.1-1 我们规定向东和向北方向为正,如向东走4 m ,再向北走6 m ,记作(4 , 6) ,则向西走5m ,再向北走3 m ,记作__________.(-5 , 3)1-2 如图,若字母 Р 用( 2 , 3)表示,字母 N 用 (7 , 2)表示,则字母K可表示为__________ (6 , 3)表示的字母是__________.T(4 , 2)B(2)如果点A(3,m)在 x 轴上,那么点B( m-2,m-3)所在的象限是( )A.第一象限 B.第二象限C.第三象限 D.第四象限C(3)已知点 A 的坐标为( n+3,3 ),点 B 的坐标为(n-4,n),且 AB//x 轴,则线段 AB 的长为______.7D2-1 已知点 M 在x 轴上方, y 轴左侧,距离 x 轴1个单位长度,距离 y 轴4个单位长度,则点M的坐标为( )A.(1,4) B.(-1,-4) C.(4, -1) D.(-4,1)D2-2 在平面直角坐标系中,若点A( a, -b)在第一象限内,则点B(a , b)所在的象限是( )A.第一象限 B.第二象限 C.第三象限 D.第四象限 如图①,已知长方形ABCD的长为8,宽为6.(1)建立平面直角坐标系,使其中点A的坐标为(-4,3),并写出其余三个顶点的坐标;(2)以不同于(1)的方法建立适当的平面直角坐标系,并写出各点的坐标.例 3解:(1)建立平面直角坐标系如图②所示,B(-4,-3),C(4,-3),D(4,3).(2)建立平面直角坐标系如图③所示,A(-8,6), C(-8, 0), D( 0,6).(答案不唯一)3-1 如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿,将其放在平面直角坐标系中,表示叶片“顶部”A,B两点的坐标分别为( -2,2),( -3,0) ,则叶杆“底部”点C的坐标为________.(2 , -3)3-2 己知平面内有 M ,N ,P三点,以点 N 为坐标原点建立平面直角坐标系时,点 M 的坐标为(3,4),点 P 的坐标为 (4,5).若以点 M 为坐标原点建立平面直角坐标系,点 P 的坐标为(1,1) ,则点 N 的坐标为( )A.( -3,-4) B.(4,0) C.( 0,-2) D.(2,0)A(-2 , -3) 已知点A(-3,2a-1)与点B(b,﹣3)关于x轴对称,那么点P(a ,b)关于 y 轴对称的点P'的坐标为_________.例 4解析:因为点A(-3,2a-1)与点B(b,-3)关于 x 轴对称,所以b=-3,2a-1 =3,解得a=2,故P(2,-3),则点P(a , b)关于y 轴对称的点P'的坐标为(-2,-3).4-1 已知点A( -1,3)和点B在坐标平面内关于 x 轴对称,则点B的坐标是( )A.( -1,-3) B.( -1,-3)C.( 1,-3) D.( 3,-1)4-2 如图,△ABC 与△DEF关于y轴对称,已知A( -4,6) ,B(-6,2 ),E(2,1) ,则点D的坐标为( )A.(-4,6) B.(4,6)C.(-2,1) D.(6,2)AB 5-1 如图,△ABC在正方形网格中,若点A 的坐标为(0,3) ,点B的坐标为( -3,-1).(1)在图中建立平面直角坐标系;(2)作出△ABC关于 y 轴对称的图形△A'B'C',并直接写出点C'的坐标.解:(1)建立平面直角坐标系如图所示.(2)△A'B'C'如图所示,点C'的坐标为(-1,1).03.复习题1. 在直角坐标系中,写出下列各点的坐标:(1)A ( -4 ,0);(2)B ( 0 ,4);(3)C (-4 ,4).【教材P71 复习题 第1题】(1) 点 A 在 x 轴上,位于原点的左侧,距离坐标原点 4 个单位长度;(2) 点 B 在 y 轴上,位于原点的上侧,距离坐标原点 4 个单位长度;(3) 点 C 在 y 轴的左侧,在 x 轴的上侧,距离每个坐标轴都是 4 个单位长度.点(0,a)在纵轴的正半轴上;点(b,0)在横轴的正半轴上.【教材P71 复习题 第2题】长方形的两条边长分别为8,6,建立适当的直角坐标系,并写出它的四个顶点的坐标.3.答案不唯一,例如,下面是建立直角坐标系的2种方法.【教材P71 复习题 第3题】在直角坐标系中,将坐标为(0,0),(2,4),(2,0),(4,4)的点用线段依次连接起来形成一个图案.4.(1)所得图案与原图案关于纵轴对称;(2)所得图案与原图案关于横轴对称.【教材P71 复习题 第4题】(2)原图案四个点的横坐标保持不变,纵坐标分别乘-1,将所得的四个点用线段依次连接起来,这个图案与原图案又有怎样的位置关系?(1)这四个点的纵坐标保持不变,横坐标分别乘-1,将所得的四个点用线段依次连接起来,这个图案与原图案有怎样的位置关系?5.描出与下图中的枫叶图案关于x轴对称的图形的简图.【教材P71 复习题 第5题】6.在直角坐标系中,将坐标是(2,0),(2,2),(0,2),(0,3),(2,5),(3,5),(2,2),(5,3),(5,2),(3,0), (2,0)的点用线段依次连接起来形成一个图案.【教材P72 复习题 第6题】(1) 每个点的纵坐标保持不变,横坐标分别乘-1,再将所得的点用线段依次连接起来,所得的图案与原图案有怎样的位置关系?(2) 原图案每个点的横坐标保持不变,纵坐标分别乘-1,顺次连接这些点,你会得到怎样的图案?这个图案与原图案又有怎样的位置关系呢?(2,0)(2,2)(0,2)(0,3)(2,5)(3,5)(2,2)(5,3)(5,2)(3,0)(2,0)(-2,0)(-2,2)(0,2)(0,3)(-2,5)(-3,5)(-2,2)(-5,3)(-5,2)(-3,0)(-2,0)(2,0)(2,-2)(0,-2)(0,-3)(2,-5)(3,-5)(2,-2)(5,-3)(5,-2)(3,0)(2,0)(x,y)(-x,y)(x,-y)解:(1)所得图案与原图案关于纵轴对称;(2)所得图案与原图案关于横轴对称.7.某个图形上各点的纵坐标保持不变,而横坐标变为原来的相反数,此时图形却未发生任何改变.你认为这可能吗?举例说明.可能,如本身关于纵轴对称的图形(图为教材P70 第3题图).【教材P72 复习题 第7题】8.长方形的两条边长分别为4,6,建立适当的直角坐标系,使它的一个顶点的坐标为(-2,-3).与同伴进行交流,你们的答案相同吗?解:答案不唯一,举例如下.【教材P72 复习题 第8题】9. (1) 与x轴平行的直线上的点,它们的坐标之间有什么 关系?与y轴平行的直线上的点呢? (2) 如果a,b同号,则点P(a,b)在第几象限?如果a,b异 号呢?(1)与x轴平行的直线上的点,它们的纵坐标相等; 与y轴平行的直线上的点,它们的横坐标相等.(2)若a,b同号,则点P(a,b)在第一象限或第三象限; 若a,b异号,则点P(a,b)在第二象限或第四象限.【教材P72 复习题 第9题】11.在世界地图上找出位于东经120°、北纬30°附近的城市.解:杭州.(答案不唯一)【教材P72 复习题 第11题】10.试用两个数据表示学校的旗杆相对于学校大门的位置.【教材P72 复习题 第10题】12.某路公交车由实验中学出发,途经A2区、A3区、B3区、B2区、B1 区、C1区、C2区、D2区、D1区,到达博物馆.在下边的城市简图上描出它的行车路线.【教材P72 复习题 第12题】13.如图,画出与第一象限内的图形关于y轴对称的图形,你是怎样画的?它与原图中对应点的坐标有什么关系?它与原图中对应点的横坐标互为相反数,纵坐标相同.【教材P72 复习题 第13题】在如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A (0,0),B(3,6),C(14,8),D(16,0),确定这个四边形的面积.你是怎么做的?与同伴进行交流.方法不唯一,合理即可.【教材P73 复习题 第14题】14.如图为上海世博园区的一部分.【教材P73 复习题 第15题】15. (1)你能向你的同学介绍如何才能找到土库曼斯坦馆和澳门馆吗?(2)小明现在正在等候广场,他想到亚洲广场,你能告诉他该如何走吗?(3)小颖想从中国国家馆到摩洛哥馆,她该如何走呢?从课后习题中选取;完成练习册本课时的习题.课后作业
感受多种确定位置的方法,形成一定的空间观念.认识平面直角坐标系,并借助平面直角坐标系来确定物体的位置,形成数形结合的意识.体会轴对称与相应图形坐标的变化之间的关系.01.知识梳理确定物体的位置在数轴上,需要一个数据在平面内,需要二个数据在空间内,需要三个数据(行号,列号)方位角+距离(横向格数,纵向格数)(经度,纬度)横区域编号,纵区域编号平面直角坐标系 认识平面直角坐标系点与有序实数对的关系一一对应概念x轴,y轴点坐标象限、坐标轴距离应用建立合适的直角坐标系根据坐标描出点、根据点写出坐标点的坐标特点点的坐标特点象限内的点的符号坐标轴上的点平行于坐标轴的直线上的点象限角平分线上的点轴对称与坐标变P(x,y)横同纵反P1(x,-y)横反纵同P2(-x,y)02.典例剖析A在一个平面内确定某个位置时需要两个数据,常见的有:行列定位法、“方位角和距离”定位法、经纬定位法等.1-1 我们规定向东和向北方向为正,如向东走4 m ,再向北走6 m ,记作(4 , 6) ,则向西走5m ,再向北走3 m ,记作__________.(-5 , 3)1-2 如图,若字母 Р 用( 2 , 3)表示,字母 N 用 (7 , 2)表示,则字母K可表示为__________ (6 , 3)表示的字母是__________.T(4 , 2)B(2)如果点A(3,m)在 x 轴上,那么点B( m-2,m-3)所在的象限是( )A.第一象限 B.第二象限C.第三象限 D.第四象限C(3)已知点 A 的坐标为( n+3,3 ),点 B 的坐标为(n-4,n),且 AB//x 轴,则线段 AB 的长为______.7D2-1 已知点 M 在x 轴上方, y 轴左侧,距离 x 轴1个单位长度,距离 y 轴4个单位长度,则点M的坐标为( )A.(1,4) B.(-1,-4) C.(4, -1) D.(-4,1)D2-2 在平面直角坐标系中,若点A( a, -b)在第一象限内,则点B(a , b)所在的象限是( )A.第一象限 B.第二象限 C.第三象限 D.第四象限 如图①,已知长方形ABCD的长为8,宽为6.(1)建立平面直角坐标系,使其中点A的坐标为(-4,3),并写出其余三个顶点的坐标;(2)以不同于(1)的方法建立适当的平面直角坐标系,并写出各点的坐标.例 3解:(1)建立平面直角坐标系如图②所示,B(-4,-3),C(4,-3),D(4,3).(2)建立平面直角坐标系如图③所示,A(-8,6), C(-8, 0), D( 0,6).(答案不唯一)3-1 如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿,将其放在平面直角坐标系中,表示叶片“顶部”A,B两点的坐标分别为( -2,2),( -3,0) ,则叶杆“底部”点C的坐标为________.(2 , -3)3-2 己知平面内有 M ,N ,P三点,以点 N 为坐标原点建立平面直角坐标系时,点 M 的坐标为(3,4),点 P 的坐标为 (4,5).若以点 M 为坐标原点建立平面直角坐标系,点 P 的坐标为(1,1) ,则点 N 的坐标为( )A.( -3,-4) B.(4,0) C.( 0,-2) D.(2,0)A(-2 , -3) 已知点A(-3,2a-1)与点B(b,﹣3)关于x轴对称,那么点P(a ,b)关于 y 轴对称的点P'的坐标为_________.例 4解析:因为点A(-3,2a-1)与点B(b,-3)关于 x 轴对称,所以b=-3,2a-1 =3,解得a=2,故P(2,-3),则点P(a , b)关于y 轴对称的点P'的坐标为(-2,-3).4-1 已知点A( -1,3)和点B在坐标平面内关于 x 轴对称,则点B的坐标是( )A.( -1,-3) B.( -1,-3)C.( 1,-3) D.( 3,-1)4-2 如图,△ABC 与△DEF关于y轴对称,已知A( -4,6) ,B(-6,2 ),E(2,1) ,则点D的坐标为( )A.(-4,6) B.(4,6)C.(-2,1) D.(6,2)AB 5-1 如图,△ABC在正方形网格中,若点A 的坐标为(0,3) ,点B的坐标为( -3,-1).(1)在图中建立平面直角坐标系;(2)作出△ABC关于 y 轴对称的图形△A'B'C',并直接写出点C'的坐标.解:(1)建立平面直角坐标系如图所示.(2)△A'B'C'如图所示,点C'的坐标为(-1,1).03.复习题1. 在直角坐标系中,写出下列各点的坐标:(1)A ( -4 ,0);(2)B ( 0 ,4);(3)C (-4 ,4).【教材P71 复习题 第1题】(1) 点 A 在 x 轴上,位于原点的左侧,距离坐标原点 4 个单位长度;(2) 点 B 在 y 轴上,位于原点的上侧,距离坐标原点 4 个单位长度;(3) 点 C 在 y 轴的左侧,在 x 轴的上侧,距离每个坐标轴都是 4 个单位长度.点(0,a)在纵轴的正半轴上;点(b,0)在横轴的正半轴上.【教材P71 复习题 第2题】长方形的两条边长分别为8,6,建立适当的直角坐标系,并写出它的四个顶点的坐标.3.答案不唯一,例如,下面是建立直角坐标系的2种方法.【教材P71 复习题 第3题】在直角坐标系中,将坐标为(0,0),(2,4),(2,0),(4,4)的点用线段依次连接起来形成一个图案.4.(1)所得图案与原图案关于纵轴对称;(2)所得图案与原图案关于横轴对称.【教材P71 复习题 第4题】(2)原图案四个点的横坐标保持不变,纵坐标分别乘-1,将所得的四个点用线段依次连接起来,这个图案与原图案又有怎样的位置关系?(1)这四个点的纵坐标保持不变,横坐标分别乘-1,将所得的四个点用线段依次连接起来,这个图案与原图案有怎样的位置关系?5.描出与下图中的枫叶图案关于x轴对称的图形的简图.【教材P71 复习题 第5题】6.在直角坐标系中,将坐标是(2,0),(2,2),(0,2),(0,3),(2,5),(3,5),(2,2),(5,3),(5,2),(3,0), (2,0)的点用线段依次连接起来形成一个图案.【教材P72 复习题 第6题】(1) 每个点的纵坐标保持不变,横坐标分别乘-1,再将所得的点用线段依次连接起来,所得的图案与原图案有怎样的位置关系?(2) 原图案每个点的横坐标保持不变,纵坐标分别乘-1,顺次连接这些点,你会得到怎样的图案?这个图案与原图案又有怎样的位置关系呢?(2,0)(2,2)(0,2)(0,3)(2,5)(3,5)(2,2)(5,3)(5,2)(3,0)(2,0)(-2,0)(-2,2)(0,2)(0,3)(-2,5)(-3,5)(-2,2)(-5,3)(-5,2)(-3,0)(-2,0)(2,0)(2,-2)(0,-2)(0,-3)(2,-5)(3,-5)(2,-2)(5,-3)(5,-2)(3,0)(2,0)(x,y)(-x,y)(x,-y)解:(1)所得图案与原图案关于纵轴对称;(2)所得图案与原图案关于横轴对称.7.某个图形上各点的纵坐标保持不变,而横坐标变为原来的相反数,此时图形却未发生任何改变.你认为这可能吗?举例说明.可能,如本身关于纵轴对称的图形(图为教材P70 第3题图).【教材P72 复习题 第7题】8.长方形的两条边长分别为4,6,建立适当的直角坐标系,使它的一个顶点的坐标为(-2,-3).与同伴进行交流,你们的答案相同吗?解:答案不唯一,举例如下.【教材P72 复习题 第8题】9. (1) 与x轴平行的直线上的点,它们的坐标之间有什么 关系?与y轴平行的直线上的点呢? (2) 如果a,b同号,则点P(a,b)在第几象限?如果a,b异 号呢?(1)与x轴平行的直线上的点,它们的纵坐标相等; 与y轴平行的直线上的点,它们的横坐标相等.(2)若a,b同号,则点P(a,b)在第一象限或第三象限; 若a,b异号,则点P(a,b)在第二象限或第四象限.【教材P72 复习题 第9题】11.在世界地图上找出位于东经120°、北纬30°附近的城市.解:杭州.(答案不唯一)【教材P72 复习题 第11题】10.试用两个数据表示学校的旗杆相对于学校大门的位置.【教材P72 复习题 第10题】12.某路公交车由实验中学出发,途经A2区、A3区、B3区、B2区、B1 区、C1区、C2区、D2区、D1区,到达博物馆.在下边的城市简图上描出它的行车路线.【教材P72 复习题 第12题】13.如图,画出与第一象限内的图形关于y轴对称的图形,你是怎样画的?它与原图中对应点的坐标有什么关系?它与原图中对应点的横坐标互为相反数,纵坐标相同.【教材P72 复习题 第13题】在如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A (0,0),B(3,6),C(14,8),D(16,0),确定这个四边形的面积.你是怎么做的?与同伴进行交流.方法不唯一,合理即可.【教材P73 复习题 第14题】14.如图为上海世博园区的一部分.【教材P73 复习题 第15题】15. (1)你能向你的同学介绍如何才能找到土库曼斯坦馆和澳门馆吗?(2)小明现在正在等候广场,他想到亚洲广场,你能告诉他该如何走吗?(3)小颖想从中国国家馆到摩洛哥馆,她该如何走呢?从课后习题中选取;完成练习册本课时的习题.课后作业
相关资料
更多









