




专题2.5 二次函数与线段最值面积最值综合应用(四大题型)(含答案)2023-2024学年九年级数学上册《重难点题型 高分突破》(人教版)
展开【题型1 线段差最大问题】
【题型2 线段和最小】
【题型3 周长最值问题】
【题型4 求面积最值】
【题型1 线段差最大问题】
【典例1】(2023•汝南县一模)如图,已知抛物线过点O(0,0),A(5,5),其对称轴为x=2.
(1)求该抛物线的解析式;
(2)若点B是抛物线对称轴上的一点,且点B在第一象限.
①当△OAB的面积为15时,求点B的坐标;
②在①的条件下,P是抛物线上的动点,当PA﹣PB取得最大值时,求点P的坐标.
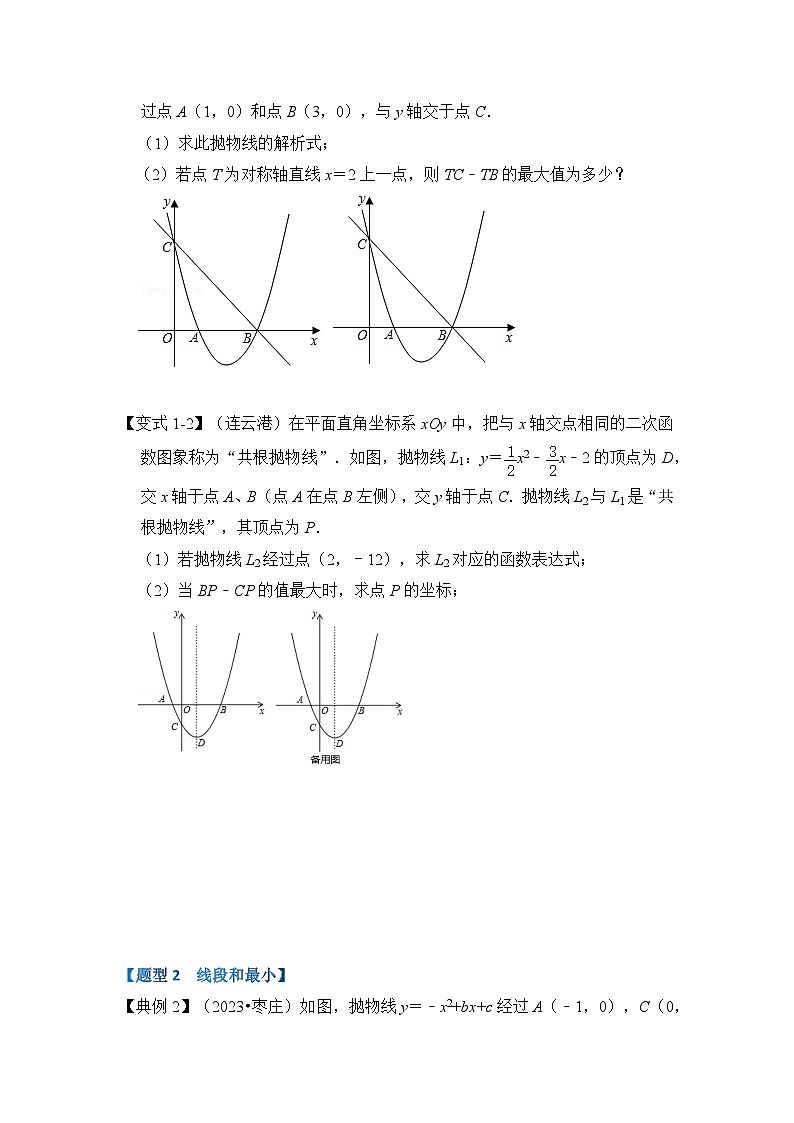
【变式1-1】(秋•椒江区校级月考)如图,已知抛物线y=ax2+bx+3(a≠0)经过点A(1,0)和点B(3,0),与y轴交于点C.
(1)求此抛物线的解析式;
(2)若点T为对称轴直线x=2上一点,则TC﹣TB的最大值为多少?
【变式1-2】(连云港)在平面直角坐标系xOy中,把与x轴交点相同的二次函数图象称为“共根抛物线”.如图,抛物线L1:y=x2﹣x﹣2的顶点为D,交x轴于点A、B(点A在点B左侧),交y轴于点C.抛物线L2与L1是“共根抛物线”,其顶点为P.
(1)若抛物线L2经过点(2,﹣12),求L2对应的函数表达式;
(2)当BP﹣CP的值最大时,求点P的坐标;
【题型2 线段和最小】
【典例2】(2023•枣庄)如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),C(0,3)两点,并交x轴于另一点B,点M是抛物线的顶点,直线AM与y轴交于点D.
(1)求该抛物线的表达式;
(2)若点H是x轴上一动点,分别连接MH,DH,求MH+DH的最小值;
【变式2-1】(2023•河南三模)如图,抛物线交x轴于点A,B,交y轴于点C,连接AC,点A的坐标为(﹣2,0),抛物线的对称轴为直线x=1.
(1)求抛物线的表达式和顶点坐标;
(2)在直线x=1上找一点P,使PA+PC的和最小,并求出点P的坐标;
【变式2-2】(2022秋•常德期末)如图,二次函数y=ax2﹣2x+c(a≠0)的图象交x轴于点A(﹣3,0),B(1,0),交y轴于点C,顶点为D.
(1)求二次函数的解析式;
(2)点P是抛物线的对称轴上一个动点,连接BP,CP,当BP+CP的长度最小时,求出点P的坐标;
【变式2-3】(2023•中宁县二模)如图,抛物线y=x2+bx+c的对称轴为直线x=2,与x轴交于A,B两点,与y轴交于C点,且A点坐标为(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)点M(a,0)是x轴上的一个动点,当CM+DM的值最小时,求a的值.
【变式2-4】(2023•太康县模拟)如图,抛物线y=ax2+bx+2交y轴于点C,交x轴于A(﹣1,0),B(4,0)两点,作直线BC.
(1)求抛物线的函数表达式;
(2)在抛物线的对称轴上找一点P,使PC+PA的值最小,求点P的坐标;
【题型3 周长最值问题】
【典例3】(2023•张家界)如图,在平面直角坐标系中,已知二次函数y=ax2+bx+c的图象与x轴交于点A(﹣2,0)和点B(6,0)两点,与y轴交于点C(0,6).点D为线段BC上的一动点.
(1)求二次函数的表达式;
(2)如图1,求△AOD周长的最小值;
【变式3-1】(2023•盘锦三模)如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
(1)求抛物线的函数表达式;
(2)设P为对称轴上一动点,求△APC周长的最小值;
【变式3-2】(2023春•民乐县校级月考)已知抛物线y=﹣x2+bx+c与x轴交于A(﹣2,0),B(1,0)两点,与y轴交于点C,连接AC,点P是AC上方抛物线上一点.
(1)求抛物线的解析式;
(2)在抛物线对称轴有一点Q,使△QBC的周长最小,求Q的坐标;
【变式3-3】(2022•齐河县模拟)如图1,抛物线y=ax2+bx+3过A(1,0)、B(3,0)两点,交y轴于点C.
(1)求抛物线的函数解析式;
(2)在抛物线的对称轴上是否存在点M,使△ACM的周长最小?若存在,求出△ACM周长的最小值;若不存在,请说明理由.
【题型4 求面积最值】
【典例4】(2023•利津县一模)综合与实践
如图,抛物线y=2x2﹣4x﹣6与x轴交于A,B两点,且点A在点B的左侧,与y轴交于点C,点D是抛物线上的一动点.
(1)求A,B,C三点的坐标;
(2)如图2,当点D在第四象限时,连接BD,CD和BC,得到△BCD,当△BCD的面积最大时,求点D的坐标;
【变式4-1】(2022秋•金华期末)已知抛物线y=﹣x2﹣bx+c的图象与x轴交于点A(﹣3,0)和点C,与y轴交于点B(0,3).
(1)求抛物线的解析式;
(2)设点P为抛物线的对称轴上一动点,当△PBC的周长最小时,求点P的坐标;
(3)在第二象限的抛物线上,是否存在一点Q,使得△ABQ的面积最大?若存在,求出点Q的坐标;若不存在,请说明理由.
【变式4-2】(2023•娄底模拟)如图1,若二次函数y=ax2+bx+4的图象与x轴交于点A(﹣1,0)、B(4,0),与y轴交于点C,连接AC、BC.
(1)求二次函数的解析式;
(2)若点P是抛物线在第一象限上一动点,连接PB、PC,当△PBC的面积最大时,求出点P的坐标;
【变式4-3】(2023•晋中模拟)综合与探究
如图,抛物线y=﹣x2+bx+c的顶点为D(1,4),与x轴交于A和B两点,交y轴于点C.
(1)求抛物线的函数表达式及点A,B、C的坐标;
(2)如图1,点P是直线BC上方的抛物线上的动点,当△BCP面积最大时,求点P的横坐标;
【变式4-4】(2022秋•南川区期末)如图1,在平面直角坐标系中,二次函数y=ax2+bx﹣3(a≠0)的图象与x轴于A(﹣1,0),B(3,0)两点,与y轴交于C点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)当动点P运动到什么位置时,使四边形ACPB的面积最大,求出此时四边形ACPB的面积最大值和P的坐标;
【变式4-5】(2022秋•渝北区期末)如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C点.
(1)求抛物线的函数表达式;
(2)点P是直线BC下方抛物上一动点,连接PB,PC,求△PBC面积的最大值以及此时点P的坐标;
【变式4-6】(2023春•青秀区校级期末)如图所示,已知抛物线y=ax2+bx+5(a<0)与x轴交于点A(﹣1,0)和点B(5,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)点P为抛物线上的一个动点,且在直线BC上方,试求出△BCP面积的最大值;
【变式4-7】(2023•仁怀市模拟)如图1,在平面直角坐标系中,直线y=﹣x+4交两坐标轴于B、C两点,二次函数y=ax2+bx+c图象经过A,B,C三点且A(﹣1,0).
(1)求二次函数的解析式.
(2)在抛物线的对称轴上是否存在点P?使得PA+PC的长度最短.若存在,求出点P的坐标;若不存在,请说明理由.
(3)在直线上方抛物线上是否存在点Q?使得△QBC的面积有最大值.若存在,求出点Q的坐标及此时△QBC的面积;若不存在,请说明理由.
【变式4-8】(2023•德惠市校级模拟)如图,在平面直角坐标系中,一次函数y=kx+b与二次函数y=﹣x2+mx+n交于点A(3,0),B(0,3)两点.
(1)求一次函数y=kx+b和二次函数y=﹣x2+mx+n的解析式.
(2)点P是二次函数图象上一点,且位于直线AB上方,过点P作y轴的平行线,交直线AB于点Q,当△PAB面积最大时,求点P的坐标.
【变式4-9】(2023•资兴市二模)如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,过点A的直线L交抛物线于点C(2,m).
(1)求抛物线的解析式;
(2)若点P是直线AC下方抛物线y=x2+bx+c的一个动点,当△PAC面积最大时,求点P的坐标及△PAC面积最大值.
【变式4-10】(2023•顺德区模拟)如图,抛物线y=﹣x2+bx+c交直线y=﹣x+4于坐标轴上B,C两点,交x轴于另一点A,连接AC.
(1)求抛物线的解析式;
(2)点D为线段BC上一点,过点D作直线l∥AC,交x轴于点E.
连接AD,求△ADE面积的最大值;
专题04 二次函数的最值问题专训-2023-2024学年九年级数学上册重难点高分突破(浙教版): 这是一份专题04 二次函数的最值问题专训-2023-2024学年九年级数学上册重难点高分突破(浙教版),文件包含专题04二次函数的最值问题专训原卷版docx、专题04二次函数的最值问题专训解析版docx等2份试卷配套教学资源,其中试卷共71页, 欢迎下载使用。
最新中考数学重难点与压轴题型训练(讲义) 专题18 二次函数中线段、周长、面积最值问题(重点突围): 这是一份最新中考数学重难点与压轴题型训练(讲义) 专题18 二次函数中线段、周长、面积最值问题(重点突围),文件包含专题18二次函数中线段周长面积最值问题重点突围原卷版docx、专题18二次函数中线段周长面积最值问题重点突围解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
专题2.5 二次函数与线段最值面积最值综合应用(四大题型)-2023-2024学年九年级数学上册期末复习《重难点题型》(人教版): 这是一份专题2.5 二次函数与线段最值面积最值综合应用(四大题型)-2023-2024学年九年级数学上册期末复习《重难点题型》(人教版),文件包含专题25二次函数与线段最值面积最值综合应用四大题型原卷版docx、专题25二次函数与线段最值面积最值综合应用四大题型解析版docx等2份试卷配套教学资源,其中试卷共45页, 欢迎下载使用。












