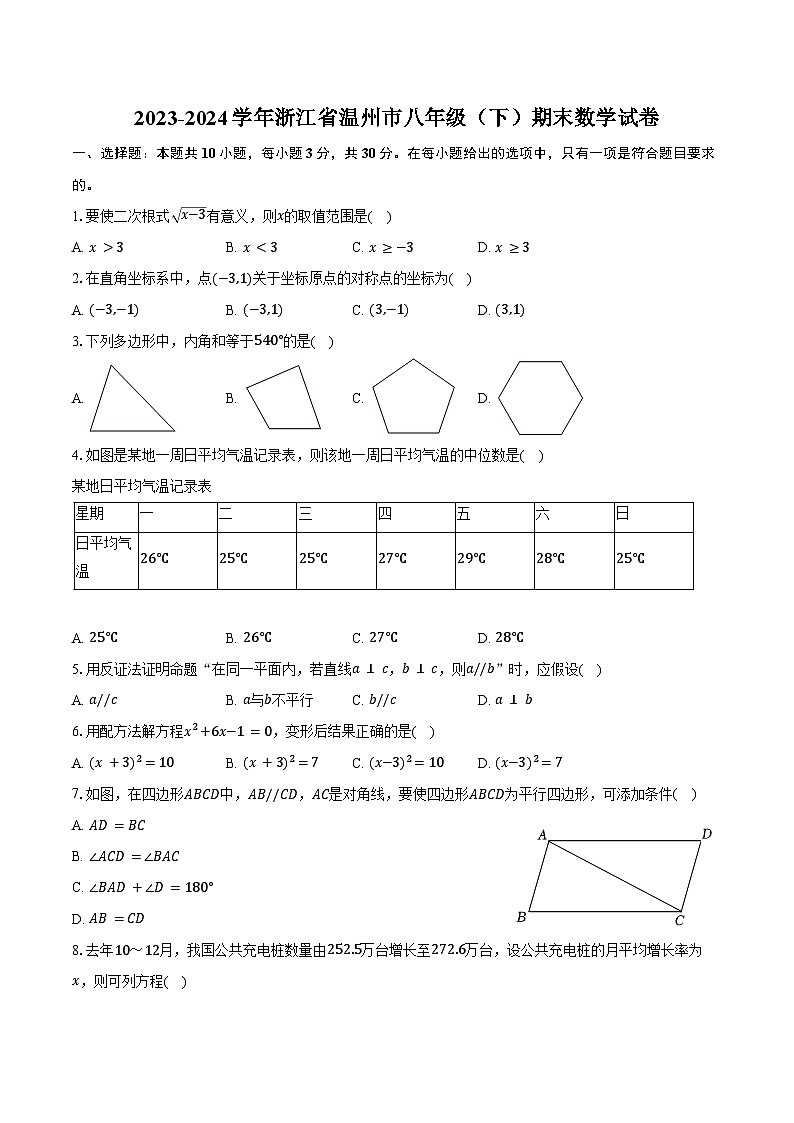
2023-2024学年浙江省温州市八年级（下）期末数学试卷（含答案）

这是一份2023-2024学年浙江省温州市八年级（下）期末数学试卷（含答案），共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.要使二次根式 x−3有意义，则x的取值范围是( )
A. x>3B. x<3C. x≥−3D. x≥3
2.在直角坐标系中，点(−3,1)关于坐标原点的对称点的坐标为( )
A. (−3,−1)B. (−3,1)C. (3,−1)D. (3,1)
3.下列多边形中，内角和等于540°的是( )
A. B. C. D.
4.如图是某地一周日平均气温记录表，则该地一周日平均气温的中位数是( )
某地日平均气温记录表
A. 25℃B. 26℃C. 27℃D. 28℃
5.用反证法证明命题“在同一平面内，若直线a⊥c，b⊥c，则a/​/b”时，应假设( )
A. a/​/cB. a与b不平行C. b/​/cD. a⊥b
6.用配方法解方程x2+6x−1=0，变形后结果正确的是( )
A. (x+3)2=10B. (x+3)2=7C. (x−3)2=10D. (x−3)2=7
7.如图，在四边形ABCD中，AB/​/CD，AC是对角线，要使四边形ABCD为平行四边形，可添加条件( )
A. AD=BC
B. ∠ACD=∠BAC
C. ∠BAD+∠D=180°
D. AB=CD
8.去年10～12月，我国公共充电桩数量由252.5万台增长至272.6万台，设公共充电桩的月平均增长率为x，则可列方程( )
A. 252.5(1+x)2=272.6B. 252.5(1+x2)=272.6
C. 252.5(1+2x)=272.6D. 252.5x2=272.6
9.已知点(− 2,y1)，(−1,y2)，( 3,y3)在函数y= 6x的图象上，则( )
A. y110.如图，在矩形ABCD中，E，F分别是边AD，CD上的点，且AEA. 5+12B. 3C. 85D. 53
二、填空题：本题共6小题，每小题3分，共18分。
11.当x=1时，二次根式 5+4x的值是______．
12.小明同学对篮球、排球、足球三种中考球类项目分别进行10次测试，发现成绩平均分都相同，方差如下：S篮球2=4.2，S排球2=3.2，S足球2=9，则发挥最稳定的项目是______．
13.从地面竖直向上抛出一小球，t(秒)后小球的高度ℎ(米)适用公式ℎ=30t−5t2，那么经过______秒后，小球回到地面．
14.如图，已知菱形ABCD的顶点A和B的坐标分别为(−2,0)、(3,0)，点C在y轴的正半轴上.则点D的坐标是______．
15.如图，正方形ABCD的顶点A，B在x轴上，反比例函数y=kx(k>0)的图象经过点D和BC的中点E.若AB=3，则k的值是______．
16.如图1是一款风筝，图2是其骨架示意图，A，B，C，D是正方形的四个顶点，点E，F在AB中垂线上，∠EAB=∠FDC=45°，AF，DE交于点G，CE，BF交于点H.若AB=10dm，BC=7dm，则骨架总长(图2中所有实线之和)为______dm．
三、解答题：本题共7小题，共52分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题8分)
(1)计算： 8− 6× 3；
(2)解方程：x2−4x=0．
18.(本小题6分)
如图，在等腰△ABC中，AB=AC．
(1)用直尺和圆规在平面上作点D，使得A，B，C，D为顶点的四边形是菱形，并作出这个菱形.(不写作法，保留作图痕迹)
(2)若AB=3，BC=2，求(1)中所作菱形对角线AD的长．
19.(本小题6分)
学校广播台要招聘一名编辑，甲、乙、丙三位同学报名并参加了3项素质测试，成绩如下表(单位：分)．
(1)计算得甲、乙的平均分分别为80分，79分，请求出丙的平均分，并根据三人的平均分从高到低进行排序．
(2)学校认为：
①单项最低分不能低于75分；
②三个项目的重要程度有所不同，每位应聘者的语言文字能力、运用媒体能力、创意设计能力的成绩应按5：2：3的比例计算其成绩.请问谁能成功应聘？
20.(本小题7分)
如图，已知▱ABCD，延长AB至点E，使BE=AB，连结CE，DE．
(1)求证：四边形BECD是平行四边形．
(2)当∠A=∠ADB时，求证：BC⊥DE．
21.(本小题7分)
已知一元二次方程x2+bx+c=0．
(1)当b=2时，若方程的一个根为−3，求c的值以及方程的另一个根．
(2)当c+1=14b2时，请判别方程根的情况．
22.(本小题8分)
综合与实践：探索某款冷柜的日耗电量．
素材1：图1是某款冷柜，耗电功率为0.15千瓦.当内部温度为−4℃时，冷柜运行，当温度下降到−20℃时，停止运行，温度上升，到−4℃时，冷柜再次运行，如此循环．
素材2：冷柜内部温度y(℃)与时间x(min)的关系如图2所示．
当0≤x≤4时，y是x的一次函数；当4≤x≤t时，y是x的反比例函数．
链接：冷柜每天耗电量(度)=耗电功率(千瓦)×每天运行时间(小时)．
任务1：求4≤x≤t时，y关于x的函数表达式．
任务2：求该冷柜一天的耗电量．
23.(本小题10分)
如图，正方形ABCD的边长为2，点E在边BC上，BE的中垂线分别交AC，BC于点P，N，延长CB至点F，使BF=12CE，连结PD，PE，PF．
(1)求证：PE=PD．
(2)设CE=a(a>0)，四边形CDPE的面积S．
①用含a的代数式表示S．
②当△PEF为等腰三角形时，求S的值．
参考答案
1.D
2.C
3.C
4.B
5.D
6.A
7.D
8.A
9.B
10.D
11.3
12.排球
13.6
14.(−5,4)
15.9
16.(59+10 2)
17.解：(1) 8− 6× 3=2 2− 3×6=2 2−3 2=− 2；
(2)x2−4x=0．
x(x−4)=0，
x1=0，x2=4，
18.解：(1)如图，分别以点B，C为圆心，AB的长为半径画弧，两弧在点A的异侧相交于点D，连接BD，CD，
则四边形ABDC即为所求．

(2)连接AD，交BC于点O，
∵四边形ABDC为菱形，
∴AD⊥BC，BO=12BC=1，AD=2OA，
在Rt△AOB中，由勾股定理得，OA= AB2−OB2= 32−12=2 2，
∴AD=2OA=4 2．
19.解：(1)丙的平均分=80+78+853=81(分)，
∵甲乙丙三人的平均分分别是80，79，81．
∴81>80>79；
(2)因为乙的创意设计能力不合格，所以乙首先被淘汰，
甲的加权平均分是：86×5+77×2+77×35+2+3=81.5(分)，
丙的加权平均分是：80×5+78×2+85×35+2+3=81.1(分)，
因为甲的加权平均分最高，所以甲将成功应聘．
20.证明：(1)∵四边形ABCD是平行四边形，
∴AB/​/CD，AB=CD，
∵BE=AB，
∴BE=CD，
∴四边形BECD是平行四边形；
(2)由(1)可知，四边形BECD是平行四边形，
∵∠A=∠ADB，
∴DB=AB，
∵BE=AB，
∴DB=BE，
∴平行四边形BECD是菱形，
∴BC⊥DE．
21.解：(1)将b=2，x=−3代入原方程得，
(−3)2−3×2+c=0，
解得c=−3，
所以原方程为x2+2x−3=0，
解得x1=1，x2=−3，
所以方程的另一个根为1．
(2)由所给一元二次方程可知，
Δ=b2−4c．
因为c+1=14b2，
所以b2=4c+4，
所以Δ=4c+4−4c=4>0，
所以方程有两个不相等的实数根．
22.解：任务1，设反比例函数解析式为y=kx，(4,−20)在函数图象上，
∴k=−80，
∴y关于x的函数表达式为y=−80x(4≤x≤t)；
任务2，由任务1可知，反比例函数解析式为y=−80x，
当y=−4时，t=20，
∴该冷柜一个循环耗时20分钟．一个循环运行4分钟，一小时运行12分钟，一天运行24×12=288分钟
288分钟等于245小时，
∴该冷柜一天的耗电量0.15×245=0.72(度)．
答：该冷柜一天的耗电0.72度．
23.(1)证明：连结PB．

∵PN垂直平分BE，
∴PE=PB，
又∵P为正方形ABCD对角线上一点，
由正方形的轴对称性得：PD=PB，
∴PE=PD；
(2)解：①如图，作PM⊥CD于点M，

∵PN垂直平分BE，
∴∠PNE=∠PMD=90°，
又∵P为正方形ABCD对角线AC上一点，
∴AC平分∠BCD，
∴PN=PМ=СN=1+a2，
∴S=S△PCE+S△PCD=12a(1+a2)+12×2(1+a2)=1+a+14a2，
∴S=1+a+14a2；
②∵PF>PB=PE，
∴△PEF为等腰三角形分两种情况：
当FP=FE时，即FP2=FE2，
∴12+(1+a2)2=(2−a2)2，
解得：a=23，
∴S=(1+a2)2=(1+13)2=169，
当PE=EF时，即PE2=EF2，
∴(2−a2)2=(1+a2)2+(1−a2)2，
化简得：a2+8a−8=0，
解得：a=−4±2 6，
∵a>0，
∴a=−4+2 6，
∴S=(1+a2)2=(1−2+ 6)2=7−2 6，
综上可得：S=169或7−2 6． 星期
一
二
三
四
五
六
日
日平均气温
26℃
25℃
25℃
27℃
29℃
28℃
25℃
语言文字能力
运用媒体能力
创意设计能力
甲
86
77
77
乙
76
87
74
丙
80
78
85