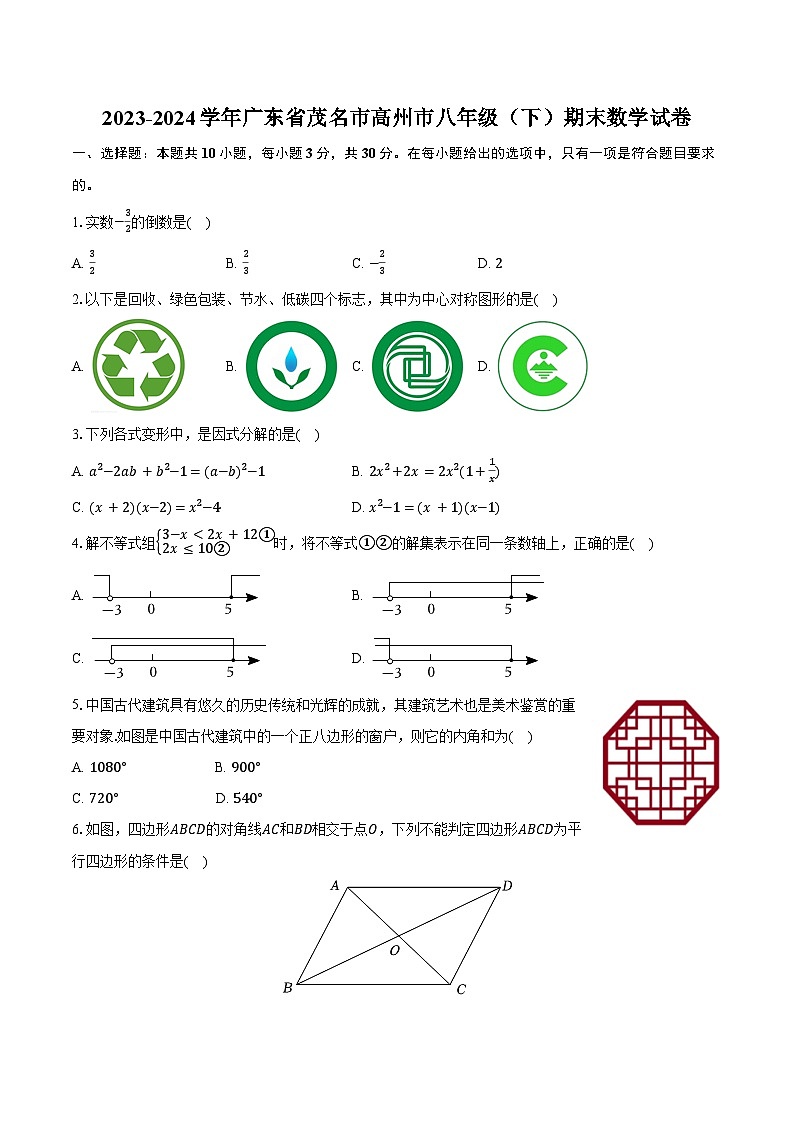
2023-2024学年广东省茂名市高州市八年级（下）期末数学试卷（含答案）

这是一份2023-2024学年广东省茂名市高州市八年级（下）期末数学试卷（含答案），共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.实数−32的倒数是( )
A. 32B. 23C. −23D. 2
2.以下是回收、绿色包装、节水、低碳四个标志，其中为中心对称图形的是( )
A. B. C. D.
3.下列各式变形中，是因式分解的是( )
A. a2−2ab+b2−1=(a−b)2−1B. 2x2+2x=2x2(1+1x)
C. (x+2)(x−2)=x2−4D. x2−1=(x+1)(x−1)
4.解不等式组3−x01−12x≥0，并求不等式组最小的整数解；
(2)解方程：1x−1+1=32x−2．
17.(本小题7分)
定义：对角线互相垂直的四边形叫做“垂美”四边形.现有如图所示的“垂美”四边形ABCD，对角线AC，BD相交于点O，若AB=5，CD=6，求AD2+BC2．
18.(本小题7分)
在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上，请解答下列问题：
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1，并写出点C1的坐标；
(2)作出△ABC关于原点O对称的△A2B2C2，并写出点C2的坐标；
(3)△A2B2C2可看作△A1B1C1以点(______，______)为旋转中心，旋转180°得到的．
19.(本小题9分)
【教材呈现】如图是华师版八年级下册数学教材第77页的部分内容．
(1)请根据教材提示，结合图1，写出完整的证明过程．
(2)【性质应用】如图2，在▱ABCD中，对角线AC，BD相交于点O，EF过点O且与边AD，BC分别相交于点E，F.求证：OE=OF．
(3)【拓展提升】在【性质应用】的条件下，连接AF.若EF⊥AC，△ABF的周长是9，则▱ABCD的周长是______．
20.(本小题9分)
某校开设智能机器人编程的校本课程，购买了A，B两种型号的机器人模型.A型机器人模型单价比B型机器人模型单价多200元，用2000元购买A型机器人模型和用1200元购买B型机器人模型的数量相同．
(1)求A型，B型机器人模型的单价分别是多少元？
(2)学校准备再次购买A型和B型机器人模型共40台，购买B型机器人模型不超过A型机器人模型的3倍.问购买A型和B型机器人模型各多少台时花费最少？最少花费是多少元？
21.(本小题9分)
在Rt△ABC中，∠BAC=90°，E，F分别是BC，AC的中点，延长BA到点D，使得AB=2AD，连接DE，DF，AE，EF，AF于DE交于点O．
(1)证明：AF与DE互相平分；
(2)如果AB=6，BC=10，求DO的长．
22.(本小题12分)
如图，在平面直角坐标系xOy中，已知点A(52,2)，B(4,0)
(1)求直线AB的表达式；
(2)在x轴上找出所有的点C，使△ABC是以线段AB为腰的等腰三角形；
(3)是否存在点P、Q，满足点P在x轴上，点Q在y轴上，且以A，B，P，Q为顶点的四边形是平行四边形，若存在，试求出点P、Q的坐标；若不存在，试说明理由．
23.(本小题12分)
已知正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB，DC(或它们的延长线)于M，N．

(1)当∠MAN绕点A旋转到BM=DN时(如图1所示)，并将△ABM逆时针旋转90°，得到△ABM′，求证BM+DN=MN；
(2)当∠MAN绕点A旋转到BM≠DN时(如图2所示)，线段BM，DN和MN之间有怎样的数量关系？写出猜想，并加以证明；
(3)当∠MAN绕点A旋转到(如图3所示)的位置时，线段BM，DN和MN之间又有怎样的数量关系？请直接写出你的猜想．
参考答案
1.C
2.C
3.D
4.C
5.A
6.C
7.B
8.B
9.D
10.C
11.a(3a−2)
12.35°
13.m0①1−12x≥0②，
由①得x>−1，
由②得x≤2，
∴不等式组的解集为−10，
∴w随m的减小而减小．
当m=10时，w取得最小值14000，
∴40−m=30，
答：购买A型机器人模型10台和B型机器人模型30台时花费最少，最少花费是14000元．
21.(1)证明：∵BE=EC，AF=FC，
∴EF//AB，AB=2EF，
∵AB=2AD，
∴AD=EF，AD/​/EF，
∴四边形ADFE是平行四边形，
∴AF与DE互相平分．
(2)解：在Rt△ABC中，∵∠BAC=90°，AB=6，BC=10，
∴AC= 102−62=8，
∵EF=12AB=3，
∴OA=OF=14QC=2，
∴OD=OE= 32+22= 13．
22.解：(1)设直线AB解析式为y=kx+b，把点A(52,2)，B(4,0)代入得52k+b=24k+b=0，
解得k=−43b=163，
∴直线AB解析式为y=−43x+163．
(2)如图1中，

①当AB=AC时，点C坐标(1,0)．
②当BC′=BA或BC″=BA时，
∵AB= 22+(32)2=52，
∴点C′(132,0)，C″(32,0)，
综上所述，当△ABC是以线段AB为腰的等腰三角形时，点C坐标为(1,0)或(132,0)或(32,0)．
(3)如图2中，存在．

①当AB为平行四边形的边时，P1(32,0)，Q1(0,2)或P3(−32,0)，Q3(0,−2)．
②当AB为平行四边形的对角线时，P2(132,0)，Q2(0,2)．
23.(1)证明：如图1，
∵四边形ABCD为正方形，
∴AB=AD，∠B=∠ADN=∠BAD=90°，
∵∠MAN=45°，
∴∠BAM+∠DAN=90°−45°=45°，
由题意得：△ABM≌△ADM′，
∴∠ADM′=∠B=90°，∠DAM′=∠BAM，AM=AM′，
∴∠ADN+∠ADM′=180°，
∴N，D，M′三点共线，
∵∠NAM′=∠DAN+∠DAM′=45°=∠MAN，
∵AN=AN，
∴△MAN≌△M′AN(SAS)，
∴MN=NM′，
∵NM′=DN+DM′，DM′=BM，
∴BM+DN=MN；
(2)解：猜想：BM+DN=MN，理由如下：
如图2，在MB的延长线上，截取BE=DN，连接AE，

在△ABE和△ADN中，
AB=AD∠ABE=∠DBE=DN，
∴△ABE≌△ADN(SAS)，
∴AE=AN，∠EAB=∠NAD，
∵∠BAD=90°，∠MAN=45°，
∴∠BAM+∠DAN=45°，
∴∠EAB+∠BAM=45°，
∴∠EAM=∠NAM，
同理得：△AEM≌△ANM(SAS)，
∴ME=MN，
又ME=BE+BM=BM+DN，
∴BM+DN=MN；
(3)解：DN−BM=MN，理由如下：
如图3，在DC上截取DF=BM，连接AF，

△ABM和△ADF中，
AB=AD∠ABM=∠DBM=DF，
∴△ABM≌△ADF(SAS)，
∴AM=AF，∠BAM=∠DAF，
∴∠BAM+∠BAF=∠BAF+∠DAF=90°，即∠MAF=∠BAD=90°，
∵∠MAN=45°，
∴∠MAN=∠FAN=45°，
在△MAN和△FAN中，
AM=AF∠MAN=∠FANAN=AN，
∴△MAN≌△FAN(SAS)，
∴MN=NF，
∴MN=DN−DF=DN−BM，
∴DN−BM=MN．
平行四边形的性质定理3平行四边形的对角线互相平分.我们可以用演绎推理证明这个结论．
已知：如图1，▱ABCD的对角线AC和BD相交于点O．
求证：OA=OC，OB=OD．