陕西省2024年中考数学试卷【附真题答案】

这是一份陕西省2024年中考数学试卷【附真题答案】，共11页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。

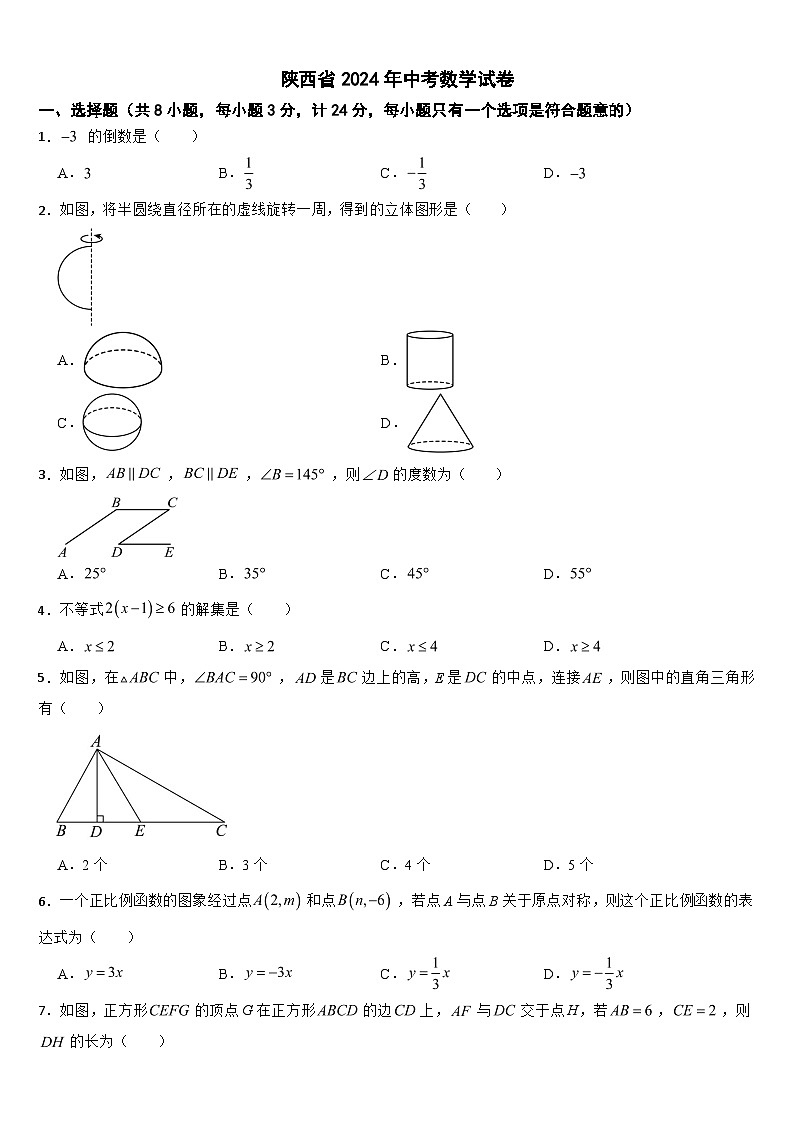
一、选择题（共8小题，每小题3分，计24分，每小题只有一个选项是符合题意的）
1． 的倒数是（ ）
A．B．C．D．
2．如图，将半圆绕直径所在的虚线旋转一周，得到的立体图形是（ ）
A．B．
C．D．
3．如图，，，，则的度数为（ ）
A．B．C．D．
4．不等式的解集是（ ）
A．B．C．D．
5．如图，在中，，是边上的高，E是的中点，连接，则图中的直角三角形有（ ）
A．2个B．3个C．4个D．5个
6．一个正比例函数的图象经过点和点，若点A与点B关于原点对称，则这个正比例函数的表达式为（ ）
A．B．C．D．
7．如图，正方形的顶点G在正方形的边上，与交于点H，若，，则的长为（ ）
A．2B．3C．D．
8．已知一个二次函数的自变量x与函数y的几组对应值如下表，
则下列关于这个二次函数的结论正确的是（ ）
A．图象的开口向上
B．当时，y的值随x的值增大而增大
C．图象经过第二、三、四象限
D．图象的对称轴是直线
二、填空题（共5小题，每小题3分，计15分）
9．分解因式： = ．
10．小华探究“幻方”时，提出了一个问题：如图，将0，，，1，2这五个数分别填在五个小正方形内，使横向三个数之和与纵向三个数之和相等，则填入中间位置的小正方形内的数可以是 ．（写出一个符合题意的数即可）
11．如图，是的弦，连接，，是所对的圆周角，则与的和的度数是 ．
12．已知点和点均在反比例函数的图象上，若，则 0．
13．如图，在中，，E是边上一点，连接，在右侧作，且，连接．若，，则四边形的面积为 ．
三、解答题（共13小题，计81分。解答题应写出过程）
14．计算：．
15．先化简，再求值：，其中，．
16．解方程：．
17．如图，已知直线l和l外一点A，请用尺规作图法，求作一个等腰直角，使得顶点B和顶点C都在直线l上．（作出符合题意的一个等腰直角三角形即可，保留作图痕迹，不写作法）
18．如图，四边形是矩形，点E和点F在边上，且．求证：．
19．一个不透明的袋子中共装有五个小球，其中3个红球，1个白球，1个黄球，这些小球除颜色外都相同．将袋中小球摇匀，从中随机摸出一个小球记下颜色后放回，记作随机摸球一次．
（1）随机摸球10次，其中摸出黄球3次，则这10次摸球中，摸出黄球的频率是 ．
（2）随机摸球2次，用画树状图或列表的方法，求这两次摸出的小球都是红球的概率．
20．星期天，妈妈做饭，小峰和爸爸进行一次家庭卫生大扫除．根据这次大扫除的任务量，若小峰单独完成，需；若爸爸单独完成，需．当天，小峰先单独打扫了一段时间后，去参加篮球训练，接着由爸爸单独完成剩余的打扫任务．小峰和爸爸这次一共打扫了，求这次小峰打扫了多长时间．
21．如图所示，一座小山顶的水平观景台的海拔高度为，小明想利用这个观景台测量对面山顶C点处的海拔高度，他在该观景台上选定了一点A，在点A处测得C点的仰角，再在上选一点B，在点B处测得C点的仰角，．求山顶C点处的海拔高度．（小明身高忽略不计，参考数据：，，）
22．我国新能源汽车快速健康发展，续航里程不断提升，王师傅驾驶一辆纯电动汽车从A市前往B市，他驾车从A市一高速公路入口驶入时，该车的剩余电量是，行驶了后，从B市一高速公路出口驶出，已知该车在高速公路上行驶的过程中，剩余电量与行驶路程之间的关系如图所示．
（1）求y与x之间的关系式；
（2）已知这辆车的“满电量”为，求王师傅驾车从B市这一高速公路出口驶出时，该车的剩余电量占“满电量”的百分之多少．
23．水资源问题是全球关注的热点，节约用水已成为全民共识．某校课外兴趣小组想了解居民家庭用水情况，他们从一小区随机抽取了30户家庭，收集了这30户家庭去年7月份的用水量，并对这30个数据进行整理，绘制了如下统计图表：
根据以上信息，解答下列问：
（1）这30个数据的中位数落在 组（填组别）；
（2）求这30户家庭去年7月份的总用水量；
（3）该小区有1000户家庭，若每户家庭今年7月份的用水量都比去年7月份各自家庭的用水量节约，请估计这1000户家庭今年7月份的总用水量比去年7月份的总用水量节约多少?
24．如图，直线l与相切于点A，是的直径，点C，D在l上，且位于点A两侧，连接，分别与交于点E，F，连接．
（1）求证：；
（2）若的半径，，，求的长．
25．一条河上横跨着一座宏伟壮观的悬索桥．桥梁的缆索与缆索均呈抛物线型，桥塔与桥塔均垂直于桥面，如图所示，以O为原点，以直线为x轴，以桥塔所在直线为y轴，建立平面直角坐标系．
已知：缆索所在抛物线与缆索所在抛物线关于y轴对称，桥塔与桥塔之间的距离，，缆索的最低点P到的距离（桥塔的粗细忽略不计）
（1）求缆索所在抛物线的函数表达式；
（2）点E在缆索上，，且，，求的长．
26．
（1）问题提出
如图1，在中，，，作的外接圆．则的长为 ；（结果保留π）
（2）问题解决
如图2所示，道路的一侧是湿地．某生态研究所在湿地上建有观测点D，E，C，线段和为观测步道，其中点A和点B为观测步道出入口，已知点E在上，且，，，，，现要在湿地上修建一个新观测点P，使．再在线段上选一个新的步道出入口点F，并修通三条新步道，使新步道经过观测点E，并将五边形的面积平分．
请问：是否存在满足要求的点P和点F?若存在，求此时的长；若不存在，请说明理由．（点A，B，C，P，D在同一平面内，道路与观测步道的宽、观测点及出入口的大小均忽略不计，结果保留根号）
答案
1．【答案】C
2．【答案】C
3．【答案】B
4．【答案】D
5．【答案】C
6．【答案】A
7．【答案】B
8．【答案】D
9．【答案】a（a﹣b）
10．【答案】0
11．【答案】
12．【答案】
13．【答案】60
14．【答案】解：.
15．【答案】解：
将，代入原式得.
16．【答案】解：，
方程两边同乘以得，
2+x(x+1)=
解得x=-3，
检验，当x=-3时，，
∴原方程的解为x=-3.
17．【答案】解：如图所示，△ABC为所求.
18．【答案】证明：∵四边形ABCD是矩形，
∴AB=CD，∠B=∠C=90°，
又∵BE=CF，BF=BC-CF，CE=BC-BE，
∴CE=BF，
∴△ABF≌△DCE(SAS)
∴AF=DF.
19．【答案】（1）0.3
（2）解：依题意，树状图如图所示，
其中，事件包含的可能结果为25个，符合题意的事件有9个，
∴.
20．【答案】解：设小峰打扫了x h，则爸爸打扫了(3-x) h，
依题意，，
解得x=2，
答：小峰打扫了．
21．【答案】解：如图所示，过点C作CD⊥AB交AB延长线于点D，
依题意得，∠CAE=42°，∠CBD=45°，AB=10，
∴∠BCD=180°-∠D-∠CBD=45°，
∴CD=BD，
设BD=CD=x，则AD=AB+BD=x+10
有，即，
解得x≈90.
∴山顶C处的海拔高度=90+1600=1690.
答：山顶C点处的海拔高度为．
22．【答案】（1）解：设直线关系式为y=kx+b，
依题意得，函数经过(150，50)和(0，80)
∴，解得.
∴y与x之间的关系式为；
（2）解：当x=240 km时，y=-0.2×240+80=32（ ），
∴.
答：该车的剩余电量占“满电量”的．
23．【答案】（1）B
（2）解：总用水量=5.3×10+8.0×12+12.5×6+15.5×2=53+96+75+31=255（m3）.
答： 这30户家庭去年7月份的总用水量.
（3）解：（m3）；
答： 这1000户家庭今年7月份的总用水量比去年7月份的总用水量节约.
24．【答案】（1）证明：∵AB是的直径 ，
∴∠AFB=90°，
∴∠BAF+∠ABF=180°-∠AFB=90°，
又∵ 直线l与相切于点A，
∴∠BAD=90°，
同理，∠ABF+∠ADB=180°-∠BAD=90°，
∴∠BAF=∠CDB.
（2）解：由（1）得，
在Rt△BAD和Rt△BAC中，
∵AB=2r=12，AC=12，AD=9，
∴CD=AC+AD=12+9=21，
，
.
又∵AE⊥BC，
∴BE=CE=，
又∵
∴∠BEF=∠BAF，
由（1）得∠BAF=∠CDB.
∴∠BEF=∠BDC，
又∵∠CBD=∠FBE，
∴△BEF∽△BDC，
∴，即
解得：.
25．【答案】（1）解：∵OC=100，
由对称可知，OD=CD=50，
又∵PD=2，
设 缆索所在抛物线的函数表达为，经过点A(0，17)，
∴，解得：.
∴缆索所在抛物线的函数表达为；
（2）解： ∵缆索所在抛物线与缆索所在抛物线关于y轴对称，
∴L2为，
当EF=2.6时，即y=2.6时，，解得x=-40或x=-60，
此时E未达到最低点，故x=-40，
∴的长为．
26．【答案】（1）
（2）解：存在满足要求的点P和点F，此时的长为．
连接CD，构造符合题意的∠DPC=60°，其中PF经过点E，设PF交CD于点H，过点C作CG⊥PH，
∵∠DAB+∠ABC=60°+120°=180°，
∴AD∥BC，
又∵AD=BC=900，
∴四边形ABCD是平行四边形，
∴CD=AB=1200，CD∥AB，
∵ 新步道经过观测点E，
∴FP平分平行四边形ABCD，
∵PF将五边形的面积平分，
故PF也需平分△CDP的面积，
∴H是CD的中点，CH=DH=，
又∵AE=EC，即E也是AC的中点，
∴HE∥AD，即PF∥AD，
∴四边形AFHD也是平行四边形，
∴FH=AD=900，
∴∠BFH=∠BAD=60°，∠CHP=∠BFH=60°，
又∵∠DPC=60°，∠DCP=∠PCD，
∴△CPH∽△CDP，
∴，即，
在Rt△CGH中，
∠HCG=180°-∠CGH-∠CHG=30°，
∴HG=，
∴，
∴，
∴PF=FH+GH+PG=1200+.x
…
0
3
5
…
y
…
0
…
组别
用水量
组内平均数
A
B
C
D