初中数学北师大版八年级上册3 平行线的判定说课课件ppt

这是一份初中数学北师大版八年级上册3 平行线的判定说课课件ppt，共27页。PPT课件主要包含了课前预习，课前导入，典例讲练等内容，欢迎下载使用。
数学 九年级上册 BS版
数学 八年级上册 BS版
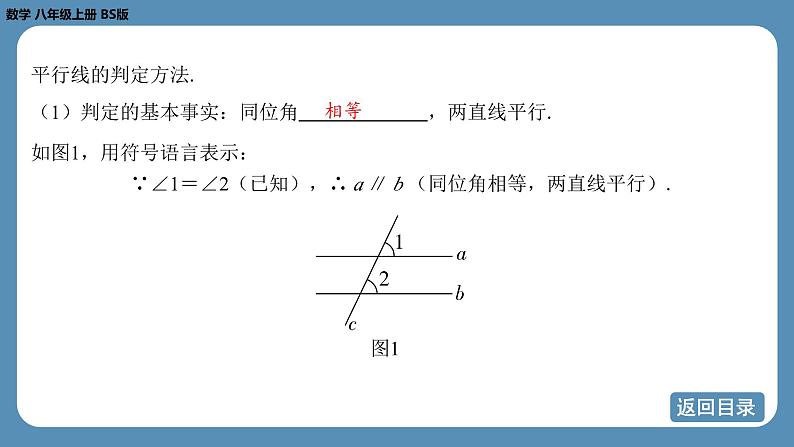
（1）判定的基本事实：同位角 ，两直线平行.
如图1，用符号语言表示： ∵∠1＝∠2（已知），∴ a ∥ b （同位角相等，两直线平行）.
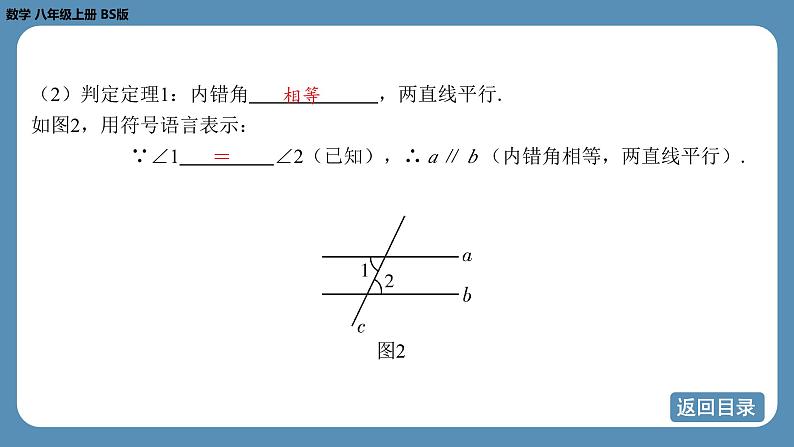
（2）判定定理1：内错角 ，两直线平行.如图2，用符号语言表示： ∵∠1 ∠2（已知），∴ a ∥ b （内错角相等，两直线平行）.
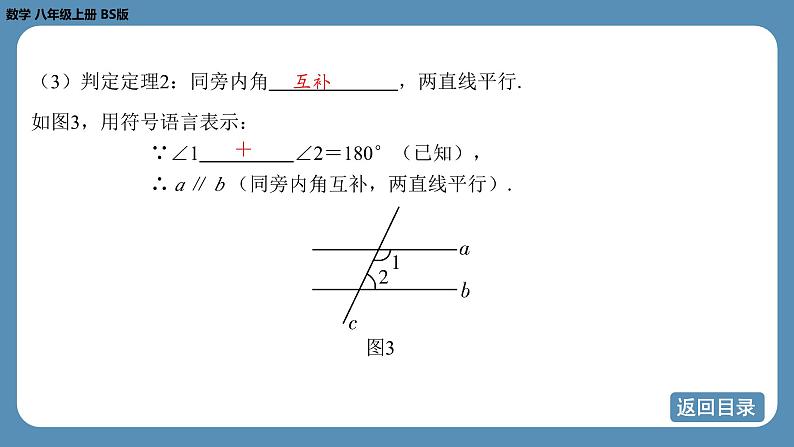
（3）判定定理2：同旁内角 ，两直线平行.
如图3，用符号语言表示： ∵∠1 ∠2＝180°（已知）， ∴ a ∥ b （同旁内角互补，两直线平行）.
（4）推论：在同一平面内，垂直于同一直线的两条直线 ⁠ ⁠.如图4，用符号语言表示： ∵ a ⊥ b ， b ⊥ c （已知）， ∴ （在同一平面内，垂直于同一直线的两条直线平行）.
请找出图中的平行线！它们为什么平行?
基本事实：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.
简单说成：同位角相等，两直线平行.
据说，人类知识的 75% 是在操作中学到的.小明用下面的方法作出平行线，你认为他的作法对吗？为什么？
通过这个操作活动，得到了什么结论?
定理 两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.
这个定理可以简单说成：内错角相等，两直线平行.
如图，∠1 和∠2 是直线 a，b 被直线 c 截出的内错角，且∠1 =∠2. 求证：a∥b.
证明：∵∠1 =∠2 (已知)，∠1 =∠3 (对顶角相等)，∴∠2 =∠3 (等量代换).∴ a∥b (同位角相等，两直线平行).
判定方法2：两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.
简单说成：内错角相等，两直线平行.
∵∠3 =∠2(已知)，∴ a∥b (内错角相等，两直线平行).
证明：∵∠1 与∠2 互补 (已知)，∴∠1 +∠2 = 180° (互补的定义).又∵∠3 +∠2 = 180° (平角的定义)，∴∠1 =∠3 (同角的补角相等). ∴ a∥b (同位角相等，两直线平行).
如图，∠1 和∠2 是直线 a、b 被直线 c 截出的同旁内角，且∠1 与∠2 互补. 求证：a∥b.
判定方法3：两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.
简单说成：同旁内角互补，两直线平行.
∵∠1 +∠2 = 180° (已知)，∴ a∥b (同旁内角互补，两直线平行).
（1）如图，在下列条件中，可得到 AD ∥ BC 的是（　C　）① AC ⊥ AD ， AC ⊥ BC ；②∠1＝∠2，∠3＝∠ D ；③∠4＝∠5；④∠ BAD ＋∠ ABC ＝180°.
【解析】①∵ AC ⊥ AD ， AC ⊥ BC ，∴∠ DAC ＝∠ ACB ＝90°.∴ AD ∥ BC . 故①符合题意；②∵∠1＝∠2，∴ BC ∥ EF . ∵∠3＝∠ D ，∴ AD ∥ EF . ∴ AD ∥ BC . 故②符合题意； ③∵∠4＝∠5，∴ AB ∥ CD ，不能得到 AD ∥ BC . 故③不符合题意；④∵∠ BAD ＋∠ ABC ＝180°，∴ AD ∥ BC . 故④符合题意.综上所述，能判定 AD ∥ BC 的有①②④.故选C.
（2）如图，①由∠1＝ ，能得到 ED ∥ BC ；②由∠ C ＝ ，能得到 ED ∥ BC ；③由∠4＝ ，能得到 ED ∥ BC ；④由∠5与 互补，能得到 ED ∥ BC ；⑤由∠ C 与 互补，能得到 ED ∥ BC .
【解析】①∠1与∠2是内错角，由∠1＝∠2，能得到 ED ∥ BC ；②∠ C 与∠3是同位角，由∠ C ＝∠3，能得到 ED ∥ BC ；③∠ ABC 与∠4是同位角，由∠4＝∠ ABC ，能得到 ED ∥ BC ；④∠5与∠ ABC 是同旁内角，由∠5与∠ ABC 互补，能得到 ED ∥ BC ；⑤∠ C 与∠ EDC 是同旁内角，由∠ C 与∠ EDC 互补，能得到 ED ∥ BC . 故答案为∠2，∠3，∠ ABC ，∠ ABC ，∠ EDC .
【点拨】证明两直线平行时，一定要弄清是哪两条直线被哪一条直线所截形成同位角、内错角、同旁内角，再进一步判断有无相等或互补关系.在“三线八角”图中，同位角相等、内错角相等、同旁内角互补，只需其中一个结论成立，则利用对顶角、邻补角等相关知识，可得到另两个结论也成立.
1. 对于图中标记的各角，下列条件能够推理得到 a ∥ b 的是（　D　）
2. 如图，请添加一个条件 ⁠，使得 AB ∥ CD .
∠ BEF ＝∠ C （答案不唯一）　
如图，已知∠1＋∠2＝180°，求证：∠3＝∠4.
证明：∵∠2＝∠5（对顶角相等），∠1＋∠2＝180°（已知），∴∠1＋∠5＝180°（等量代换）.∴ CD ∥ EF （同旁内角互补，两直线平行）.∴∠3＝∠4（两直线平行，同位角相等）.
【点拨】此题考查了平行线的判定定理和性质定理，根据已知条件找到同位角相等或内错角相等或同旁内角互补是解题的关键.
如图，已知直线 AB ， CD 被直线 EO 所截，且∠ EMB ＝∠ MND ， MG 平分∠EMB ， NF 平分∠ MND . 求证： MG ∥ NF .
已知四边形 ABCD 是长方形. （1）如图1，若 CD ＝3， BC ＝4， AE ⊥ BD 于点 E ，点 P 是 BD 上的一动点，连接 CP . 当 CP 为何值时， CP ∥ AE ？ 请说明理由.
（2）当∠ BAP ＝57.5°时， AE ∥ BD . 理由如下：设∠ BAP ＝ x ，则∠ EAP ＝∠ BAP ＝ x . 要使 AE ∥ BD ，则∠ EAD ＝∠ ADB ＝25°，此时∠ DAP ＝∠ PAE －∠ EAD ＝ x －25°.又∵∠ BAD ＝∠ BAP ＋∠ DAP ＝ x ＋ x －25°＝90°，∴ x ＝57.5°.故当 ∠ BAP ＝57.5°时， AE ∥ BD .
【点拨】在判定两直线平行时，要注意两点：（1）以截线为线索找准同位角、内错角或同旁内角；（2）不要用错或用混判定条件.
（2）如图2，若∠ ADB ＝25°，点 P 为 BC 边上的一动点，将△ ABP 沿 AP 翻折到△ AEP 位置.当∠ BAP 等于多少度时， AE ∥ BD ？ 请说明理由.
如图，将一副三角板中的两个直角顶点 C 叠放在一起，其中∠ ACB ＝∠ DCE ＝90°，∠ A ＝30°，∠ B ＝60°，∠ D ＝∠ E ＝45°.设∠ ACE ＝ x .（1）填空：∠ BCE ＝ ，∠ ACD ＝ ⁠； （用含 x 的代数式表示）（2）若∠ BCD ＝5∠ ACE ，求∠ ACE 的度数；
（1）【解析】由题意可知，∠ BCE ＝∠ ACB －∠ ACE ＝90°－ x ，∠ ACD ＝∠ DCE －∠ ACE ＝90°－ x .故答案为90°－ x ，90°－ x .
（2）解：∵∠ BCD ＝∠ ACB ＋∠ ACD ＝90°＋∠ ACD ，∴∠ BCD ＝90°＋（90°－ x ）＝180°－ x .∵∠ BCD ＝5∠ ACE ，∴180°－ x ＝5 x ，解得 x ＝30°.∴∠ ACE ＝30°.
（3）若三角板 ABC 不动，三角板 DCE 绕顶点 C 转动，则当∠ BCE 等于多少度时， CD ∥ AB ？
（3）解：要使 CD ∥ AB ，有以下两种情况：①如图1，当∠ BCD ＋∠ B ＝180°时， CD ∥ AB .∵∠ B ＝60°，∠ BCD ＝∠ DCE ＋∠ BCE ＝90°＋∠ BCE ， ∴（90°＋∠ BCE ）＋60°＝180°.∴∠ BCE ＝30°；②如图2，当∠ BCD ＝∠ B ＝60°时， CD ∥ AB . ∵∠ DCE ＝90°，∠ BCE ＝∠ BCD ＋∠ DCE ，∴∠ BCE ＝90°＋60°＝150°.综上所述，当∠ BCE 等于30°或150°时， CD ∥ AB .