初中数学第一章 特殊平行四边形3 正方形的性质与判定背景图课件ppt

这是一份初中数学第一章 特殊平行四边形3 正方形的性质与判定背景图课件ppt，共21页。PPT课件主要包含了课前预习，课前导入，典例讲练等内容，欢迎下载使用。
数学 九年级上册 BS版
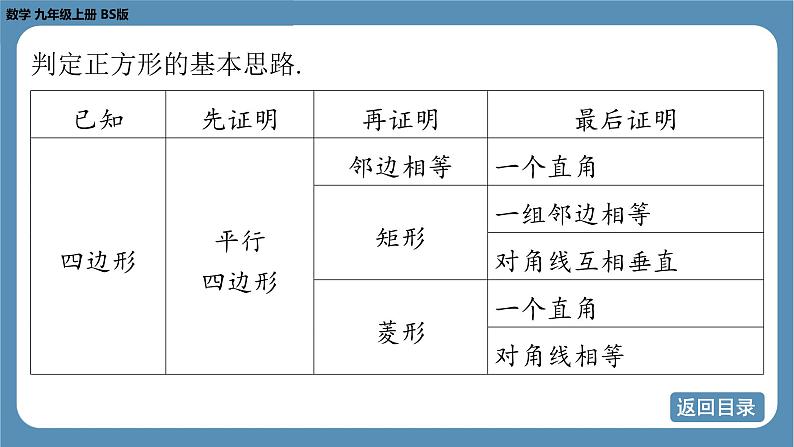
判定正方形的基本思路.
问题1 什么是正方形？正方形有哪些性质？
正方形：有一组邻边相等，并且有一个角是直角的平行四边形.
正方形性质：①四个角都是直角； ②四条边都相等； ③对角线相等且互相垂直平分.
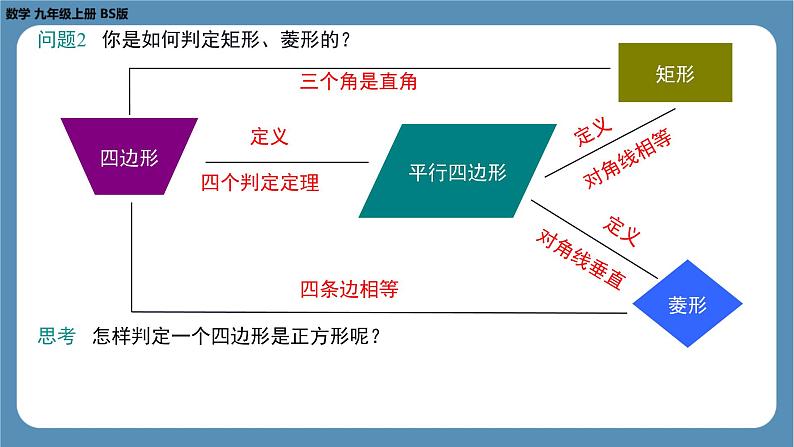
问题2 你是如何判定矩形、菱形的？
思考 怎样判定一个四边形是正方形呢？
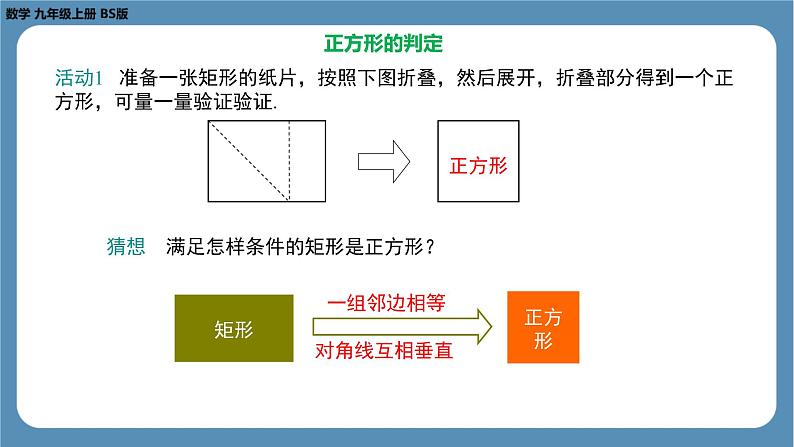
活动1 准备一张矩形的纸片，按照下图折叠，然后展开，折叠部分得到一个正方形，可量一量验证验证.
猜想 满足怎样条件的矩形是正方形？
已知：如图,在矩形 ABCD 中，AC，DB 是它的两条对角线，AC⊥DB.求证：四边形 ABCD 是正方形.证明：∵ 四边形 ABCD 是矩形，∴ AO = CO = BO = DO，∠ADC = 90°.∵ AC⊥DB，∴ AD = AB = BC = CD.∴ 四边形 ABCD 是正方形.
对角线互相垂直的矩形是正方形.
活动2 把可以活动的菱形框架的一个角变为直角，观察这时菱形框架的形状，量量看是不是正方形.
猜想 满足怎样条件的菱形是正方形？
已知：如图，在菱形 ABCD 中，对角线 AC = DB.求证：四边形 ABCD 是正方形.证明：∵ 四边形 ABCD 是菱形,∴ AB = BC = CD = AD，AC⊥DB.∵ AC = DB，∴ AO = BO = CO = DO.∴△AOD，△AOB，△COD，△BOC 是等腰直角三角形.∴∠DAB =∠ABC =∠BCD =∠ADC = 90°.∴ 四边形 ABCD 是正方形.
对角线相等的菱形是正方形.
正方形判定的几条途径：
在四边形 ABCD 中，已知 AC 与 BD 相交于点 O ，那么下列条件中能判定这个四边形是正方形的是（　C　）
【解析】A. 不能判定这个四边形是正方形，只能判定这个四边形是矩形；B. 不能判定这个四边形是正方形，只能判定这个四边形是平行四边形；C. 能判定这个四边形是正方形；D. 不能判定这个四边形是正方形，只能判定这个四边形是菱形.故选C.
【点拨】判定一个四边形为正方形的途径有三种：①先说明它是平行四边形，再说明有一组邻边相等，且有一个角是直角；②先说明它是矩形，再说明有一组邻边相等，或说明对角线互相垂直；③先说明它是菱形，再说明它有一个角是直角，或说明对角线相等.
如图，在菱形 ABCD 中，对角线 AC ， BD 相交于点 O ，添加下 列条件中的一个，则能使菱形 ABCD 成为正方形的是（　A　）
如图，在△ ABC 中，∠ ACB ＝90°，点 D 在 AB 边上且 AD ＝ BD ，连接 CD ，点 E 是 CD 的中点，过点 C 作 CF ∥ AB ，交 AE 的延长线于点 F ，连接 BF .
（1）求证： AE ＝ EF ；
（2）判断四边形 BDCF 的形状，并说明理由；
（2）解：四边形 BDCF 是菱形.理由如下：由（1）知，△ ADE ≌△ FCE ，∴ AD ＝ FC . ∵ AD ＝ BD ，∴ FC ＝ BD . ∵ CF ∥ BD ，∴四边形 BDCF 是平行四边形，∵∠ ACB ＝90°， AD ＝ BD ，∴ CD ＝ BD . ∴▱ BDCF 是菱形.
（3）当∠ ABC ＝45°时，直接判断四边形 BDCF 的形状.
（3）解：四边形 BDCF 是正方形.由（2）知， CD ＝ BD ，且∠ ABC ＝45°，∴∠ DCB ＝∠ DBC ＝45°.∴∠ BDC ＝90°.又∵四边形 BDCF 是菱形，∴菱形 BDCF 是正方形.
【点拨】正方形的判定思路通常有三个途径：（1）从定义去判定，先证明平行四边形，再证明一组邻边相等和一个角是直角；（2）先证明矩形，再证明一组邻边相等或对角线互相垂直；（3）先证明菱形，再证明一个角是直角或对角线相等.另外还要灵活运用全等三角形的判定和性质，直角三角形的性质和等腰三角形的性质等.
如图，在△ ABC 中，已知 BD 是△ ABC 的角平分线，过点 D 作 DE ∥ BC 交 AB 于点 E ， DF ∥ AB 交 BC 于点 F .
（1）求证：四边形 BEDF 是菱形；
（1）证明：∵ DE ∥ BC ， DF ∥ AB ，∴四边形 BEDF 是平行四边形，∠ EDB ＝∠ DBF . ∵ BD 平分∠ ABC ，∴∠ EBD ＝∠ DBF . ∴∠ EBD ＝∠ EDB . ∴ EB ＝ ED . ∴▱ BEDF 是菱形.
（2）若 AB ＝ BC 且 AC ＝2 BD ，试判断四边形 BEDF 的形状并说明理由.
如图，在△ ABC 中，已知 AB ＝ BC ，∠ ABC ＝90°，点 D 为边 BC 的中点，在 AC 上取一点 E ，使得∠ EDC ＝∠ ADB ，连接 BE 交 AD 于点 O . 求证： BE ⊥ AD .
证明：如图，过点 C 作 BC 的垂线交 DE 的延长线于点 F ，连接 AF .
∵点 D 为边 BC 的中点，
∴ BD ＝ CD .
又∵∠ EDC ＝∠ ADB ，∠ ABD ＝∠ FCD ＝90°，
∴△ ABD ≌△ FCD （ASA）.
∴ AB ＝ FC .
∵∠ ABD ＝∠ FCD ＝90°，
∴∠ ABC ＋∠ FCD ＝180°.
∴ AB ∥ CF .
∴四边形 ABCF 是平行四边形.
又∵∠ FCB ＝90°，
∴▱ ABCF 是矩形.
又∵ AB ＝ BC ，
∴矩形 ABCF 是正方形.
∴ BC ＝ CF ，∠ ACB ＝∠ ACF ＝45°.
又∵ EC ＝ EC ，
∴△ BCE ≌△ FCE （SAS）.
∴∠ CFE ＝∠ CBE .
又∵△ ABD ≌△ FCD ，
∴∠ BAD ＝∠ CFD . ∴∠ BAD ＝∠ CBE .
∵∠ BAD ＋∠ ADB ＝90°，
∴∠ CBE ＋∠ ADB ＝90°.
∴∠ BOD ＝90°.
∴ BE ⊥ AD .
【点拨】解决本题的关键是构建正方形 ABCF .
如图，在Rt△ ABC 中，∠ BAC ＝90°，点 D 是 BC 的中点，点 E 是 AD 的中点.过点 A 作 AF ∥ BC 交 BE 的延长线于点 F ，连接 CF .
（1）求证：△ AEF ≌△ DEB ；
（2）当△ ABC 满足什么条件时，四边形 ADCF 是正方形？请说明理由.