初中数学北师大版八年级上册第二章 实数6 实数课文配套ppt课件

这是一份初中数学北师大版八年级上册第二章 实数6 实数课文配套ppt课件，共23页。PPT课件主要包含了或－1等内容，欢迎下载使用。
1. 在下列实数中，属于有理数的是（　B　）
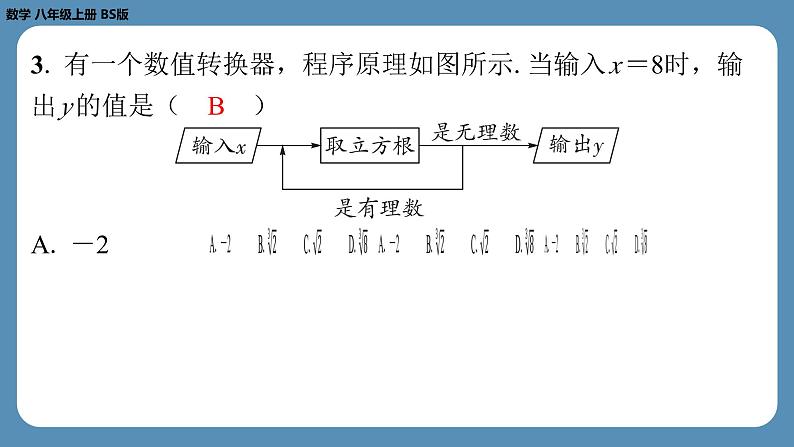
3. 有一个数值转换器，程序原理如图所示.当输入 x ＝8时，输 出 y 的值是（　B　）
（2）求 x 的值：9（3 x ＋1）2－49＝0.
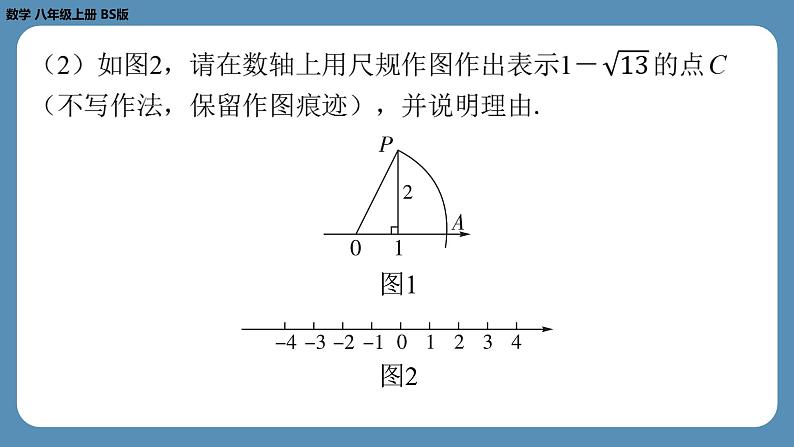
8. 我们知道，实数与数轴上的点一一对应，因此无理数也可以 在数轴上表示出来.（1）如图1，数轴上点 A 表示的数是 ⁠；
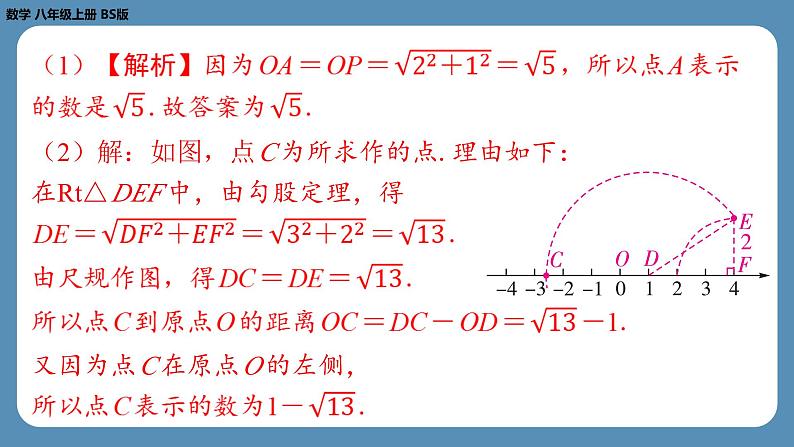
（2）解：如图，点 C 为所求作的点.理由如下：
在Rt△ DEF 中，由勾股定理，得
又因为点 C 在原点 O 的左侧，
（2）3 a － b ＋ c 的平方根.
（2）因为 a ＝3， b ＝－38， c ＝2，所以3 a － b ＋ c ＝3×3－（－38）＋2＝49.所以3 a － b ＋ c 的平方根是±7.
解：原式＝｜2－ a ｜＋｜ a －4｜，当 a ＜2时，原式＝（2－ a ）＋（4－ a ）＝6－2 a ＝2，解得 a ＝ 2（舍去）；当2≤ a ＜4时，原式＝（ a －2）＋（4－ a ）＝2，等式恒成 立；当 a ≥4时，原式＝（ a －2）＋（ a －4）＝2 a －6＝2，解 得 a ＝4.所以 a 的取值范围是2≤ a ≤4.
（1）【解析】因为2≤ a ≤5，所以 a －5≤0，2－ a ≤0.所以原 式＝｜ a －5｜＋｜2－ a ｜＝5－ a ＋ a －2＝3.故答案为3.
（2）解：由题意，得｜ a －3｜＋｜ a ＋4｜＝7.当 a ＜－4时， a －3＜0， a ＋4＜0，所以原式化为3－ a －（ a ＋4）＝7，解得 a ＝－4（舍去）；当－4≤ a ≤3时， a －3≤0， a ＋4≥0，所以原式化为3－ a ＋（ a ＋4）＝7，等式恒成立；当 a ＞3时， a －3＞0， a ＋4＞0，所以原式化为 a －3＋（ a ＋4）＝7，解得 a ＝3（舍去）.综上所述， a 的取值范围是－4≤ a ≤3.
（3）解：原式可化为｜ a ＋1｜＋｜ a －2｜＝5.当 a ＜－1时， a ＋1＜0， a －2＜0，所以原式化为－（ a ＋1）＋（2－ a ）＝5，
解得 a ＝－2；当－1≤ a ＜2时， a ＋1≥0， a －2＜0，所以原式化为 a ＋1＋（2－ a ）＝5，无解；当 a ≥2时， a ＋1＞0， a －2≥0，所以原式化为 a ＋1＋（ a －2）＝5，解得 a ＝3.综上所述， a ＝－2或 a ＝3.